Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

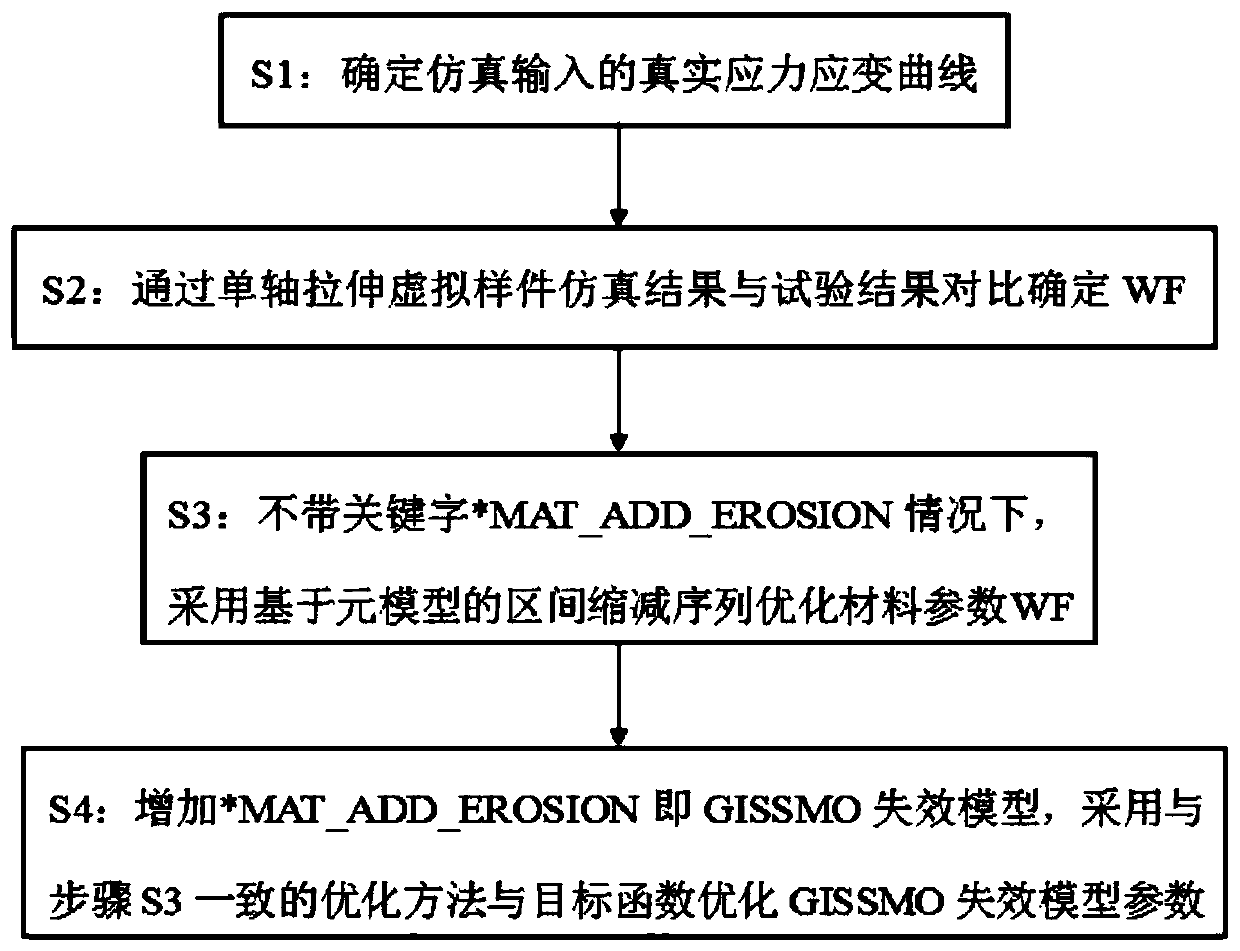
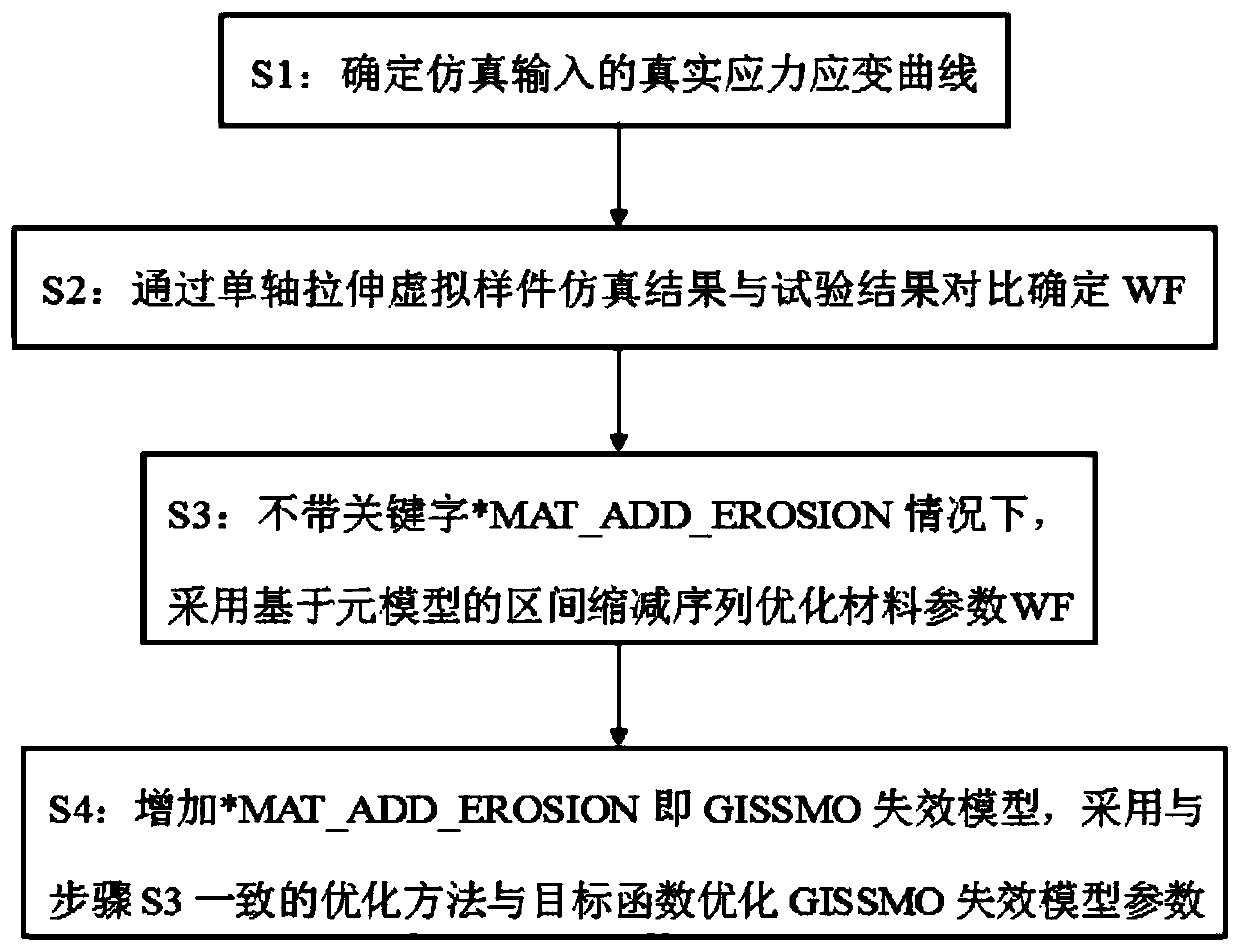
GISSMO material failure model parameter optimization method

An optimization method and technology of model parameters, applied in the field of materials, can solve problems such as large amount of calculation, difficult to obtain optimal solutions, etc., to achieve the effect of reducing workload and easy optimal solutions

Active Publication Date: 2020-05-08
CHINA AUTOMOTIVE ENG RES INST +1
View PDF7 Cites 12 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The invention provides a GISSMO material failure model parameter optimization method, which solves the traditional technical problems of large amount of calculation and difficulty in obtaining the optimal solution when calibrating model parameters with the help of experimental results

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • GISSMO material failure model parameter optimization method
  • GISSMO material failure model parameter optimization method
  • GISSMO material failure model parameter optimization method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0020] The fracture failure mechanism of metal materials can be divided into normal fracture, shear fracture and instability failure. Normal fracture is caused by the formation and combination of internal pores during metal deformation, and its fracture morphology is relatively rough; while shear fracture is caused by shear band slippage, and its fracture morphology is relatively smooth. The GISSMO failure model provides a phenomenological equation for the description of material fracture behavior. Assuming that the stressed section contains some micro-defects in the S area, the actual effective area of ​​​​the section is The damage parameter D is introduced into the constitutive equation, and the damage coefficient can be expressed as:

[0021]

[0022] The reduction of the section in the effective area brings about the dilution of the section stiffness, and the actual stress value is corrected as:

[0023] σ * =σ(1-D) (2)

[0024] The GISSMO failure model describes th...

Embodiment 2

[0053] Compared with Example 1, the only difference is that when the proportional loading method is adopted, the nonlinear accumulation of DMGEXP increases is a concave function, and the greater the DMGEXP before fracture, the greater the damage accumulation, the slower the front end and the slower the rear end block. When DMGEXP is 2.0, 2.2, 2.4, and 2.6 respectively, the engineering stress-strain curve slightly delays fracture with the increase of DMGEXP. The increase of DMGEXP is slightly delayed in engineering stress-strain curve. When DMGEXP=2, the non-linear damage accumulation is more consistent with the test results. In order to reduce the degree of nonlinearity of the optimization model, DMGEXP can take 2.

Embodiment 3

[0055] The only difference from Example 2 is that when using Metamodel-based optimization to fit the sampling points and output the functional relationship between the response variable Y and a set of input variables (X1, X2...Xn), it does not directly input Instead, two curves Lm and LM are fitted first, and then a region is formed between Lm and LM, and a certain curve LR is selected between the regions, and this curve LR is used as the test target engineering stress-strain curve.

[0056] Since the measured sampling point data will have certain errors, the actual value of the sampling point must be in a certain value range Xim≤Xi≤XiM, Yim≤Yi≤YiM. That is, Xi ∈ [Xim, XiM], Xim is the minimum value of Xi collected during the experiment, XiM is the maximum value of Xi collected during the experiment; Yi ∈ [Yim, YiM], Yim is the Yi collected during the experiment The minimum value of YiM is the maximum value of Yi collected during the experiment; i=1, 2, 3...n. Therefore, if t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to the technical field of materials, in particular to a GISSMO material failure model parameter optimization method which comprises the following steps: S1, determining a real stress-strain curve of simulation input; s2, comparing the simulation result of the uniaxial stretching virtual sample with the test result to determine the initial range of the WF; s3, under the condition that no keyword * MAT_ADD _ EROSION exists, optimizing the material parameter WF by adopting an interval reduction sequence based on a meta-model; and S4, adding * MATs _ ADD _ EROSION, namely a GISSMO failure model, and optimizing GISSMO failure model parameters by adopting an optimization method consistent with the step S3 and a target function. According to the method, based on a GISSMO failure model provided in commercial finite element software LS-DYNA, GISSMO failure model parameters are reversely solved and calibrated according to material mechanical property test data parameters; by adopting the LS-OPT, material parameters can be quickly identified, so that output engineering stress-strain curves of simulation and test can obtain relatively good consistency, and a reference canbe provided for establishment of a quick, automatic and high-precision failure material library.

Description

technical field [0001] The invention relates to the field of material technology, in particular to a parameter optimization method of a GISSMO material failure model. Background technique [0002] The application proportion of high-strength steel in automobiles continues to expand, but the increase in strength leads to a decrease in the ductility of the material, which makes it prone to fracture in certain collision conditions. Traditional crashworthiness simulation analysis is more maturely applied to the development of body structure, but its accuracy still needs to be improved. In this regard, the document CN106096259B discloses a material failure analysis method, which includes the following steps: obtaining the failure background of the failure part; performing visual inspection on the failure part to obtain the failure information of the failure part; Background and / or material failure data matched with the failure information to obtain the estimated failure cause of ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/23G06F30/17G01N3/08G06F111/10G06F119/14
CPCG01N3/08G01N2203/0212
Inventor 何恩泽赵清江周佳史爱民赵岩梁宾郭怡晖
Owner CHINA AUTOMOTIVE ENG RES INST
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com