Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Truss structure deformation decomposition method based on orthogonal theory

A truss structure and deformation decomposition technology, applied in the field of mechanical analysis, can solve the problems that the deformation decomposition method has not yet been discovered

Active Publication Date: 2020-04-21
ZHENGZHOU UNIV
View PDF7 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

At present, no deformation decomposition method for truss structures based on orthogonal theory has been found

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Truss structure deformation decomposition method based on orthogonal theory
  • Truss structure deformation decomposition method based on orthogonal theory
  • Truss structure deformation decomposition method based on orthogonal theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

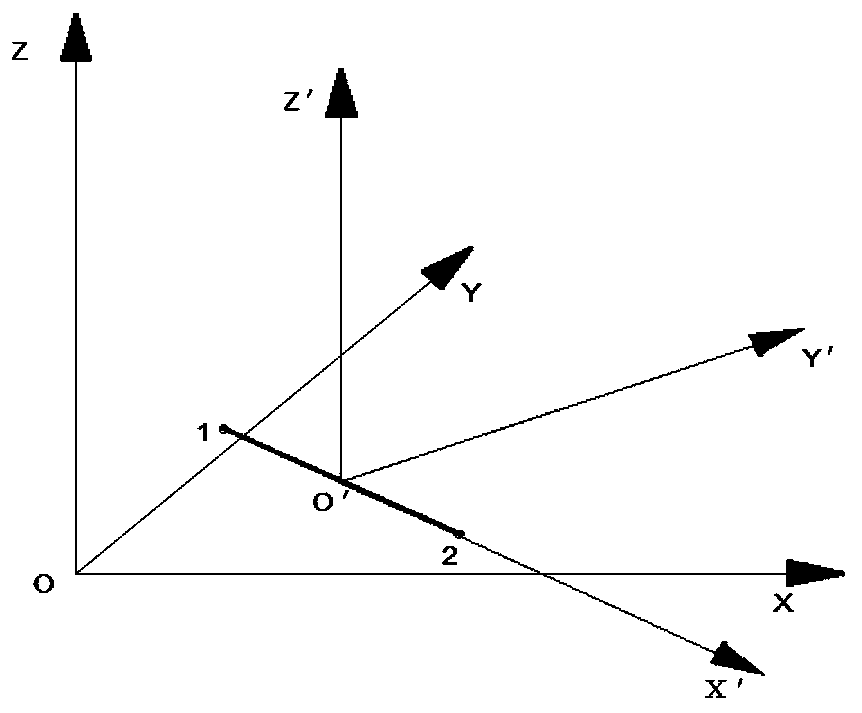
[0125] Embodiment one below in conjunction with appendix Figure 10 The specific implementation of the present invention will be described in detail.

[0126] Such as Figure 10 As shown, taking a vertical truss hinged at the bottom as an example, the length and width of the bottom of the truss are 0.2m, the height of the truss is 0.6m, the length and width of the bottom are the X axis and the Y axis, and the height direction is the Z axis. The elastic modulus of the truss structure is 3030Mpa, the Poisson's ratio is 0.2, and the radius of the rod element is 10mm. A load of 500N in the X direction is applied to the two nodes on the top of the truss respectively. Select the three vertical bar units of the truss and mark them as No. 1, No. 2, and No. 3 bar units, respectively, and decompose the deformation of the three bars respectively.

[0127] Through the force calculation of the truss structure, the displacement of each node of the truss structure can be obtained, and the...

Embodiment 2

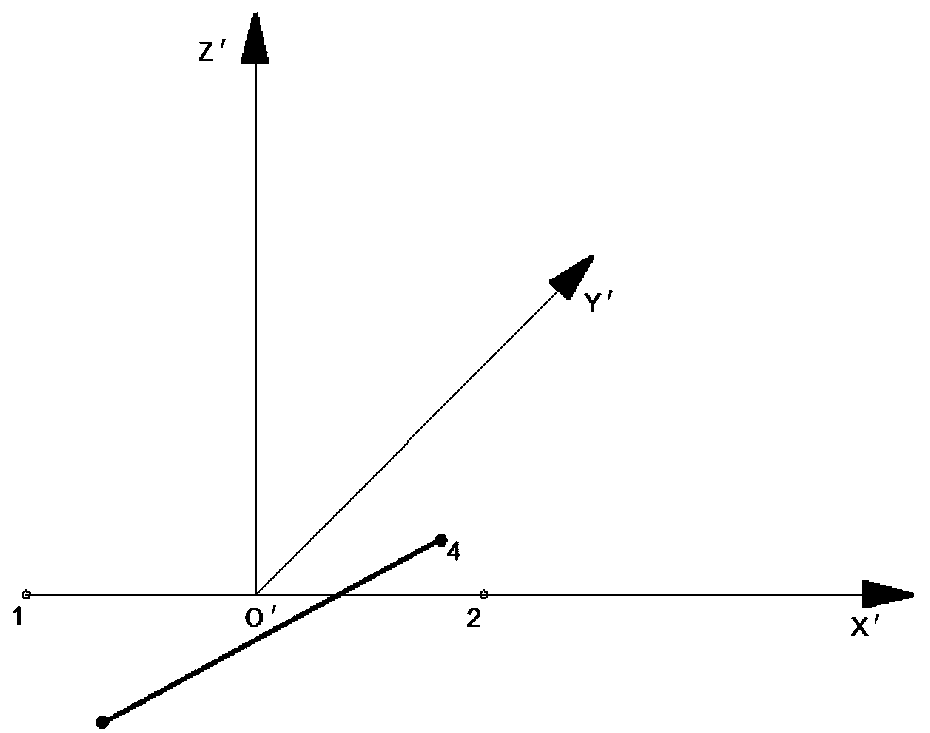
[0156] Attached below Figure 12 The No. 4 oblique rod in the structural column of the central gantry frame is decomposed by deformation.

[0157] Such as Figure 12 As shown, the gantry structure is 6 meters high, 22.5 meters wide, the diameter of the main truss of the beam is 9.58cm, the diameter of the main truss in the column is 11.2cm, the diameter of the oblique rod is 7.98cm, and the elastic modulus of the rod is 206000N / mm , with a density of 7.8×10 -6 . The bottom of the gantry is hinged.

[0158] Through the modal analysis of the gantry structure, it can be obtained that the node coordinate displacement vector d of the gantry structure in the local coordinate system of the No. e for:

[0159] d e =(-0.0136, 0.0034, 0.0586, -0.009, 0.0048, 0.01).

[0160] Through calculation, the projection coefficients and proportions of each basic displacement of the No. 4 rod unit in the local coordinate system are shown in Table 7. In the local coordinate system, the linea...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the technical field of mechanical analysis, and discloses a truss structure deformation decomposition method based on an orthogonal theory, which comprises the following stepsof: firstly, obtaining a complete orthogonal mechanical basis matrix under a local coordinate system by adopting an orthogonal theory decomposition method; projecting the coordinate displacement vector of each rod unit node of the truss structure under the local coordinate system onto a complete orthogonal mechanical basis matrix, and obtaining a projection coefficient vector of a rod unit underthe local coordinate system through linear transformation; converting the basic displacement projection coefficient vector under a local coordinate system into a basic displacement projection coefficient vector under an overall coordinate system through space coordinate transformation; and judging basic displacement information and deformation information of the rod unit according to the basic displacement and deformation projection coefficient vectors under the local and overall coordinate systems. According to the method, the basic displacement and deformation information in the comprehensive deformation of the truss structure can be visually and quickly quantified and identified.

Description

technical field [0001] The invention belongs to the technical field of mechanical analysis, and relates to a deformation decomposition method of a truss structure based on an orthogonal theory. Background technique [0002] The truss structure is widely used in various engineering structures, such as truss bridges, stadiums, and transfer floors of high-rise buildings, due to its advantages of saving materials and achieving large spans. In an ideal state, each bar unit of the truss is only subjected to axial force, the cross-sectional stress distribution is uniform, and each part of the truss bar unit can reach the stress allowable value at the same time, so the truss structure is an ideal structural form. However, safety accidents of truss structures have emerged in an endless stream in recent years. This is because the displacement deformation of truss structures under load conditions is still a comprehensive deformation. The existing analysis methods cannot directly identi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F30/13G06F30/20G06F119/14
Inventor 王东炜尚孟飞孙攀旭赵瑞青吴垒
Owner ZHENGZHOU UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com