Guidance tool error identification method based on particle swarm optimization algorithm
A particle swarm algorithm and identification method technology, which is applied in the field of guidance tool error identification based on particle swarm algorithm, can solve the problems of many human factors, large amount of calculation, and low trajectory reproduction accuracy
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
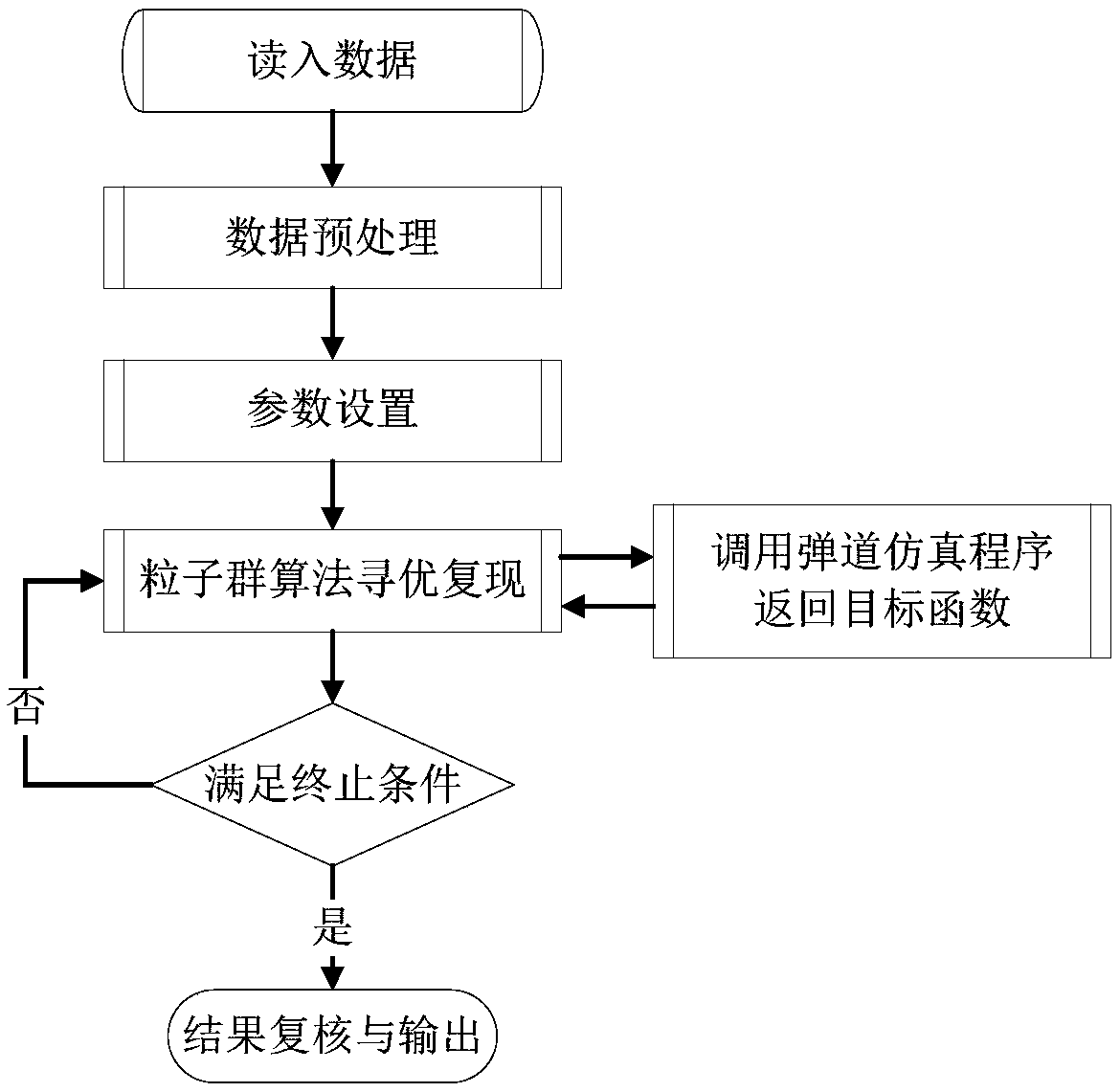
[0056] see figure 1 , a guidance tool error identification method based on particle swarm optimization, including the following steps:
[0057] Step 1. Obtain data information;
[0058] Step 2. Preprocessing the data information obtained in Step 1;
[0059] Step 3. Set parameters;
[0060] Step 4, identify the guidance error coefficient by the particle swarm algorithm (specifically, the particle swarm algorithm optimization and reproduction), wherein: during the identification process, each particle will call the ballistic simulation program and return the objective function;
[0061] Step 5. If the termination condition is met, then perform a result review and output the identification result of the error coefficient of the guidance tool; otherwise, return to Step 4.
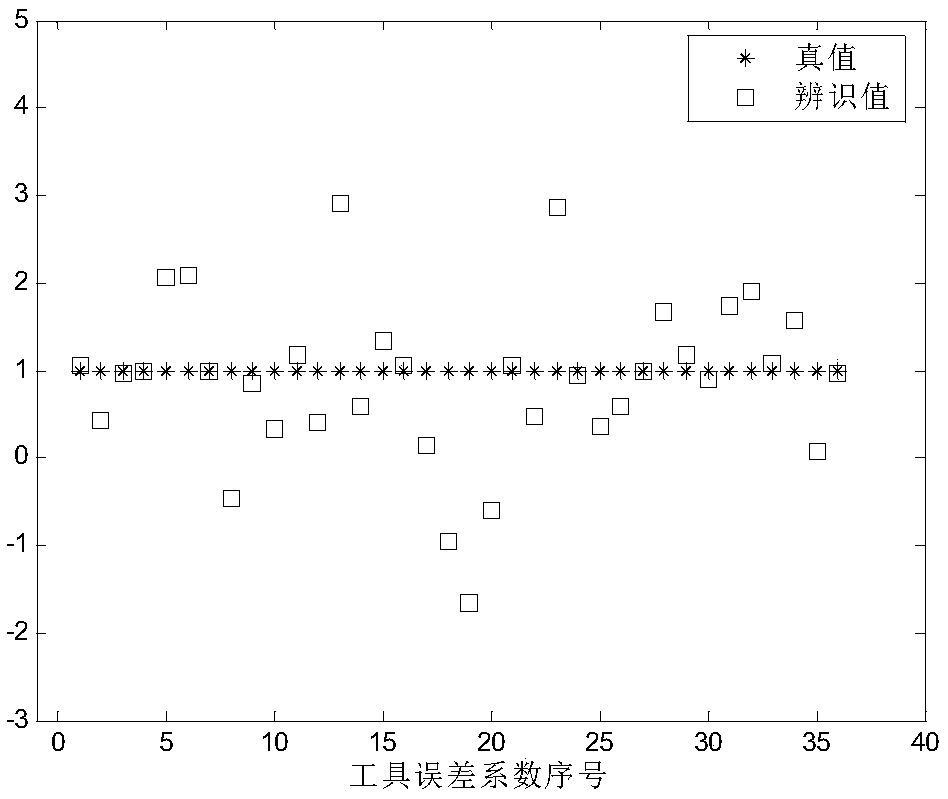
[0062] The data acquired in the above step 1 includes flight trajectory data, pre-test information data and landing point deviation data. Among them, the flight trajectory data includes the telemetry and ex...
Embodiment 2
[0127] Embodiment 2 differs from Embodiment 1 only in that: the weighted residual error of the landing point deviation fitting is incorporated into the objective function, and the new composite objective function after the combination is set as expression 4):
[0128]
[0129] Where: F 合 is the composite objective function; F is the sum of the sum of the squares of the apparent velocity heterodyne fitting residuals of the sampling points in each direction; ΔL is the longitudinal deviation of the landing point; ΔH is the horizontal deviation of the landing point; j is the error coefficient of the j-th guidance tool, is the error coefficient k of the guidance tool for the j-th item of the longitudinal deviation of the landing point j partial derivative of is the error coefficient k of the guidance tool for the j-th item traverse deviation of the landing point j Partial derivative of , j=1,2,...M; ω 1 is the weighting coefficient of the trajectory of the active segment; ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com