Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Interharmonic detection method based on polynomial fitting and non-interference area division

A polynomial fitting and area division technology, which is applied in the field of interharmonic detection based on polynomial fitting and non-interference area division, can solve the problems of excessive separation, insufficient separation, and influence on the accuracy of detection results. The effect of high detection accuracy, high detection accuracy, and strong resistance to spectrum leakage

Active Publication Date: 2020-08-04
CHINA THREE GORGES UNIV
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Whether the amount of separation is insufficient or the amount of separation is too much, it will affect the accuracy of the detection results
At the same time, due to the extremely high accuracy requirements of harmonic detection results, such methods may not be able to fully meet their accuracy requirements

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Interharmonic detection method based on polynomial fitting and non-interference area division
  • Interharmonic detection method based on polynomial fitting and non-interference area division
  • Interharmonic detection method based on polynomial fitting and non-interference area division

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

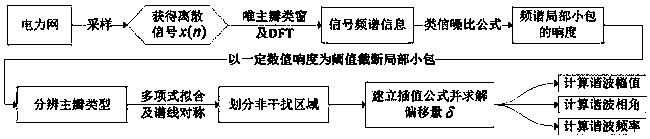
[0052] The interharmonic detection method based on polynomial fitting and non-interference area division includes the following steps:

[0053] Step 1; Acquire a discrete signal containing interharmonics.

[0054] The signal is defined here as shown in formula (1):

[0055]

[0056] in:

[0057] N is the total length of the signal, and each sampling point n=0, 1, 2, . . . , N-1.

[0058] f z 、A z , are the frequency, amplitude, and phase angle of the zth harmonic, and Z is the total harmonic order;

[0059] T s is the time interval between two adjacent sampling points, if the sampling frequency is F s , then T s =1 / F s .

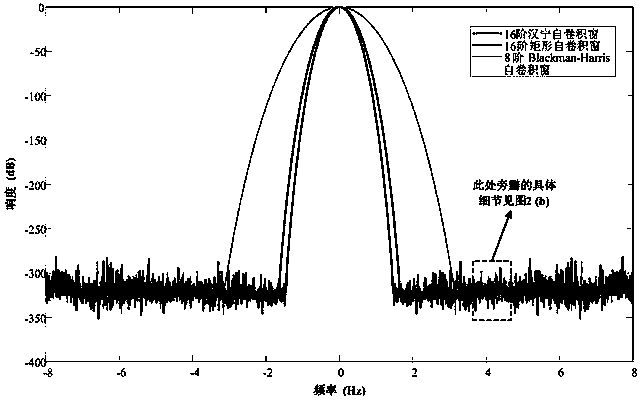
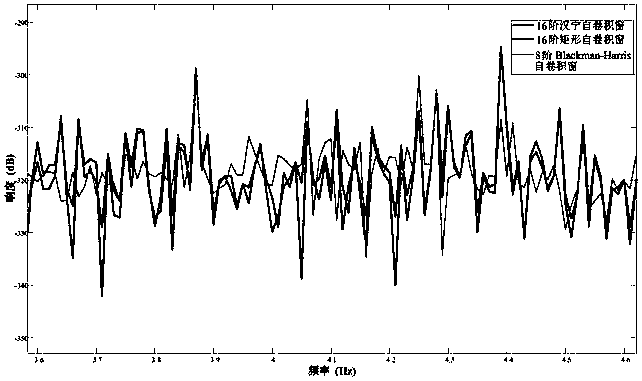
[0060]Step 2: Construct a main lobe-only window function consistent with the discrete signal.

[0061] Here, the 8th-order Blackman-Harris self-convolution window is taken as an example, and its expression is:

[0062] w(n)=[(b*b)*(b*b)]*[(b*b)*(b*b)] (2)

[0063] Wherein, the symbol b refers to a single Blackman-Harris window with a length ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a polynomial fitting and non-interference area division-based interharmonic detection method. The method comprises the steps that an electric power signal is converted into asecondary side dispersion signal through a power transformer; frequency spectrum information of the signal is obtained by means of a specific window function and discrete Fourier transform; sensitivity, relative to a peak value, of a spectral line near a spectrum packet is worked out by adopting a similar signal-to-noise ratio formula; the sensitivity of a certain numerical value serves as a threshold value to cut a packet, the truncation length serves as the basis to distinguish the main lobe type; then the symmetric axis of a spectral line at one side is built through polynomial fitting, thespectral line is symmetrized to the other side, and a non-interference area is marked out; finally, an interpolation formula is built according to the spectral line in the non-interference area, andthe offset is solved. By taking the offset as the basis, parameters such as the amplitude, the frequency and the phase angle of a harmonic wave can be worked out. Accordingly, whether or not main lobejamming occurs in the frequency domain of the signal can be distinguished, and on the condition that main lobe jamming occurs, the area which is not disturbed or disturbed less can be effectively marked out.

Description

technical field [0001] The invention belongs to the technical field of harmonic signal detection in power systems, and in particular relates to an interharmonic detection method based on polynomial fitting and non-interference area division. Background technique [0002] With the improvement of users' requirements on power quality, how to accurately detect and filter harmonics is particularly important. At present, active filtering technology can better control the harmonic problem. An important part of this technology is to use discrete Fourier transform (DFT) to process the signal, so as to analyze the information related to the harmonic. [0003] In recent years, various advanced window functions and various complex interpolation formulas have been introduced into the circuit of Fourier transform, and the detection accuracy of conventional harmonics has been able to reach a relatively ideal level. Errors caused by "spectrum leakage" and "fence effect" can be effectively...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01R23/16
CPCG01R23/16
Inventor 徐艳春杜于飞李振兴李振华
Owner CHINA THREE GORGES UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com