High speed rotating shafting dynamic radial loading stiffness test method and device
A high-speed rotating shaft and testing device technology, which is applied in the direction of measuring devices, testing of mechanical components, testing of machine/structural components, etc., can solve the problems of limited loading force, limited by vibration, difficult to accurately calibrate, etc., and achieve stable linear loading , non-linear, easy-to-load effects
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
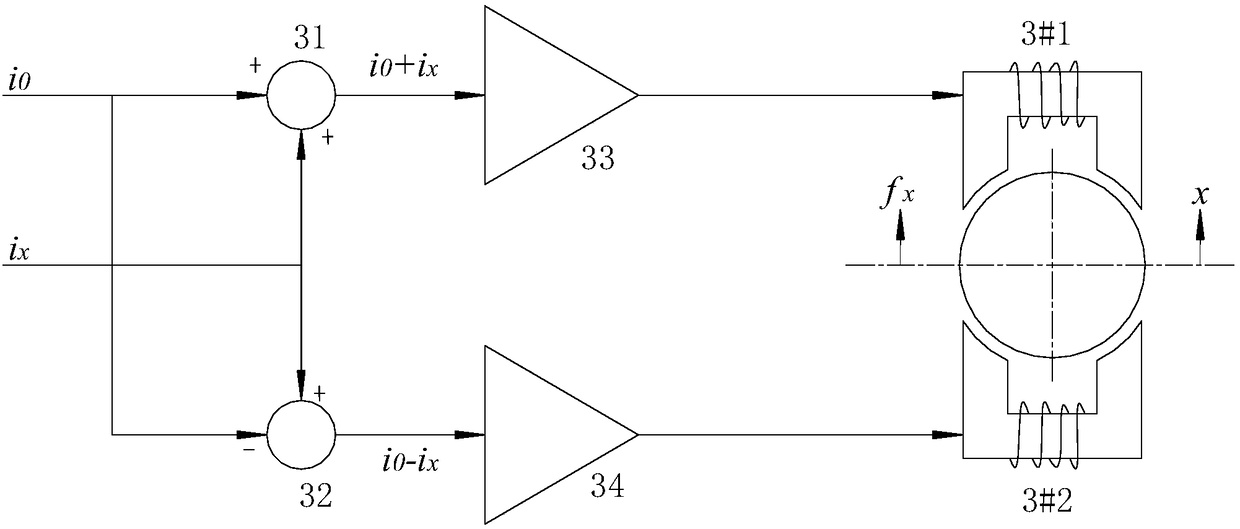
[0043] The implementation steps of the dynamic radial loading stiffness testing method of the high-speed rotating shaft system in this embodiment include:
[0044] 1) Install the rotor on the rotating shaft of the high-speed rotating shaft system under test in advance, install two electromagnetic windings for applying radial magnetic attraction force to the rotating shaft through the rotor on the flange, and at least one for detecting the radial displacement of the rotating shaft Displacement sensor, the two electromagnetic windings are arranged symmetrically with respect to the rotor; the drive current output to one electromagnetic winding during the test is i 0 + i x , the driving current output to another electromagnetic winding is i 0 -i x , where i 0 is the reference current, i x In order to control the current, record the change of the driving current over time and the radial displacement output by the displacement sensor, and jump to the next step;
[0045] 2) Dete...
Embodiment 2
[0065] This embodiment is basically the same as Embodiment 1, and the main difference is that in step 4), only the Fourier transform result of the radial magnetic attraction applied to the rotating spindle and the Fourier transform result of the radial displacement of the rotating spindle are calculated. The ratio between is output as the second dynamic stiffness obtained from the test. The function expression for calculating the second dynamic stiffness is shown in formula (2):
[0066]
[0067]
[0068]
[0069] In formula (2), K(ω) is the second dynamic stiffness (quantity that varies with frequency), F(ω) is the Fourier transform result of the radial magnetic attraction force f(t) applied to the rotating spindle, and X( ω) is the Fourier transform result of the radial displacement x(t) of the rotating spindle, f(t) is the radial magnetic attraction force applied to the rotating spindle, x(t) is the radial displacement of the rotating spindle, and t is time .
Embodiment 3
[0071] This embodiment is basically the same as Embodiment 1, and the main difference is that in step 1), not only the ratio between the radial magnetic force applied to the rotating spindle and the radial displacement of the rotating spindle is calculated as the first dynamic stiffness output obtained from the test At the same time, the ratio between the Fourier transform result of the radial magnetic attraction force applied to the rotating spindle and the Fourier transform result of the radial displacement of the rotating spindle is calculated as the second dynamic stiffness output obtained from the test. The second dynamic stiffness For the calculation details, please refer to Example 2.
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - Generate Ideas
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com