Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method and circuit for realizing fast Fourier transform/fast Fourier inverse transform

A technology of inverse Fourier transform and Fourier transform, which is applied in the field of data transformation and can solve the problems of complete loss of data and reduction of calculation accuracy.

Active Publication Date: 2018-12-07
MONTAGE SEMICON SHANGHAI CO LTD +1
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the above algorithm has problems in accuracy, especially when the data distribution is uneven, the operation accuracy will be greatly reduced
This is because, when the dynamic range between the data is greater than the data bit width, in order to ensure that the maximum value can be represented, all data may be scaled and rounded, resulting in a complete loss of smaller data

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method and circuit for realizing fast Fourier transform/fast Fourier inverse transform
  • Method and circuit for realizing fast Fourier transform/fast Fourier inverse transform
  • Method and circuit for realizing fast Fourier transform/fast Fourier inverse transform

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

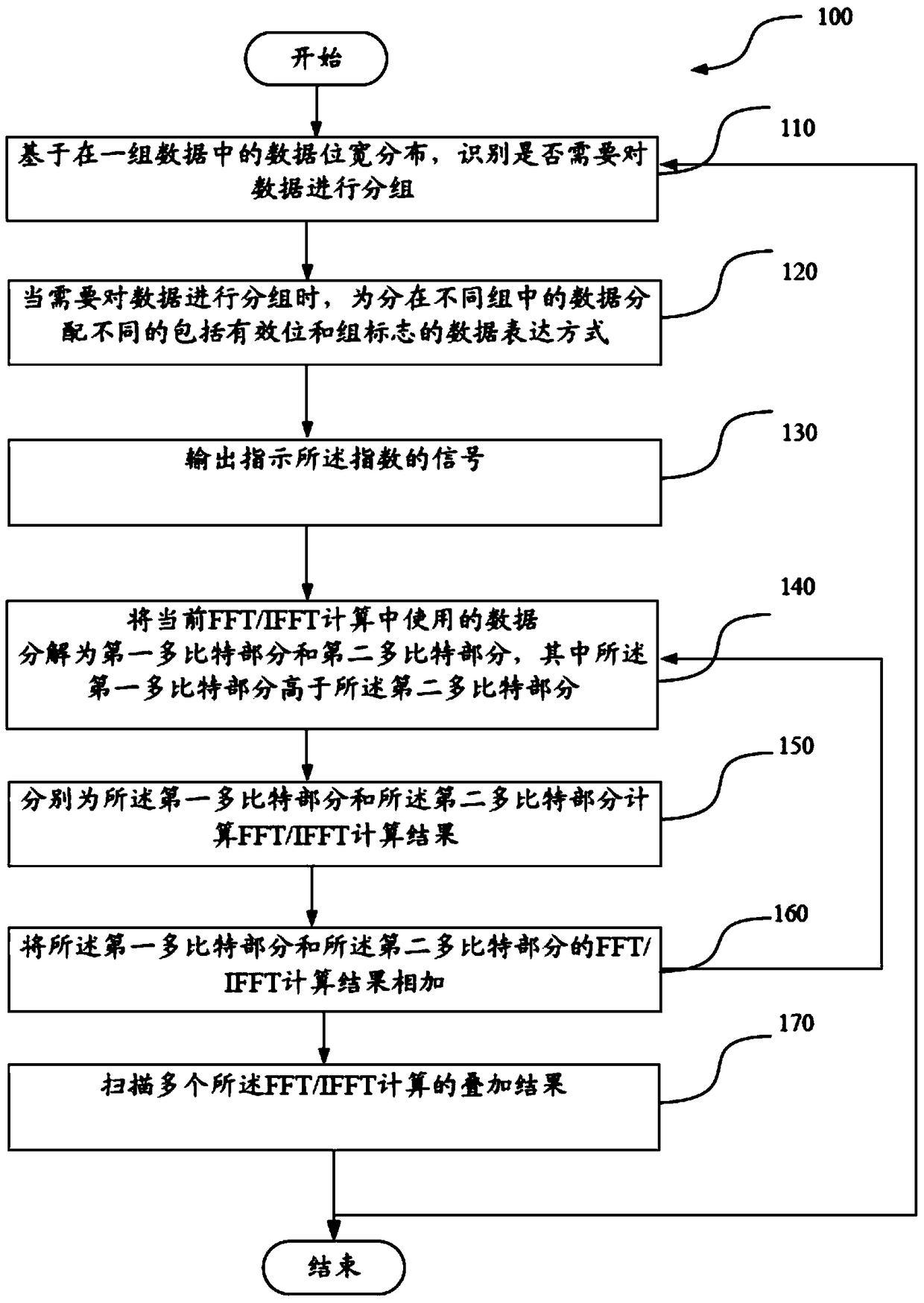
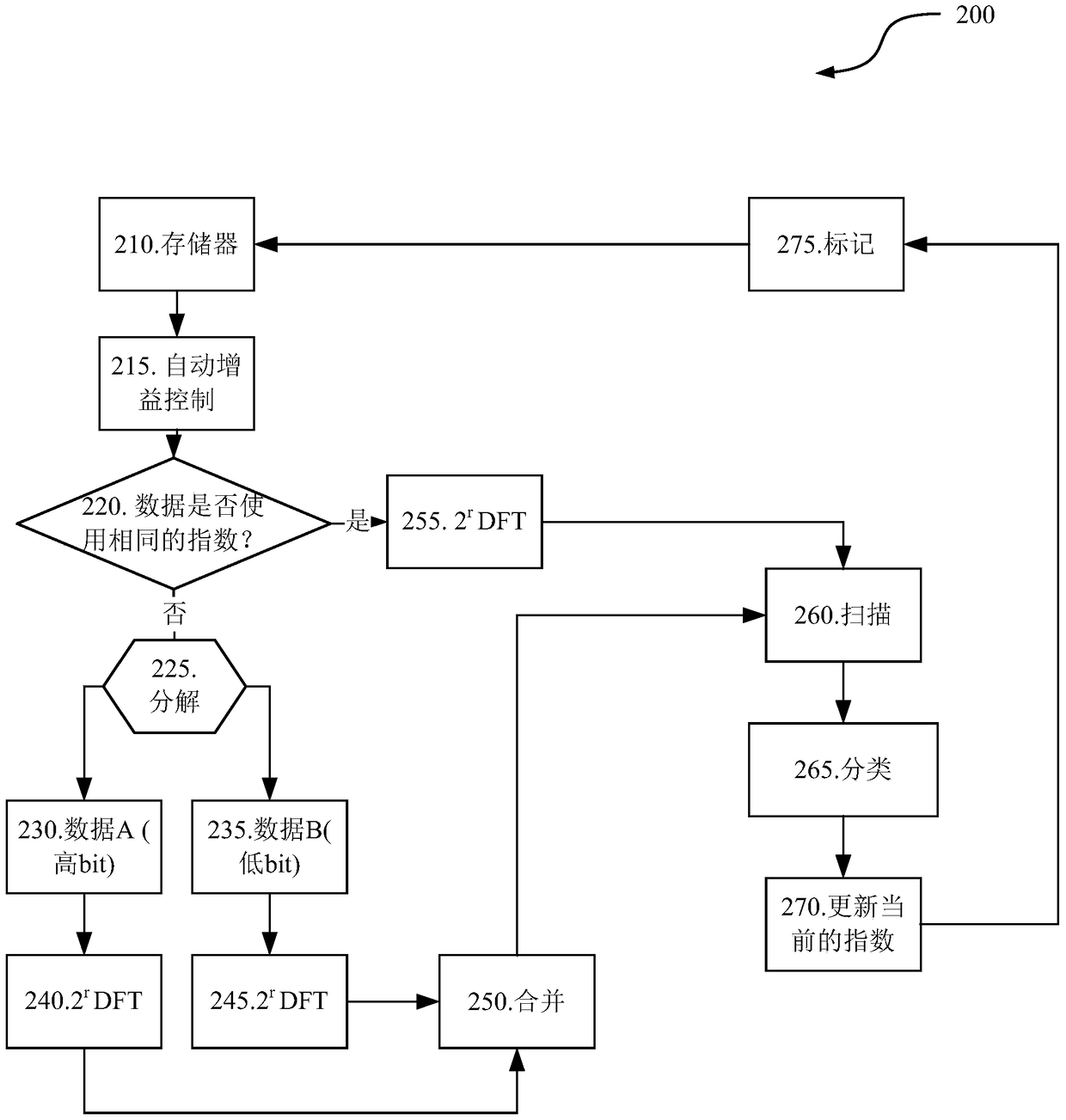
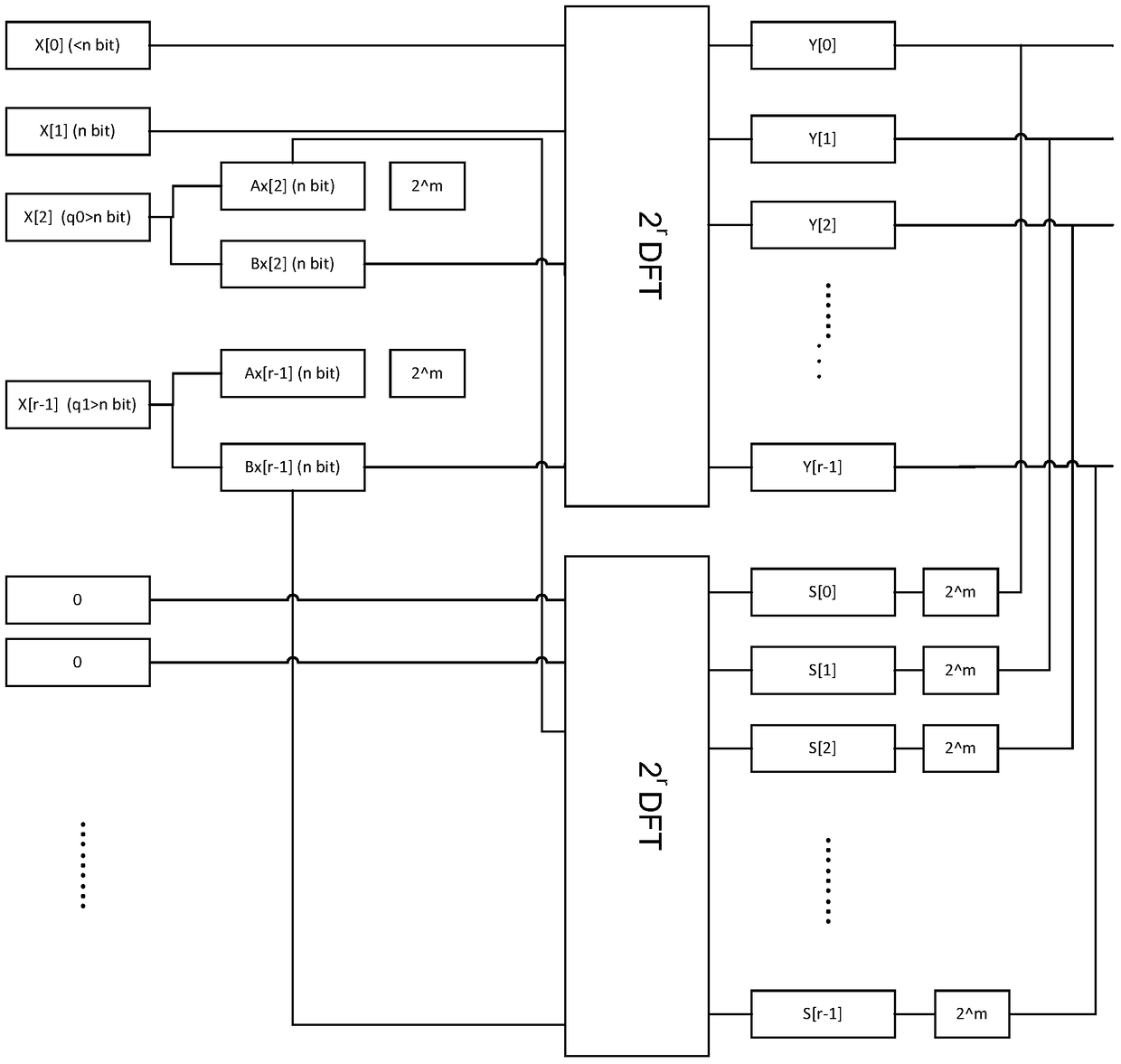
[0022] For example, the bit width Ns of the FFT / IFFT calculator is 12 bits. The data size (that is, the bit width) used by the first-level calculation result is 15 bits (Ns+3 bits), and the number of data with a bit width of 15 bits is 2, that is, M3=2, 14 bits (Ns+2 bits) , corresponding to M2=3, 13 bits (Ns+1 bit), corresponding to M1=23, and less than or equal to (≤) Ns bits, including 10 bits, 8 bits, 6 bits, and 3 bits, corresponding to M0=100. Let the threshold be 10. According to the data distribution, the number of data with a bit width greater than 13 bits is 5, and the number of data with a bit width greater than or equal to 13 bits is 28, and the threshold is 10. Therefore, the number of data with a bit width greater than 13 bits is less than the threshold 10, and the number of data with a bit width greater than or equal to 13 bits is greater than the threshold 10. Then according to Table 1, x=1, the corresponding gain is 2 -1 .

Embodiment 2

[0024] Threshold is still 10. In another embodiment, for example, the bit width Ns of the FFT / IFFT calculator is still 12 bits. The data size (that is, the bit width) used in the first-level calculation is 15 bits (Ns+3 bits), and the number of data with a bit width of 15 bits is 18, that is, M3=18, 14 bits (Ns+2 bits) , corresponding to M2=3, 13 bits (Ns+1 bit), corresponding to M1=23, and ≤Ns bits, including 10 bits, 8 bits, 6 bits, and 3 bits, corresponding to M0=84. Because the number of data with any bit width is greater than the threshold 10, that is, the distribution of data is uniform, therefore, there is no need to group the data. Therefore, the gain is consistent with that obtained by the traditional method, which is 2 -3 .

[0025] In summary, it can be noticed that when the data is uniform, there will be quite a lot of data at the maximum bit width, generally more than the set threshold, and the AGC gain 1 of the control group will be the same as the AGC gain 2 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method for implementing fast Fourier transform / inverse fast Fourier transform, including identifying whether data needs to be grouped based on the data bit width distribution in a set of data, and when the data needs to be grouped, it is divided into assigning different data representations including significant bits and group flags to data in different groups, wherein data in one group has the same index and data in different groups has different indices; and outputting a signal indicating the index; For each of the plurality of short-sequence FFT / IFFT calculations, decomposing the data used in the current short-sequence FFT / IFFT calculation into at least a first multi-bit part and a second multi-bit part; respectively the first multi-bit part and the second multi-bit part Computing the FFT / IFFT calculation results of the two multi-bit parts; adding the FFT / IFFT calculation results of the first multi-bit part and the second multi-bit part; scanning the superposition results of multiple short sequence FFT / IFFT calculations in one stage.

Description

technical field [0001] The invention relates to data transformation, in particular to a method and circuit for realizing fast Fourier transform / fast Fourier inverse transform. Background technique [0002] The operation of FFT / IFFT satisfies Pasval's theorem, that is, the energy of the output data is N times the energy of the input data. This shows that if a lossless operation requires a large storage space, the operator also needs a large bit width. In order to save resources, the maximum value of the overall data is generally scanned after each iteration is completed, and the overall data is multiplied or divided by a constant power of 2 to determine the constant according to the maximum value, and the effective data with less bit width is saved. Compensate the same factor on the iteration result. This common method is called automatic gain. However, the above algorithms have problems in accuracy, especially when the data distribution is uneven, the operation accuracy w...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/14
CPCG06F17/142H04L27/263H04L27/2651H04L27/2636
Inventor 宋鹤鸣
Owner MONTAGE SEMICON SHANGHAI CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com