Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Tunable semiconductor laser

A technology of lasers and semiconductors, applied in semiconductor lasers, lasers, laser components, etc., can solve problems such as inconsistent output optical power, achieve flat reflection peak response, ensure stability, and simple design of grating structure parameters

Inactive Publication Date: 2013-04-24
HUAZHONG UNIV OF SCI & TECH
View PDF3 Cites 13 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0010] The technical problem to be solved by the present invention is to provide a tunable semiconductor laser, which can improve the inconsistency of the output optical power of each wavelength channel in the prior art when the laser is tuned, and can realize a wide wavelength tuning range. Good model characteristics, high side mode suppression ratio and high output power

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Tunable semiconductor laser
  • Tunable semiconductor laser
  • Tunable semiconductor laser

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

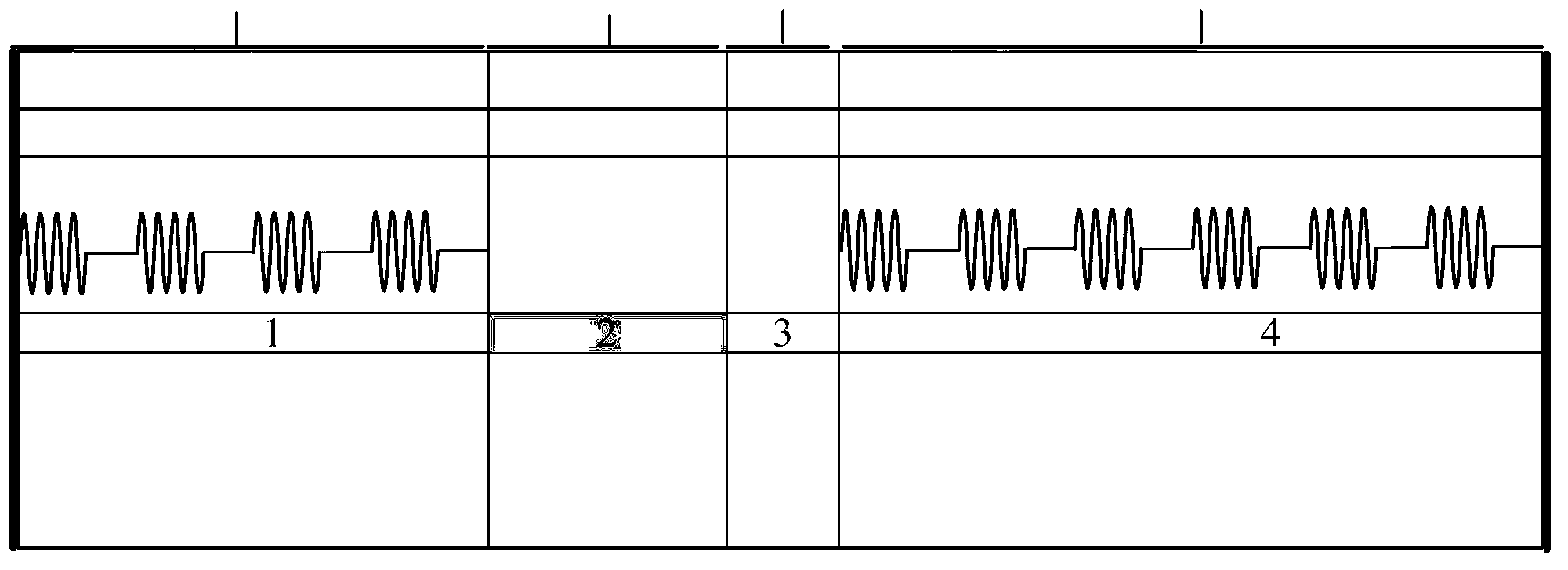
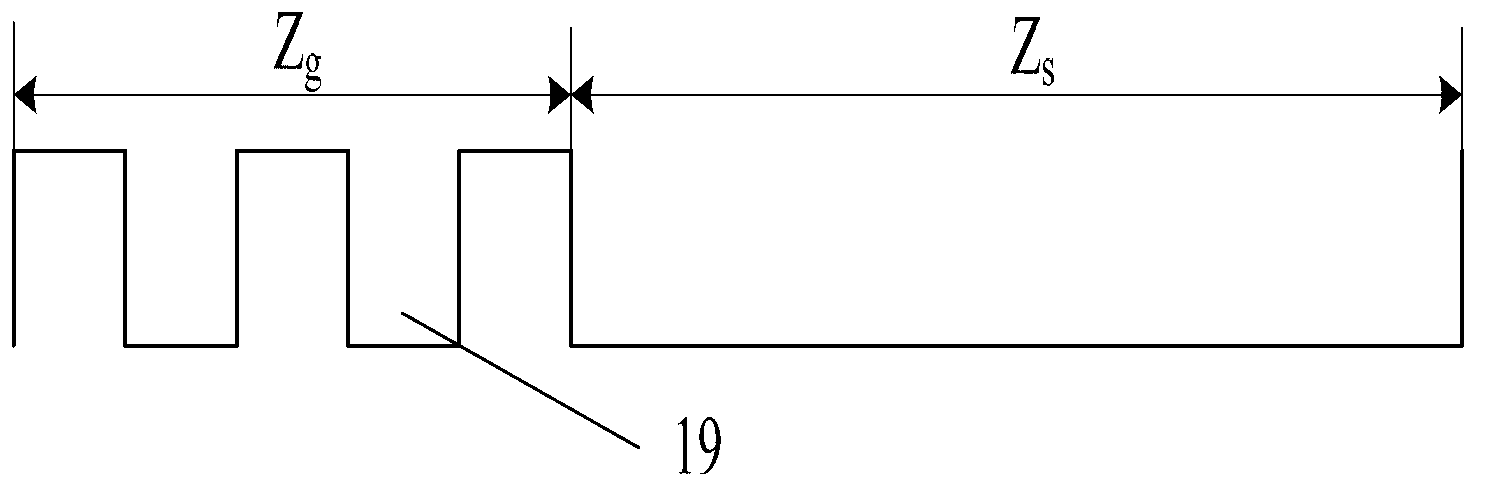
[0075]In the first embodiment, the number of sub-segments of the front and rear multi-phase-shift digital cascaded Bragg gratings 9 and 10 is 3, and the multiplication factor of the number of channels is 2, that is, m=2, M=3, n=2, N=3. Figure 6 It is a structural schematic diagram of the front and rear multi-phase shift digital cascaded Bragg gratings in the first embodiment. For the front and rear multi-phase shift digital cascade Bragg gratings 9, 10, according to the formula φ kf =k×2π / m (pre-multi-phase shift digital cascaded Bragg grating 9) and φ kr =k×2π / n (post multi-phase shift digital cascaded Bragg grating 10), then the grating initial phase difference φ between the k+1 sampling period and the k sampling period kf with φ kr Both are kπ. The parameters used in the front and rear multi-phase shift digital cascaded Bragg gratings 9 and 10 are shown in Table 1 below. The effective refractive index n eff Choose 3.21.

[0076] Table 1: Structural parameter table of...

Embodiment 2

[0081] In the second embodiment, the number of sub-segments of the front and rear multi-phase-shift digital cascaded Bragg gratings 9 and 10 is 3, and the multiplication factor of the number of channels is 3, that is, m=3, M=3, n=3, N=3. Figure 11 It is a structural schematic diagram of the front and rear multi-phase shift digital cascaded Bragg gratings 9 and 10 in the second embodiment. For the front and rear multi-phase shift digital cascade Bragg gratings 9, 10, according to the formula φ kf =k×2π / m (pre-multi-phase shift digital cascaded Bragg grating 9) and φ kr =k×2π / n (post multi-phase shift digital cascaded Bragg grating 10), then the grating initial phase difference φ between the k+1 sampling period and the k sampling period kf with φ kr Both are k×2π / 3. The parameters used for the front and rear multi-phase shift digital cascaded Bragg gratings 9 and 10 are shown in Table 2 below. The effective refractive index n eff Choose 3.21.

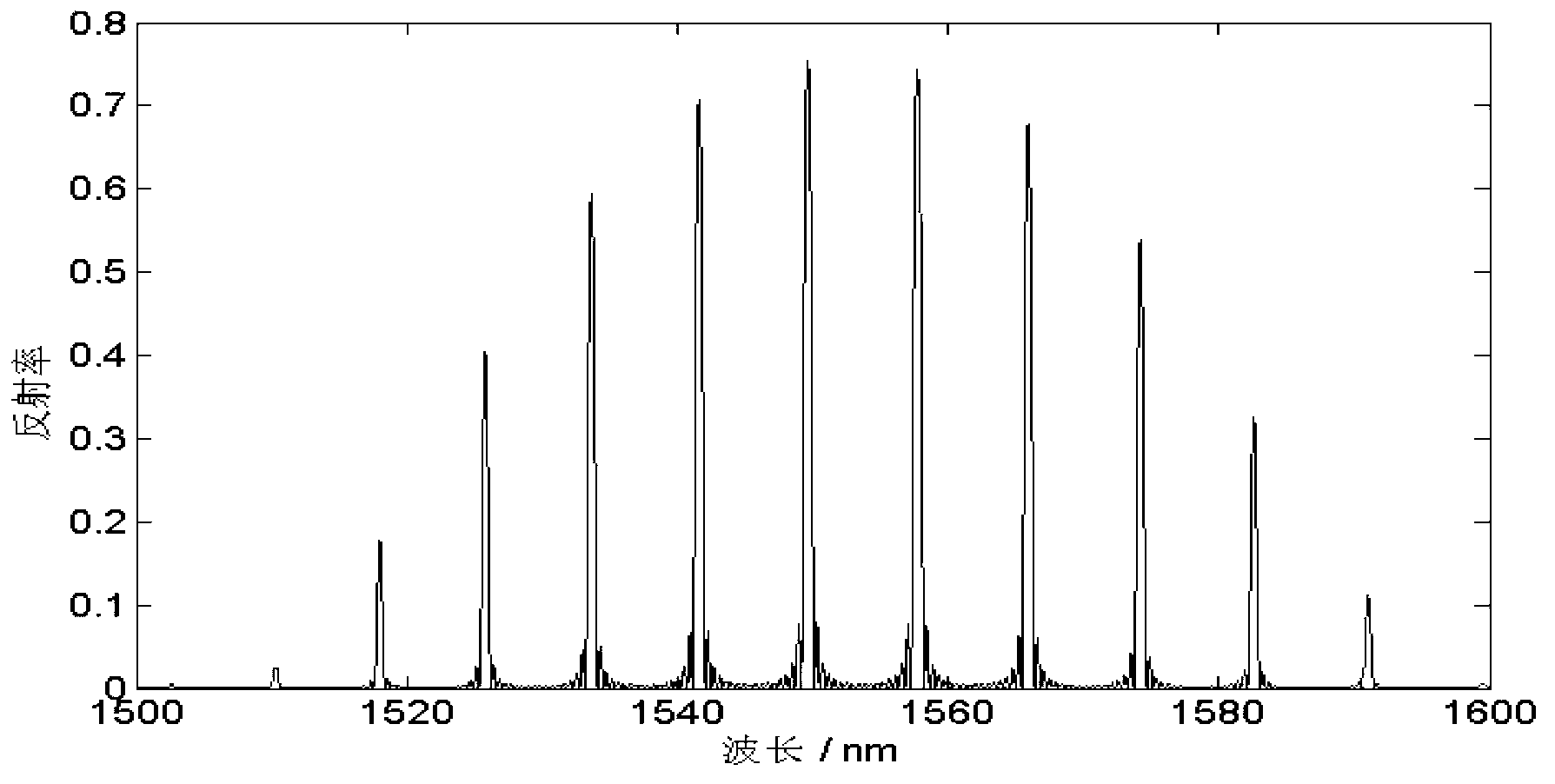
[0082] Figure 12 and Fi...

Embodiment 3

[0087] In the third embodiment, the number of sub-segments of the front and rear multi-phase-shift digital cascaded Bragg gratings 9 and 10 is 4, and the multiplication factor of the number of channels is 2, that is, m=2, M=4, n=2, N=4. Figure 14 It is a schematic diagram of the structure of the front and rear multi-phase shift digital cascaded Bragg gratings in the third embodiment. For the front and rear multi-phase shift digital cascade Bragg gratings 9, 10, according to the formula φ kf =k×2π / m (pre-multi-phase shift digital cascaded Bragg grating 9) and φ kr =k×2π / n (post multi-phase shift digital cascaded Bragg grating 10), then the grating initial phase difference φ between the k+1 sampling period and the k sampling period kf with φ kr Both are kπ. The parameters used in the front and rear multi-phase shift digital cascaded Bragg gratings 9 and 10 are shown in Table 3 below. The effective refractive index n eff Choose 3.21.

[0088] Table 3: Structural parameter ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a tunable semiconductor laser. A front multi-phase shift digital cascade Bragg grating and a rear multi-phase shift digital cascade Bragg grating are respectively manufactured in an upper limit layer of a front grating area and an upper limit layer of a rear grating area and are respectively manufactured through adding phase shift in an adjacent sampling period of a digital cascade Bragg grating. Peak homogeneity of a reflectance spectrum of the multi-phase shift digital cascade Bragg grating is good. Due to the fact that the multi-phase shift digital cascade Bragg grating is in cascade connection with the reflectance spectrum, the number of reflecting channel in the bandwidth of the reflectance spectrum is increased by several times. Meanwhile, multi-phase shift technology is adopted so that the number of reflecting channel of the reflectance spectrum of the multi-phase shift digital cascade Bragg grating is increased by several times again so that a tuning range that the laser can reach is wider.

Description

technical field [0001] The invention relates to a tunable semiconductor laser, which belongs to the field of optical fiber communication and laser technology. The laser is a Bragg reflective laser based on multi-phase-shift digital cascaded Bragg gratings. Background technique [0002] With the development of ultra-high-speed and large-capacity optical fiber communication technology, tunable semiconductor lasers play a very important role in Dense Wavelength Division Multiplexing (DWDM) systems. A tunable semiconductor laser can replace multiple fixed-wavelength lasers, thus reducing the manufacturing cost of the laser, simplifying the module packaging process, and reducing the cost of backup and inventory management; in optical network systems, the wavelength of the tunable laser can be adjusted The performance can allow the dynamic configuration of the wavelength on the optical route, so it can reduce the delay and improve the transmission capacity of the optical network i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H01S5/125
Inventor 赵家霖余永林
Owner HUAZHONG UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com