Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Methods, computer-accessible medium and systems to model disease progression using biomedical data from multiple patients

a disease progression and patient technology, applied in the field of cancer progression models, can solve the problems of not being able to achieve every order, the causal and temporal relationship among the genetic events driving cancer progression remains largely unknown, and the impact of large-scale effects

Inactive Publication Date: 2016-10-13
NEW YORK UNIV +1
View PDF0 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

The patent describes a system, method, and computer-accessible medium for creating a model that can show how a disease progresses in a patient. The model is based on data collected from the patient's genes, proteins, and other biomarkers. This model can help doctors better understand and treat the disease. The system can also receive data from subsequent patients and use it to classify the disease and suggest treatments.

Problems solved by technology

Different progression sequences can be used, although some can be more common than others, and not every order can be viable.
However, unfortunately, the causal and temporal relations among the genetic events driving cancer progression remain largely elusive.
Extracting this dynamic information from the available static, or cross-sectional data can be a challenge, and the combination of mathematical, statistical and computational techniques can be needed to decipher the complex dynamics.
The results of the research addressing these issues will have important repercussions for disease diagnosis and prognosis, and therapy.
However, in these cases, other constraints on the joint occurrence of events can be imposed.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Methods, computer-accessible medium and systems to model disease progression using biomedical data from multiple patients
  • Methods, computer-accessible medium and systems to model disease progression using biomedical data from multiple patients
  • Methods, computer-accessible medium and systems to model disease progression using biomedical data from multiple patients

Examples

Experimental program
Comparison scheme
Effect test

case iii

[0351]

[0352]The derivation below shows, just like in the DMPN, that θ+> for all true parents sets in the XMPN. The reasoning behind this can be similar to that above, except for the summation can be over the rows in which exactly one parent takes value 1 and the rest take value 0. To denote this, the standard notation Pai(X) can be used to mean the ith parent of X and Pa−i(X) to mean all parents except for the ith parent of X.

[0353]Lemma 3 (Consistency of Polaris):

[0354]Polaris can be a statistically consistent score.

[0355]Exemplary Proof:

[0356]Let M be the number of samples generated by the graph G*=(V, E*). Let G=(V, E) be the graph learned by maximizing the Polaris score, and GBIC be the graph learned by maximizing the BIC score, both for a sufficiently large M. The exemplary Polaris score can consist of three terms: (i) the log-likelihood (LL) term, (ii) the regularization term from BIC and (iii) the monotonicity term. Each of these terms can grow at different rates. The LL term...

case vi

[0368]

[0369]Xi has 2 or more parents. Because G* has no transitive edges, there cannot be any edge between any two parents of Xi. Thus, the parents of Xi can be unwed and form a v-structure with Xi. Because Polaris can be consistent, this v-structure can be learned correctly.

[0370]Exemplary Corollary 1 (Convergence Conditions for Polaris with Filtering):

[0371]For a sufficiently large sample size, M, under the assumptions of no transitive edges and faithful temporal priority relations, filtering with the α-filter and then optimizing Polaris convergences to the exact structure for MPNs. Proof:

[0372]In Lemma 1, it was shown that α-filtering removes no true parent sets. In Theorem 6, it was shown that given a hypothesis space that includes the true parent sets, optimizing Polaris returns the true graph. Because the α-filter does not remove the true parent sets from the hypothesis space, optimizing Polaris will still return the correct structure on the filtered hypothesis space.

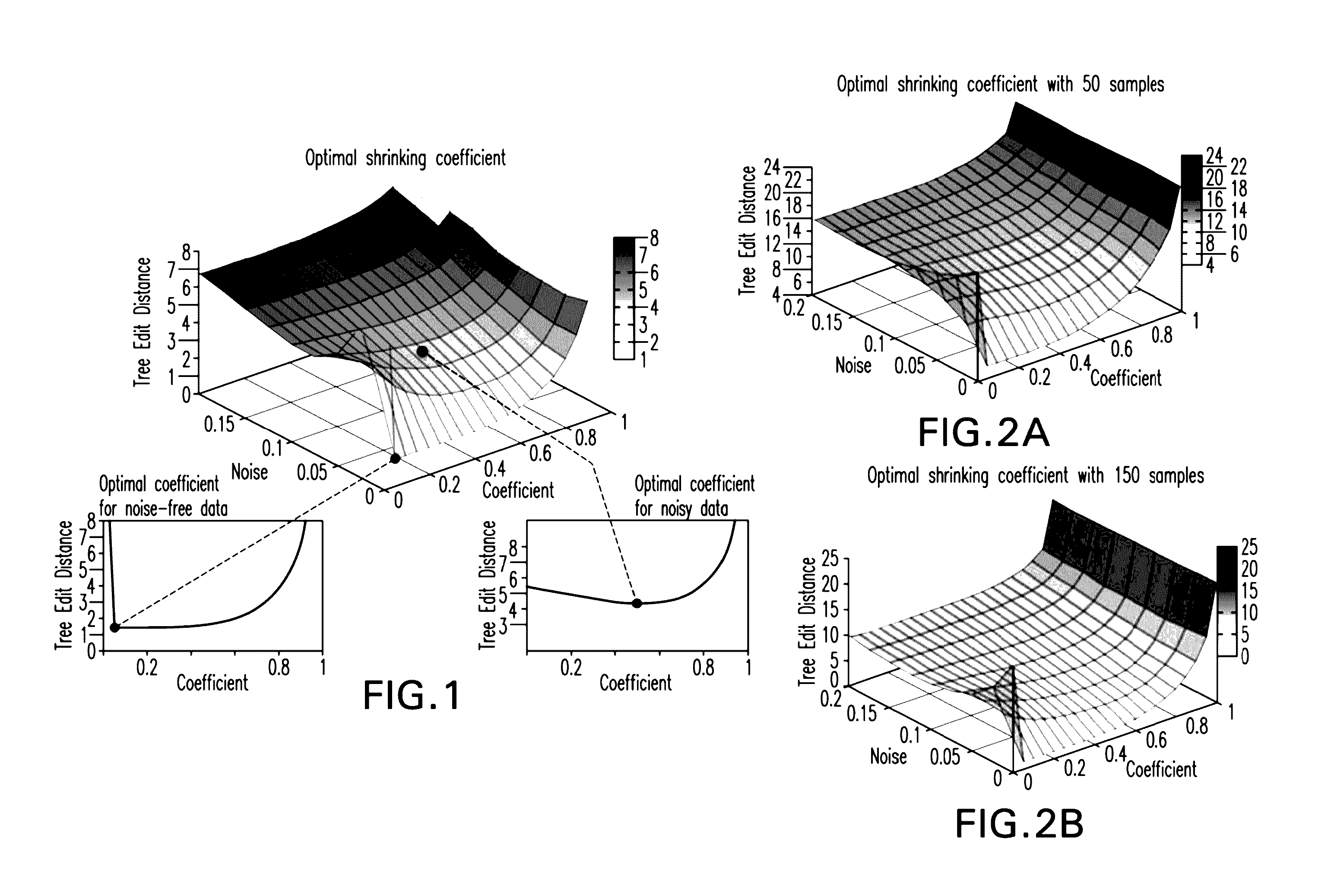
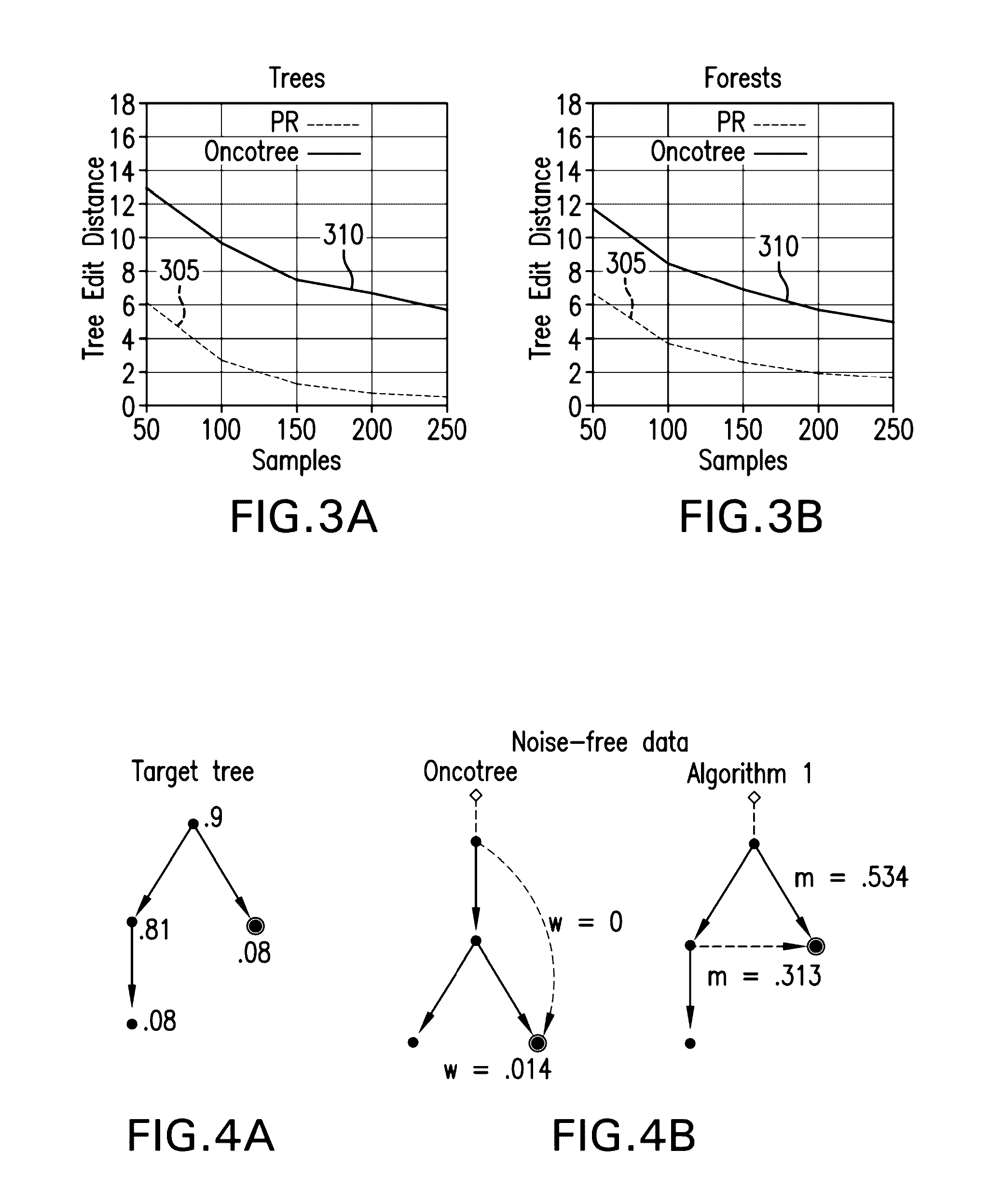
[0373]FIG...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

An exemplary embodiment of system, method and computer-accessible medium can be provided to reconstruct models based on the probabilistic notion of causation, which can differ fundamentally from that can be based on correlation. A general reconstruction setting can be complicated by the presence of noise in the data, owing to the intrinsic variability of biological processes as well as experimental or measurement errors. To gain immunity to noise in the reconstruction performance, it is possible to use a shrinkage estimator. On synthetic data, the exemplary procedure can outperform currently known procedures and, for some real cancer datasets, there are biologically significant differences revealed by the exemplary reconstructed progressions. The exemplary system, method and computer accessible medium can be efficient even with a relatively low number of samples and its performance quickly converges to its asymptote as the number of samples increases.

Description

CROSS-REFERENCE TO RELATED APPLICATIONS[0001]This application relates to and claims priority from U.S. Patent Application No. 61 / 896,566, filed on Oct. 28, 2013, U.S. Patent Application No. 62 / 038,697, filed on Aug. 18, 2014, and U.S. Patent Application No. 62 / 040,802, filed on Aug. 22, 2014, the entire disclosures of which are incorporated herein by reference.FIELD OF THE DISCLOSURE[0002]The present disclosure relates generally to cancer progression models, and more specifically, to exemplary embodiments of an exemplary system, method and computer-accessible medium for a determination of cancer progression models, which can include noise and / or biological noise and / or can use biological data from multiple patients.BACKGROUND INFORMATION[0003]Cancer is a disease of evolution. Its initiation and progression can be caused by dynamic somatic alterations to the genome manifested as point mutations, structural alterations of the genome, DNA methylation and histone medication changes. (Se...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(United States)
IPC IPC(8): G06F19/00G16B5/10G16B5/20
CPCG06F19/3437G16H50/50G16B5/00G16H50/70G16B5/20G16B5/10G06N5/00G06N20/00G06N7/01
Inventor RAMAZZOTTI, DANIELECARAVAGNA, GIULIOOLDE LOOHUIS, LOESGRAUDENZI, ALEXKORSUNCKY, IIYAMAURI, GIANCARLOCH, MARCOMISHRA, BHUBANESWAR
Owner NEW YORK UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com