Model selection for cluster data analysis
a cluster data and model selection technology, applied in the field of learning machines, can solve the problems of increasing difficulty in facilitating human comprehension of the information in this data, unapproachable problems, and accelerating growth in the system and method of generating, collecting and storing vast amounts of data, and achieve the effect of facilitating the clustering task and low noise level
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Benefits of technology
Problems solved by technology
Method used
Image
Examples
example 1
Gaussian Data
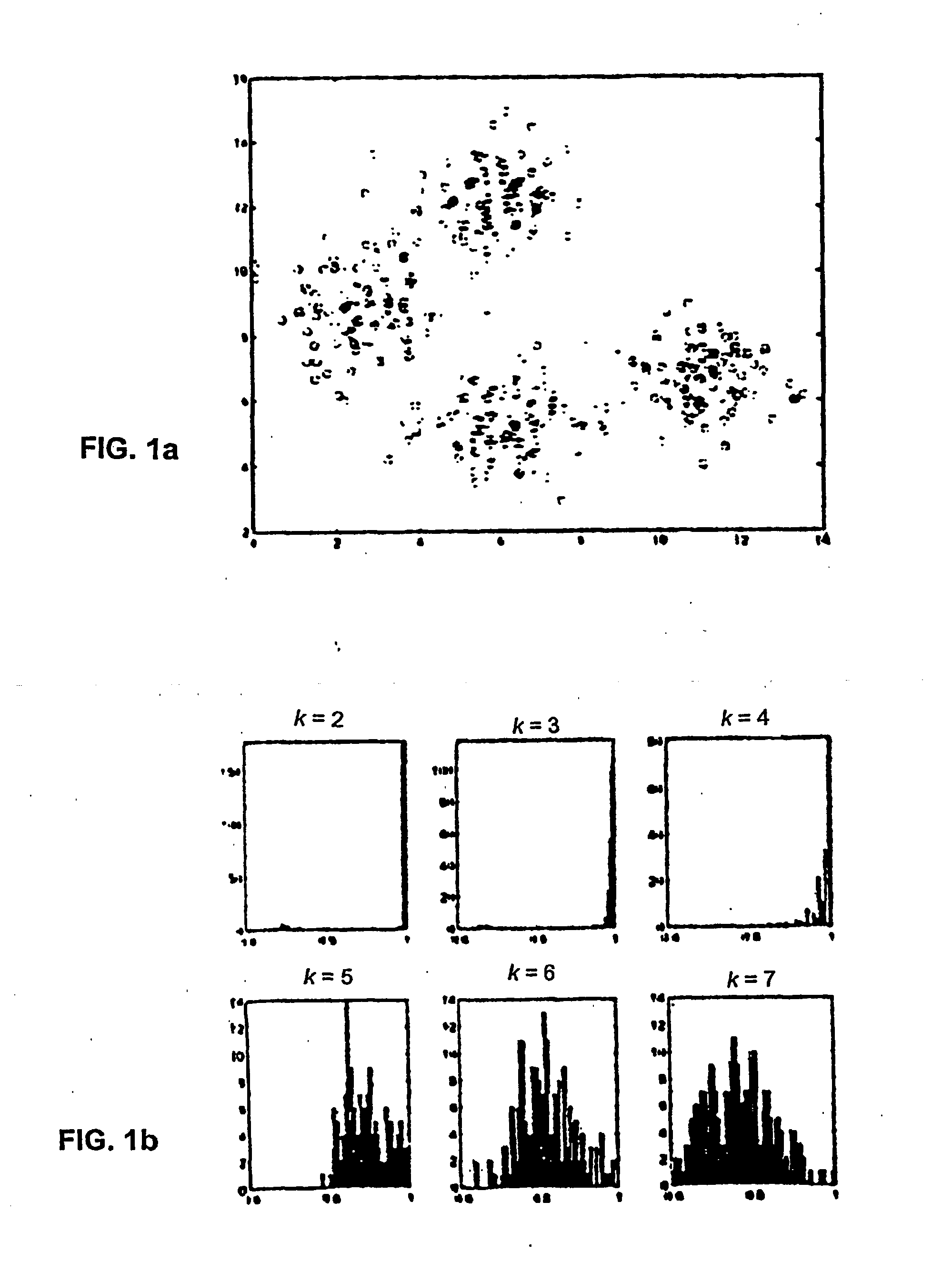
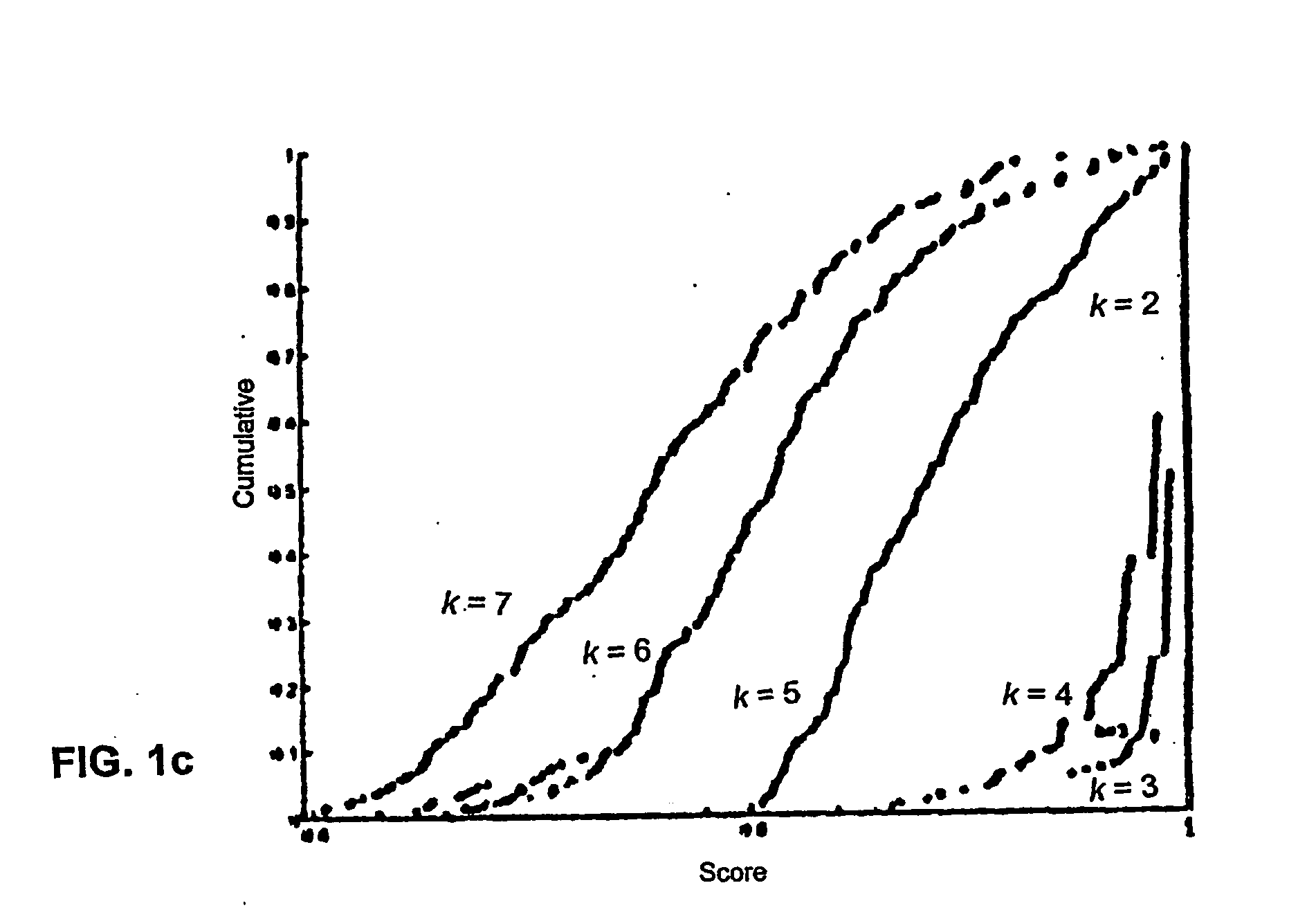
Referring first to FIGS. 1a-1c, FIG. 1a shows a mixture of four Gaussians. The histograms of the score for varying values of k for this data is plotted in FIG. 1b. Histograms are shown for each value of k in the range of 2 to 7. Observations regarding the histograms are that at k=2, there is a peak at 1, since almost all the runs discriminated between the two upper and two lower clusters. At k=3, most runs separated the two lower clusters, and at k=4 most runs found the “correct” clustering as is reflected in the distribution of scores that is still close to 1.0. At k>4 there is no longer essentially one preferred solution. There is, in fact, a wide variety of solutions, evidenced by the widening spectrum of the similarities. FIG. 1c plots the cumulative distributions of the correlation score for each k, where k=2 at the rightmost side of the plot (at peak 1), and k=7 being the leftmost curve.
example 2
DNA Microarray Data
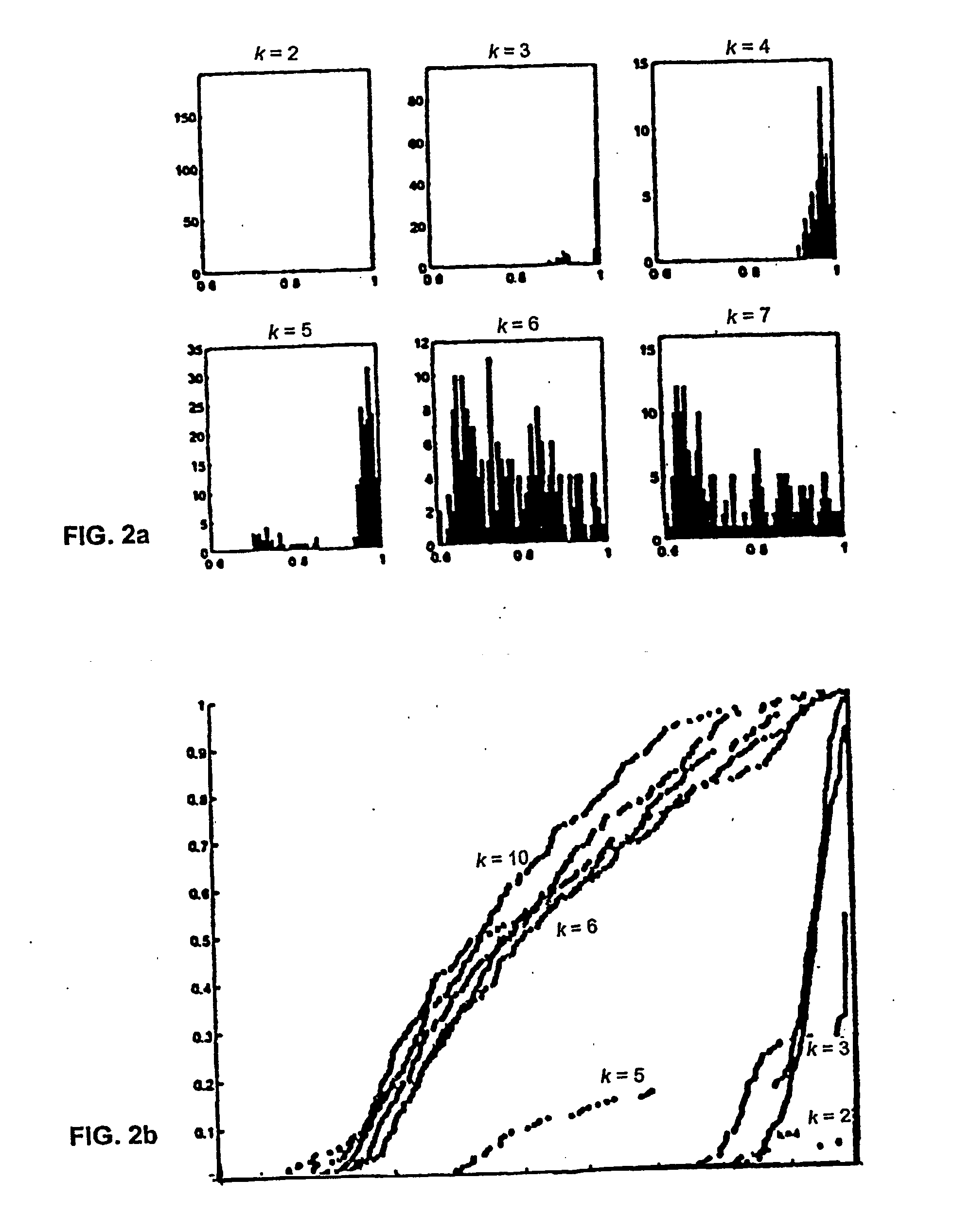
The next dataset considered was the yeast DNA microarray data of M. Eisen et al. (“Genetics cluster analysis and display of genome-wide expression patterns”, Proc. Natl. Acad. Sci. USA, 95: 14863-14868, December 1998. The data is a matrix which represents the mRNA expression levels of n genes across a number of experiments. Some of the genes in the data have known labels according to a functional class. Five functional classes were selected along with genes that belong uniquely to these five functional classes. This yielded a dataset with 208 genes, with 79 features (experiments). Data was normalized by subtracting the mean and dividing by the standard deviation for each column. This was also performed for the rows, and repeated for the columns. At this stage the first three principal components were extracted. The distribution and histogram of scores is give in FIG. 2a fork over the range of 2 to 7. The same behavior is observed as seen in the mixture of four G...
example 3
Uniformly Distributed Data
The results of a test run on data uniformly distributed on the unit cube is shown in FIGS. 3a and 3b. The distributions are quite similar to each other, with no change that can be interpreted as a transformation from a stable set of solutions to unstable solutions.
The preceding examples indicate a simple way for choosing k as the value where there is a transition from a score distribution that is concentrated near 1 to a wider distribution. This can be quantified, e.g., by an increase in the area under the cumulative distribution function or by an increase in
S(K)=P(s>0.90).
The value of 0.9 is arbitrary, but any value close to 1 would work on the set of examples considered here.
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com