Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Discrete cosine transforming method operated for image coding and video coding

A discrete cosine transform, discrete cosine technology, applied in image communication, digital video signal modification, television and other directions, can solve problems such as low complexity, less addition and shift implementation, etc.

Active Publication Date: 2007-01-03
XFUSION DIGITAL TECH CO LTD
View PDF0 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The disadvantage of this structure is that it uses a two-input three-multiplication structure, and in some cases the equivalent two-input four-multiplication structure can be implemented with fewer additions and shifts, with lower complexity and comparable accuracy.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Discrete cosine transforming method operated for image coding and video coding
  • Discrete cosine transforming method operated for image coding and video coding
  • Discrete cosine transforming method operated for image coding and video coding

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

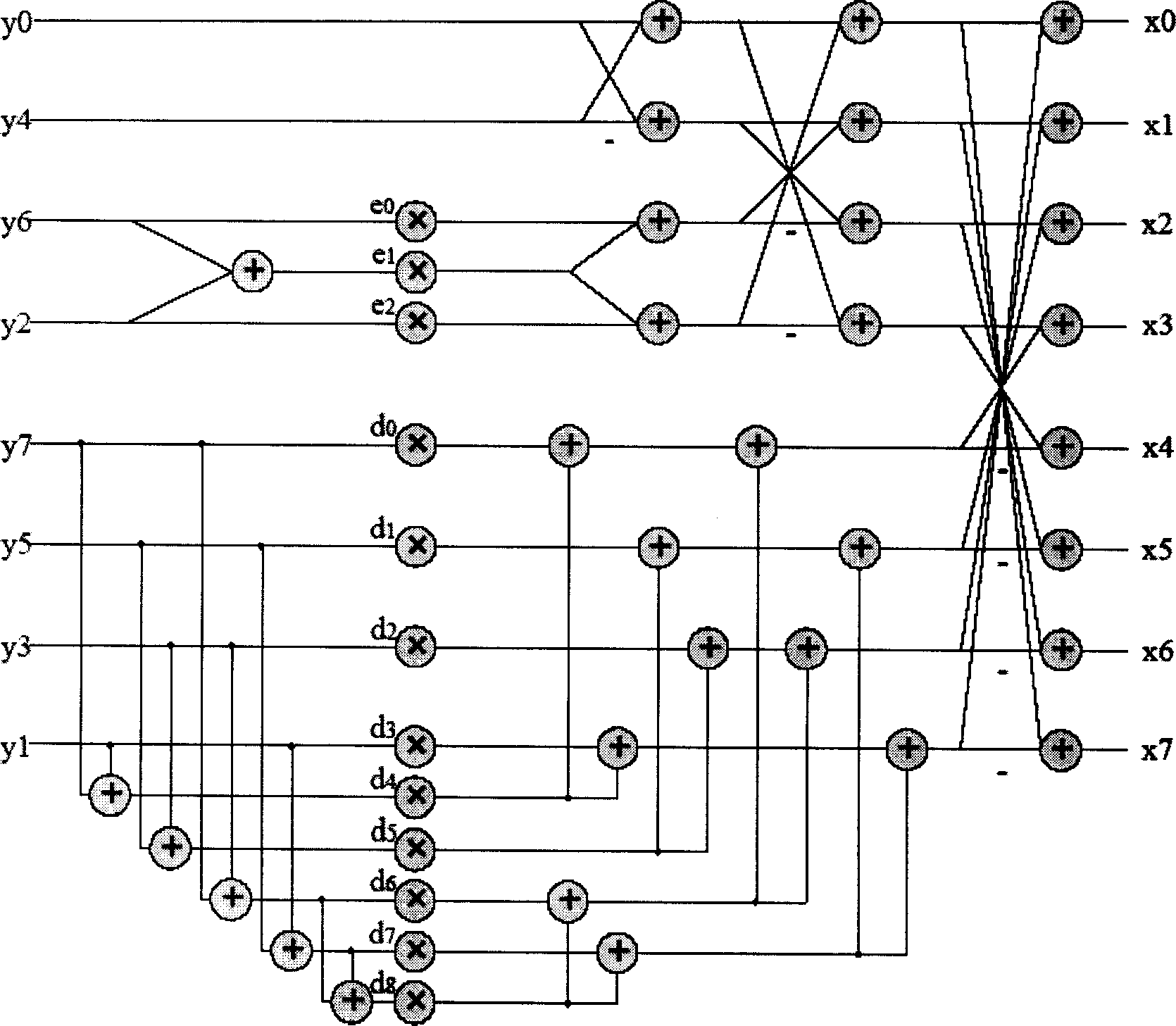
[0052] use image 3 The Inverse Discrete Cosine Transform butterfly structure is shown.

[0053] The inverse discrete cosine transform process is as follows:

[0054] Input the row or column of the 8×8 matrix A into the inverse discrete cosine transform as the input of the butterfly structure of the discrete cosine transform in turn, and output it as the corresponding row or column to obtain the 8×8 intermediate matrix B, and then use the column or row of the matrix B In turn, it is used as the input of the discrete cosine inverse transform butterfly structure, and the output is used as the corresponding column or row to obtain an 8×8 output matrix C.

[0055] image 3 The multiplier parameters in the shown IDCT butterfly structure are as follows: α=cos(3π / 8), β=sin(3π / 8), γ=cos(5π / 16), δ= sin(5π / 16), κ=(cos(π / 16)-cos(5π / 16)), λ=(sin(5π / 16)-sin(π / 16)), μ=(cos (5π / 16)-sin(π / 16)), ν=(cos(π / 16)+sin(5π / 16)), so that the sum of the elements in the matrix C is the two-di...

Embodiment 2

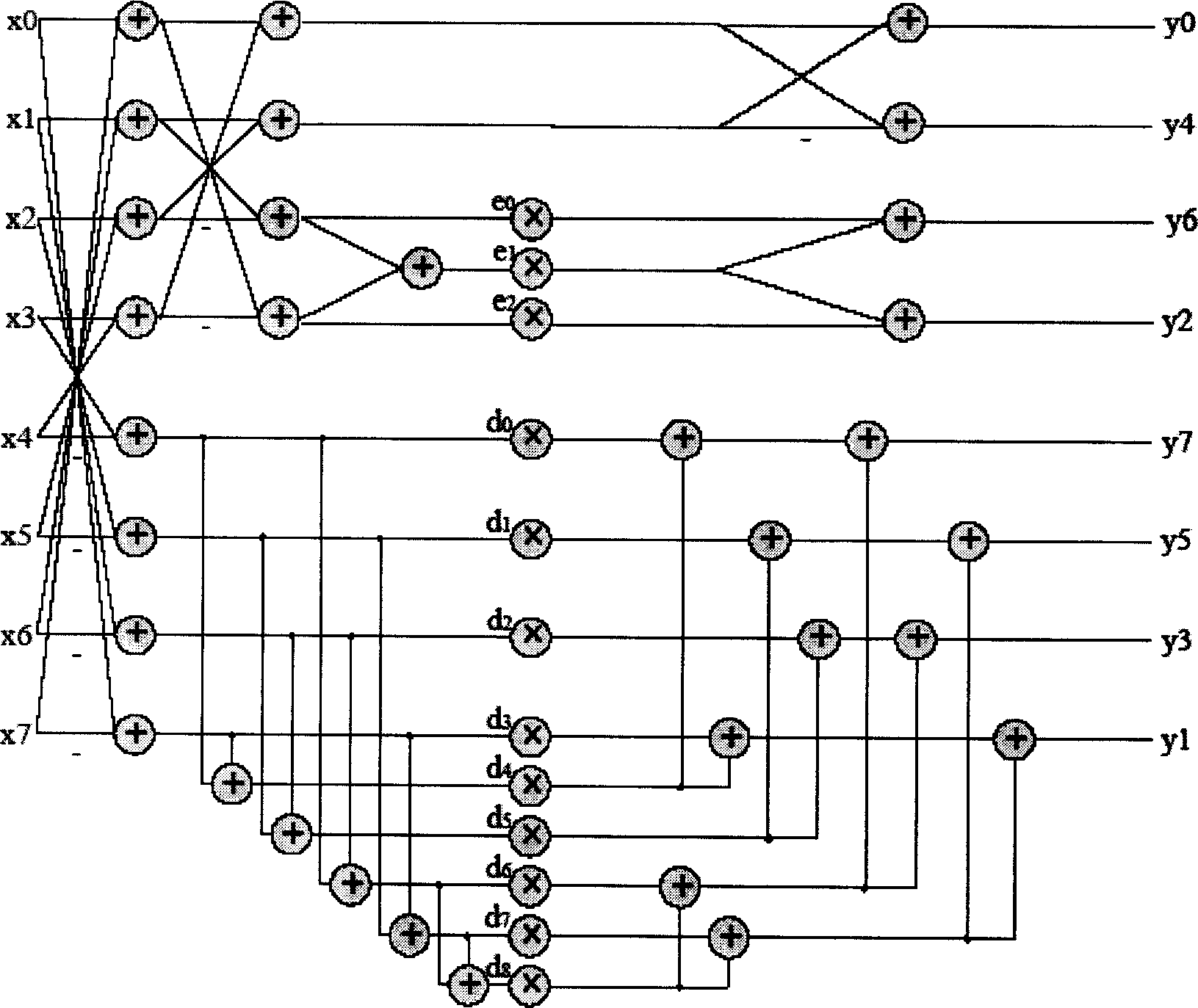
[0057] use Figure 4 The discrete cosine transform butterfly structure is shown.

[0058] The discrete cosine transform process is as follows:

[0059] Input discrete cosine positive transform into the row or column of 8×8 matrix A in turn as the input of discrete cosine positive transform butterfly structure, output as the corresponding row or column to get 8×8 intermediate matrix B, and then the column or row of matrix B In turn, they are used as the input of the discrete cosine positive transform butterfly structure, and the output is used as the corresponding column or row to obtain an 8×8 output matrix C.

[0060] Figure 4 The multiplier parameters in the shown DCT butterfly structure are as follows: α=cos(3π / 8), β=sin(3π / 8), γ=cos(5π / 16), δ= sin(5π / 16), κ=(cos(π / 16)-cos(5π / 16)), λ=(sin(5π / 16)-sin(π / 16)), μ=(cos (5π / 16)-sin(π / 16)), ν=(cos(π / 16)+sin(5π / 16)), so that the sum of the elements in the matrix C is the two-dimensional theoretical discrete cosine sine...

Embodiment 3

[0062] use image 3 The Inverse Discrete Cosine Transform butterfly structure is shown.

[0063] The inverse discrete cosine transform process is as follows:

[0064] Firstly, the input 8×8 matrix A is preprocessed to obtain the 8×8 matrix B. The preprocessing process is as follows: B(i, j)=A(i, j)×S(i, j) 0≤i, j≤7. The matrix S is defined as follows:

[0065] S = a b c d a b c d b d f d b d f ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A discrete cosine transform method used on image coding and video cording includes using two input four multiplication structure to replace two input three multiplication structure to let multiplier with the same input enable to be realized unitedly and simultaneously enabling to pick up the same factor of two input four multiplication structure to be at external of butterfly structure for carrying out pretreatment or / and post treatment so as to decrease bit width and operation frequency required by realizing discrete cosine transform.

Description

technical field [0001] The invention relates to the technical field of electrical digital data processing, in particular to a discrete cosine transform method applied to image coding and video coding. Background technique [0002] Traditional video coding standards such as H.261 and H.263 standards formulated by ITU and MEPG-1, MPEG-2, and MPEG-4 formulated by ISO's MPEG organization are all based on hybrid coding. The so-called hybrid coding framework is a coding framework that comprehensively considers prediction, transformation and entropy coding methods, and has the following main features: [0003] 1) Use prediction to remove redundancy in the time domain; [0004] 2) Use transformation to remove redundancy in the spatial domain; [0005] 3) and remove statistical redundancy with entropy coding; [0006] The above-mentioned video coding standards all have intra-coded frames, namely I frames, and inter-frame coded frames, namely P frames, and I frames and P frames ado...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04N7/26H04N7/30H04N19/625
CPCG06F17/147
Inventor 虞露张赐勋
Owner XFUSION DIGITAL TECH CO LTD
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com