Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

Phase fraction low moment-based covariance difference propagation algorithm

A fractional low-order, covariance technology, applied in the field of propagation algorithm of covariance difference, can solve the problems of inaccurate classification, large amount of calculation, etc., and achieve the effect of suppressing alpha noise and high parameter estimation accuracy

Active Publication Date: 2021-11-26
HARBIN ENG UNIV
View PDF12 Cites 2 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The object of the present invention is a propagation algorithm based on the covariance difference of the low-order moment of the phase fraction in order to overcome the above-mentioned large amount of calculation and the problem of inaccurate classification caused by using subjective criteria to distinguish the source type

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Phase fraction low moment-based covariance difference propagation algorithm
  • Phase fraction low moment-based covariance difference propagation algorithm
  • Phase fraction low moment-based covariance difference propagation algorithm

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0085]下面结合附图对本发明具体实施方式做进一步说明。

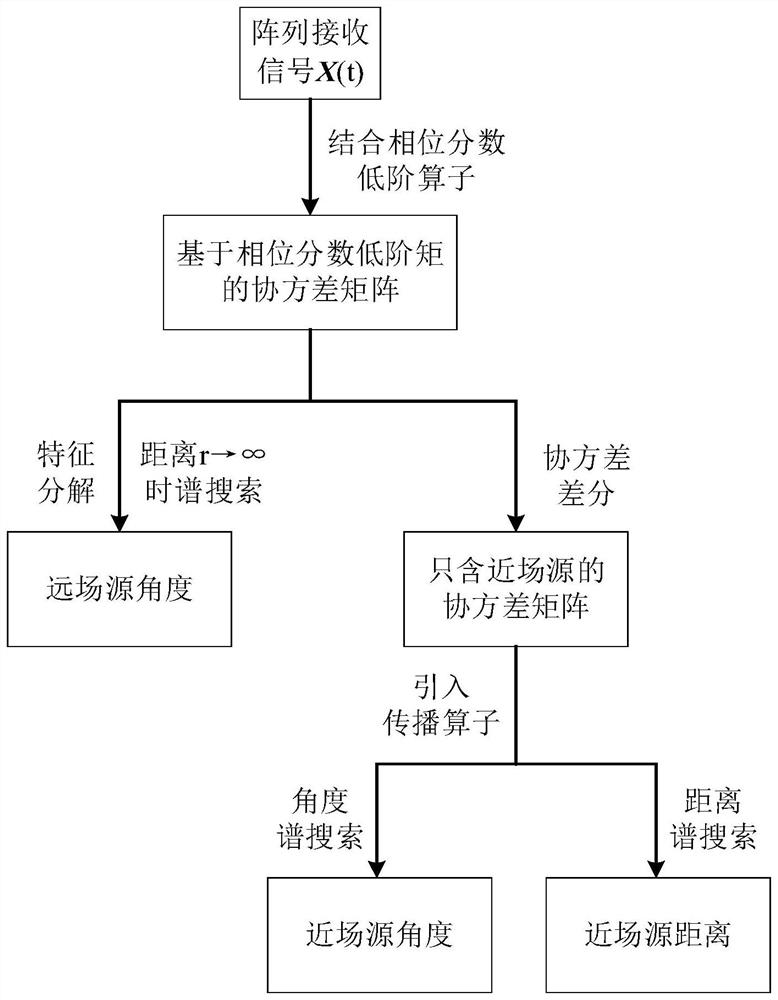
[0086]本发明为一种基于相位分数低阶矩的协方差差分的传播算法，算法框图如图1所示，包括以下几个步骤：

[0087]步骤一：根据阵列信号接收矩阵X(t)求取基于相位分数低阶矩的协方差矩阵RPFLOM；

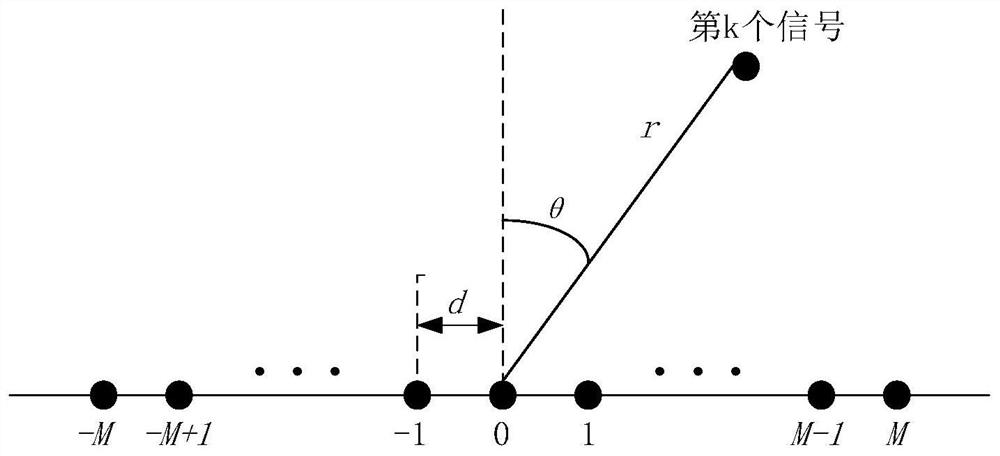
[0088]在图2中，假设有N＝2M+1个阵元的对称均匀线阵(ULA)，以中心位的阵元为相位参考阵元，阵元间距为d，波长为λ，含有K1个近场信号源和K2个远场信号源，则混合信号源个数为K＝K1+K2，信号源的入射方位角为θ，近场源距离为r，远场源距离为∞。则阵列接收远-近场混合信号源定位模型的矢量表示为：

[0089]X(t)＝AS(t)+N(t)＝AfSf(t)+AnSn(t)+N(t) (25)

[0090]

[0091]

[0092]

[0093]

[0094]其中，X(t)是(2M+1)×1维的快拍数据矢量，Af为(2M+1)×K2维的远场源阵列流行矩阵，An为(2M+1)×K1维的近场源阵列流行矩阵，此时的相位参数γk和φk分别为：

[0095]γk＝(-2πdsinθk) / λ (30)

[0096]φk＝πd2cos2θk / λrk (31)

[0097]N(t)是(2M+1)×1维的alpha噪声，即满足对称α稳定(Symmetric Alpha Stable,SαS)分布，其特征函数符合如下形式：

[0098]φ(u)＝exp{jau-γ|u|α[1+jβsgn(u)ω(u,α)]} (32)

[0099]

[0100]

[0101]其中α为特征指数，取值范围为0＜α＜2；γ为分布系数，这里取γ＝1；β为对称参数，这里取β＝0；a为位置参数，这里取a＝0。

[0102]通过X(t)求取基于相位分数低阶矩的协方差矩阵RPFLOM，即

[0103]RPFLOM＝E{XX},0

[0104]其中p为阶数，且p阶相位分数低阶矩的算子为：

[0105]

[0106]其中，*表示向量的共轭。

[0107]现实中是通过对接收信号进行离散采样估计，从而得到估计的协方差矩阵RPFLOM的第ij个元素为：

[0108]

[0109]其中，T是快拍数，xi,xj分别为X(t)的第i行和第j列。

[0110]此时已经抑制了环境中的alpha噪声，因此可以直接对RPFLOM做后续算法处理来估计目标参数。

[0111]步骤二：令距离r→∞，利用...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a phase fraction low moment-based covariance difference propagation algorithm, and mainly solves the problem of parameter estimation of a far-near field mixed signal source of an array radar in an alpha noise environment. The method comprises the following steps: firstly, establishing a model for receiving signals by a uniform and symmetrical array antenna, constructing a covariance matrix based on a phase fraction low-order moment to suppress alpha noise, and performing angle estimation on a far-field source through a MUSIC algorithm; then separating a near-field covariance matrix by combining a covariance difference thought and utilizing structural differences of a far-field covariance matrix, a noise covariance matrix and the near-field covariance matrix; and finally, introducing a propagation operator to solve a noise subspace corresponding to the covariance difference matrix at the moment, and further estimating a near-field source angle parameter and a distance parameter through spectrum peak search. According to the method, the alpha noise is suppressed while certain calculation complexity is reduced, a subjective standard does not need to be used for distinguishing far-near field source types, and the parameter estimation precision is high.

Description

technical field [0001] The invention belongs to the field of array signal processing, and specifically relates to a propagation algorithm based on the covariance difference of the low-order moment of the phase fraction. Background technique [0002] Direction of Arrival (DOA) estimation is one of the important research contents in the field of array signal processing, and is widely used in navigation, communication, sonar, radar and other fields. DOA estimation algorithms can be roughly divided into subspace algorithms and statistical method algorithms. Subspace algorithms include multiple signal classification (Multiple Signal Classification, MUSIC) algorithm, Capon algorithm, and rotation invariant subspace (Estimation of Signal Parameters via Rotational Invariance, ESPRIT) algorithm. Effects of noise subspace evaluation. Statistical method algorithms, such as the Maximum Likelihood (ML) algorithm, use the best fit between the ideal signal model and the observed data to ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S3/14G01S7/295G06F17/16
CPCG01S3/14G01S7/295G06F17/16
Inventor 黄平王伟薛冰杨丽娜
Owner HARBIN ENG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com