Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

One-Dimensional Wave Equation Solving Method Based on Neural Network

A wave equation and neural network technology, applied in neural learning methods, biological neural network models, neural architectures, etc., can solve the time-consuming and labor-intensive problems of one-dimensional wave equations

Active Publication Date: 2022-04-15
HARBIN INST OF TECH
View PDF19 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] The purpose of the present invention is to solve the time-consuming and labor-intensive problem of the neural network in solving the one-dimensional wave equation under different working conditions, and to provide a method for solving the one-dimensional wave equation based on the neural network in multiple working conditions

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • One-Dimensional Wave Equation Solving Method Based on Neural Network
  • One-Dimensional Wave Equation Solving Method Based on Neural Network
  • One-Dimensional Wave Equation Solving Method Based on Neural Network

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

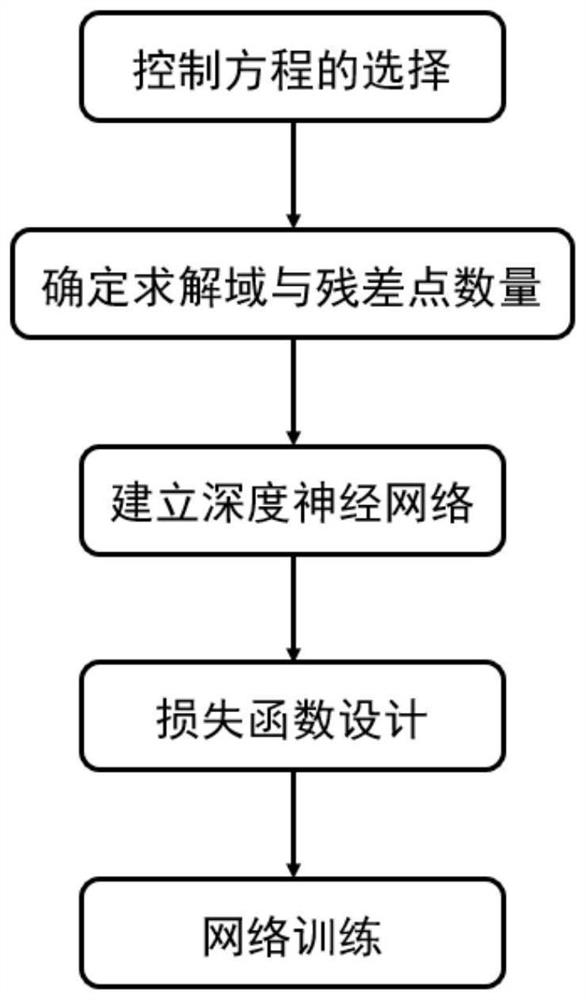
[0052] Specific implementation mode 1: In this implementation mode, the multi-working-condition one-dimensional wave equation solution method based on neural network is implemented according to the following steps:

[0053] Step 1: Establish the governing equation, the one-dimensional seismic wave equation in isotropic media is as follows:

[0054]

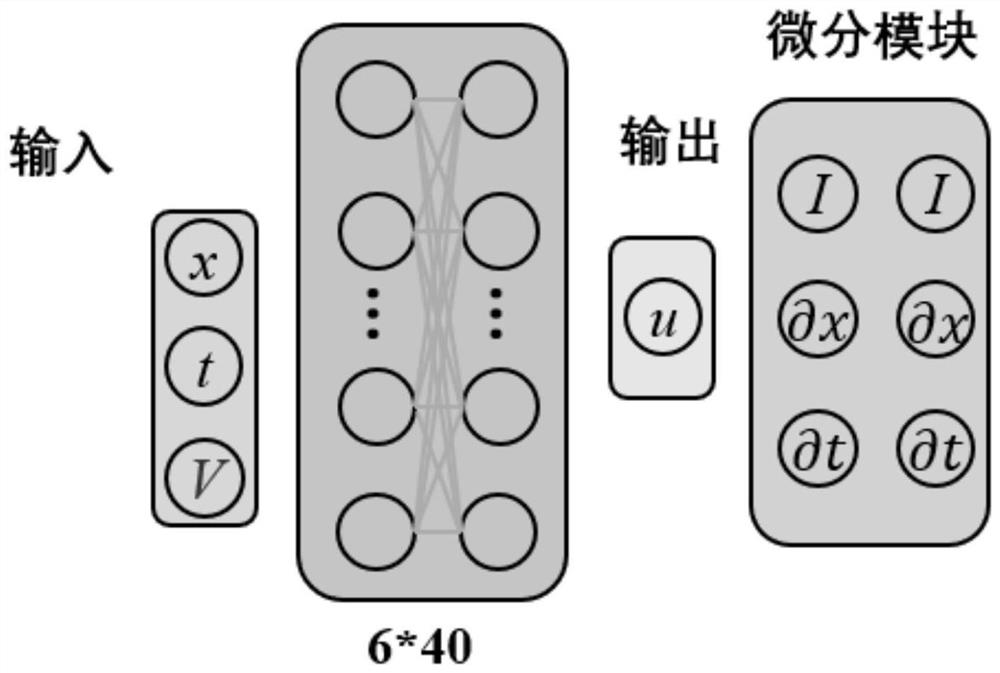
[0055] Among them, V represents the wave velocity, and u represents the displacement of the particle under the (x, t) coordinates;

[0056] Step 2. Determine the solution domain and the number of residual points:

[0057] Set the solution domain of x to [0,1], the solution domain of t to [0,1], and the number of residual points to be 400-800;

[0058] Step 3. Establish a deep neural network:

[0059] Establish a fully connected layer neural network including 6 hidden layers, and use the hyperbolic tangent function (Tanh) as the activation function to obtain a deep neural network model;

[0060] Step 4. Loss function design:

...

specific Embodiment approach 2

[0066] Embodiment 2: This embodiment differs from Embodiment 1 in that the number of residual points in Step 2 is 500.

specific Embodiment approach 3

[0067] Embodiment 3: This embodiment differs from Embodiment 1 or Embodiment 2 in that each hidden layer in Step 3 contains 40 neurons.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for solving one-dimensional wave equations under different working conditions based on a neural network. The invention belongs to the field of earthquake engineering. One-dimensional wave equation solution method: 1. Select the 1-dimensional wave equation as the equation to be solved; 2. Determine the solution domain of input variables and the number of residual points; 3. Establish a fully connected layer neural network including 6 hidden layers; 4. Design a specific loss function; 5. Pre-training and refined training of the neural network. The present invention takes the wave velocity as an input, and proposes a neural network-based one-dimensional wave equation solution method, so that the model can learn the influence of different working conditions on the equation solution. On the premise of maintaining high solution accuracy, the general equation and stress condition The addition of also increases the interpretability of the solution method.

Description

technical field [0001] The invention belongs to the field of earthquake engineering, and in particular relates to a method for solving multi-working-condition one-dimensional wave equations based on a neural network and then realizing earthquake simulation. Background technique [0002] Accompanied by economic development, accelerated urbanization, and the emergence of megacities and urban agglomerations, all of these pose higher challenges to the seismic resilience of individual structures, building groups, and even the entire city. The establishment of the ground motion field is the prerequisite for the design and evaluation of the structural seismic toughness. How to quickly and accurately simulate the earthquake field is also a hot topic in the academic circles. The seismic field is closely related to the propagation of seismic waves in the medium. According to the representation theorem, ground motion can be expressed as the convolution of the Green's function and the...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/13G06N3/04G06N3/08G01V1/36
CPCG06F17/13G06N3/04G06N3/08G01V1/36G01V2210/675
Inventor 籍多发翟长海李晨曦温卫平
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com