Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials

A nonlinear feature and topology optimization technology, applied in design optimization/simulation, CAD numerical modeling, special data processing applications, etc., can solve problems such as large eigenvector errors, inability to explain the degree of influence of frequency-related items, and difficulty in convergence. Achieve stable iterations, promote dynamic performance research, and achieve further upgrade effects

Active Publication Date: 2022-08-05
SHANDONG UNIV
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] A solution method for nonlinear eigenvalues ​​is proposed in the prior art, but this method omits the frequency-dependent term. Although it can be solved directly, it cannot explain the degree of influence of the frequency-dependent term on the result, resulting in inaccurate results
The existing technology also proposes an asymptotic numerical method for solving nonlinear eigenvalue problems. Although this method considers frequency-related items, the eigenvector error of the solution using this method is relatively large, and it is applied to topology optimization. During the iterative process, there will be Difficulty in convergence
In addition, so far, the solution process of nonlinear eigenvalues ​​has not formed a complete set of methods in the field of topology optimization.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials
  • A nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials
  • A nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

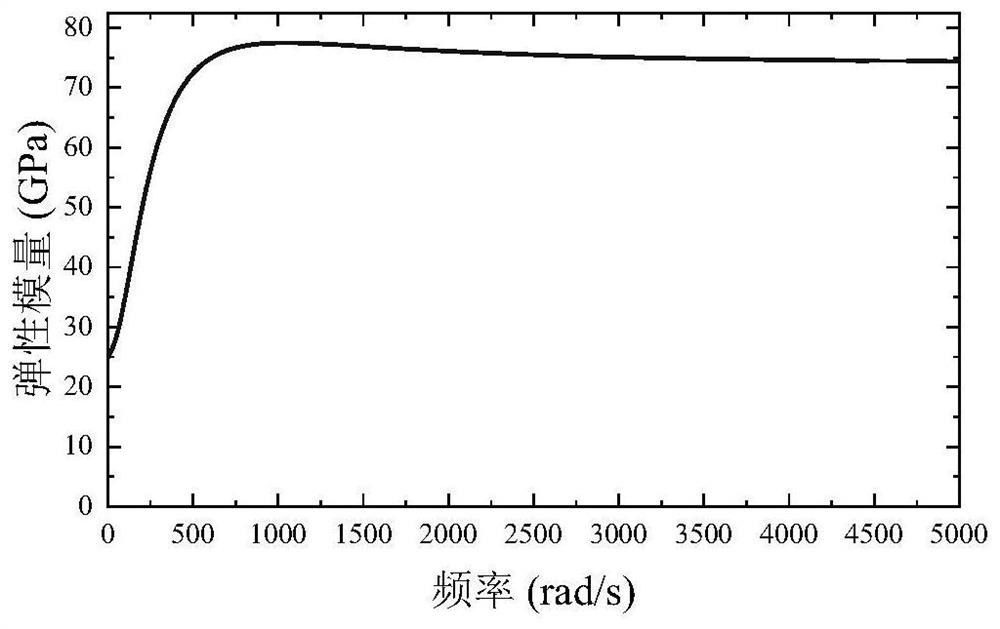
[0052] As mentioned in the background art, most of the methods for solving nonlinear equations disclosed in the prior art omit frequency-dependent terms, or the eigenvectors solved by traditional asymptotic numerical methods have large errors, resulting in convergence in the iterative process after being applied to topology optimization. difficult phenomenon. Therefore, the present invention provides a nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials.

[0053] like figure 1 As shown in the figure, this embodiment provides a nonlinear eigenvalue topology optimization method considering frequency-dependent materials. This embodiment is exemplified by applying the method to a server. It can be understood that this method can also be applied to a terminal. It can also be applied to include terminals, servers and systems, and is realized through interaction between terminals and servers. The server can be an independent physic...

Embodiment 2

[0122] This embodiment provides an application of a nonlinear eigenvalue topology optimization method considering frequency-dependent materials in structural design.

[0123] Nonlinear eigenvalue topology optimization methods for materials considering frequency dependence, including:

[0124] According to the actual working conditions, the structure is divided into meshes and boundary conditions are added, and the corresponding overall stiffness matrix and overall mass matrix in the structure are obtained through finite element analysis;

[0125] The nonlinear eigenvalue equation is constructed based on the corresponding overall stiffness matrix and overall mass matrix in the structure, and the nonlinear eigenvalue equation is solved by the continuous asymptotic numerical method and the inverse iteration method, and the structural eigenfrequency and the modified eigenvector are obtained;

[0126] Taking the maximization of the fundamental frequency of the structure as the goal...

Embodiment 3

[0137] This embodiment provides a nonlinear eigenvalue topology optimization system considering frequency-dependent materials.

[0138] A nonlinear eigenvalue topology optimization system considering frequency-dependent materials, including:

[0139] a matrix acquisition module, which is configured to: divide the structure into meshes according to actual working conditions and add boundary conditions, and obtain the corresponding overall stiffness matrix and overall mass matrix in the structure through finite element analysis;

[0140] a structural eigenfrequency and corrected eigenvector acquisition module, which is configured to: construct a nonlinear eigenvalue equation based on the corresponding overall stiffness matrix and overall mass matrix in the structure, and use a continuous asymptotic numerical method and an inverse iterative method to solve the nonlinear Eigenvalue equation to obtain structural eigenfrequency and modified eigenvector;

[0141] The material amount...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention belongs to the technical field of structural topology optimization, and provides a nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials. The method includes: dividing a mesh into a structure according to actual working conditions and adding boundary conditions; obtaining a corresponding overall stiffness matrix and an overall mass matrix in the structure through finite element analysis; based on the corresponding overall stiffness matrix and overall mass matrix in the structure The nonlinear eigenvalue equation is constructed, and the continuous asymptotic numerical method and the inverse iterative method are used to solve the nonlinear eigenvalue equation to obtain the structural eigenfrequency and the modified eigenvector. The goal is to maximize the fundamental frequency of the structure, and the volume constraint is satisfied as Constraints, combined with the structural eigenfrequency and the corrected eigenvectors, establish a topology optimization model, input the material components containing the frequency-dependent material structure into the model, and obtain the required material amount through topology optimization.

Description

technical field [0001] The invention belongs to the technical field of structural topology optimization, and in particular relates to a nonlinear eigenvalue topology optimization method and system considering frequency-dependent materials. Background technique [0002] The statements in this section merely provide background information related to the present invention and do not necessarily constitute prior art. [0003] Structural eigenvalue topology optimization is a research hotspot in the field of dynamics optimization, and has a wide range of applications in improving the fundamental frequency of structures, avoiding resonance, and designing bandgap materials. However, most of the existing studies assume that the material is an elastic material, and the eigenfrequency of the structure is obtained by solving the linear eigenvalue equation. However, the elastic modulus of many engineering materials is frequency-dependent, that is, the elastic modulus of the material cha...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/23G06F30/18G06F17/13G06F111/04G06F111/10
CPCG06F30/23G06F30/18G06F17/13G06F2111/10G06F2111/04
Inventor 李取浩吴强波刘书田朱向前张风同曲泳鑫
Owner SHANDONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com