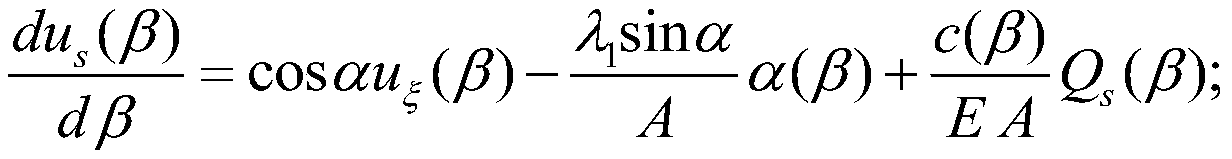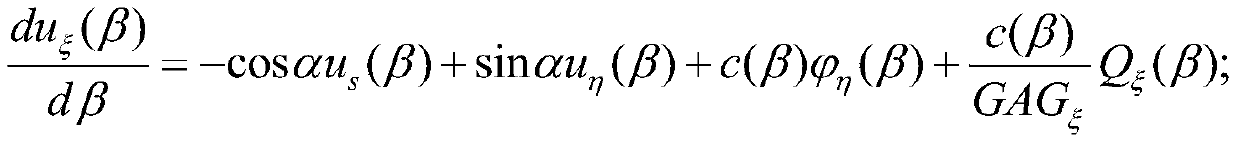Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A method for measuring and calculating the inherent vibration frequency of a convex spring in a nonlinear rectangular cross section

A technology of natural vibration frequency and rectangular cross-section, which is applied in the field of natural vibration frequency measurement and calculation, can solve problems such as large errors in natural vibration frequency, and achieve the effect of accurate and reliable technical means in production and application

Active Publication Date: 2019-06-14
NORTH CHINA UNIV OF WATER RESOURCES & ELECTRIC POWER
View PDF17 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0009] The object of the invention of the present invention is to provide a method for measuring and calculating the natural frequency of the convex spring in the nonlinear rectangular section, to solve the problem of the natural frequency of the convex spring in the nonlinear rectangular section of the narrow and long rectangular section measured and calculated by the existing method. The technical problem of large error in the actual natural vibration frequency

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A method for measuring and calculating the inherent vibration frequency of a convex spring in a nonlinear rectangular cross section
  • A method for measuring and calculating the inherent vibration frequency of a convex spring in a nonlinear rectangular cross section
  • A method for measuring and calculating the inherent vibration frequency of a convex spring in a nonlinear rectangular cross section

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0049] Embodiment 1: a kind of modeling method of measuring the free vibration model of convex spring in nonlinear rectangular section, comprises the following steps:

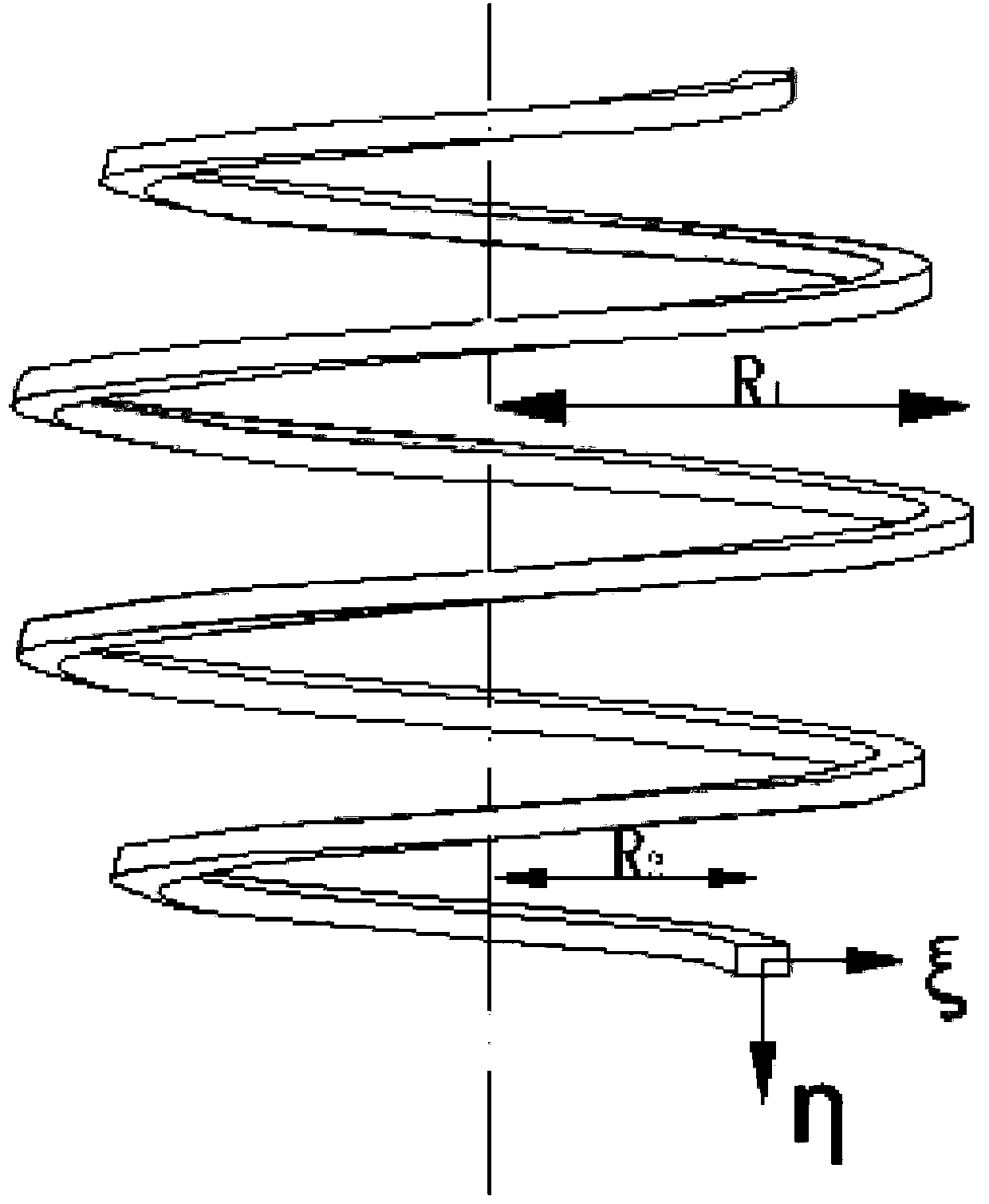
[0050] For a nonlinear convex spring, the geometric relationship of its helix is:

[0051] x=R(β)cosβ, y=R(β)sinβ, z=h(β)β, (4)

[0052] in: h(β)=R(β)tanα, R 1 for the trail, R 2 is the major diameter, n is the number of spiral turns, α is the helix angle, β is the horizontal angle, R(β) is the function of the median diameter of the helix, and h(β) is the function of the pitch of the helix.

[0053] From formula (4), it can be seen that for a nonlinear convex spring, although the helix angle α is constant, its diameter and pitch change, and the helix is ​​a space curve with variable curvature and variable torsion rate, respectively with K η (β)=R(β) / c 2 (β), K s (β)=h(β) / c 2 (β) represents the curvature and torsion of the helix.

[0054] Based on the theory of natural bending and torsion beams, the ...

Embodiment 2

[0075] Embodiment 2: A method for measuring and calculating the natural frequency of the convex spring in a nonlinear rectangular section, measuring the minor diameter R of the convex spring in the nonlinear rectangular section 1 , large diameter R 2 , the number of helical turns n, the helix angle α of the spring, the width of the centroidal axis ξ direction of the spring wire cross section, the height of the centroidal axis η direction of the spring wire cross section, the density ρ of the spring wire material, and the spring wire material The elastic modulus E of the spring wire material, the shear modulus G of the spring wire material, and the shear shape coefficient G of the cross-sectional centroid axis ξ of the spring wire ξ , the shear shape factor G in the direction of the main axis η of the centroid of the cross section of the spring wire η ;Use the small diameter R of the convex spring 1 , large diameter R 2 , the number of helical turns n, the helical angle α of...

Embodiment 3

[0105] Embodiment 3: a method for measuring and calculating the natural frequency of the convex spring in the nonlinear rectangular cross-section in Embodiment 1, the centroid axis ξ direction of the cross-section of the spring wire corresponds to the width direction of the rectangular cross-section, and the The width of the rectangular section of the convex spring in the nonlinear rectangular section is 2a, the height is 2b, and a:b≤0.6. The natural vibration frequency includes at least one of the first, second, third, fourth and fifth vibration frequencies of the convex spring with a nonlinear rectangular section. It works better for the first frequency of vibration of a convex spring in a nonlinear rectangular section.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for measuring and calculating the inherent vibration frequency of a convex spring in a nonlinear rectangular cross section. The method considers the influence of the warping effect on the inherent vibration frequency, wherein a free vibration model is shown as a formula, and the method comprises the steps of measuring the density p of the small-diameter R1, the large-diameter R2, the number of spiral turns n, the spiral angle alpha, the centroid main shaft eta of the cross section of the reed wire, the centroid main shaft e of the cross section of the reed wireand the reed wire material p of the spring; the elastic modulus E of the reed wire material, the shear modulus G of the reed wire material, the shear shape coefficient G e on the cross section centripetal main shaft e of the reed wire and the shear shape coefficient G eta on the cross section centripetal main shaft eta of the reed wire; and calculating to obtain the inherent vibration frequency omega of the convex spring. The error between the measured inherent vibration frequency and the actual inherent vibration frequency is smaller than that of an existing method.

Description

technical field [0001] The invention relates to the technical field of spring applications, in particular to a method for measuring and calculating the natural vibration frequency of a convex spring with a nonlinear rectangular section. Background technique [0002] A spring is a mechanical component that uses the elasticity and structural characteristics of the material to deform during work, transforming mechanical work or kinetic energy into deformation energy, or transforming deformation energy into mechanical work or kinetic energy. Its functions include mitigating shock or vibration, such as the supporting spring of the crusher or the suspension spring of the vehicle, etc.; mechanical energy storage, such as the original spring on the clock, instrument or automatic control mechanism; controlling movement or force, such as the valve, Springs on clutches, control valves, brakes, and various regulators; force-measuring devices, such as springs on spring scales and dynamom...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
CPCY02T90/00
Inventor 郝颖
Owner NORTH CHINA UNIV OF WATER RESOURCES & ELECTRIC POWER
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com