Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A time-varying event trigger filtering method with data loss under an unknown probability condition

A technology of data loss and event triggering, which is applied to electrical components, digital technology networks, impedance networks, etc., can solve the problems affecting filter performance, data loss and random non-linearity of unknown probability, and event triggering mechanism that cannot be dealt with at the same time. Achieve the effect of easy solution and realization, and relative error reduction

Active Publication Date: 2019-05-07
HARBIN UNIV OF SCI & TECH
View PDF12 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] The purpose of the present invention is to solve the problem that the existing filtering method cannot simultaneously deal with data loss of unknown probability, random nonlinearity and event trigger mechanism, thereby affecting the performance of the filter, and proposes a time-varying event with data loss in the case of unknown probability trigger filtering method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A time-varying event trigger filtering method with data loss under an unknown probability condition
  • A time-varying event trigger filtering method with data loss under an unknown probability condition
  • A time-varying event trigger filtering method with data loss under an unknown probability condition

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

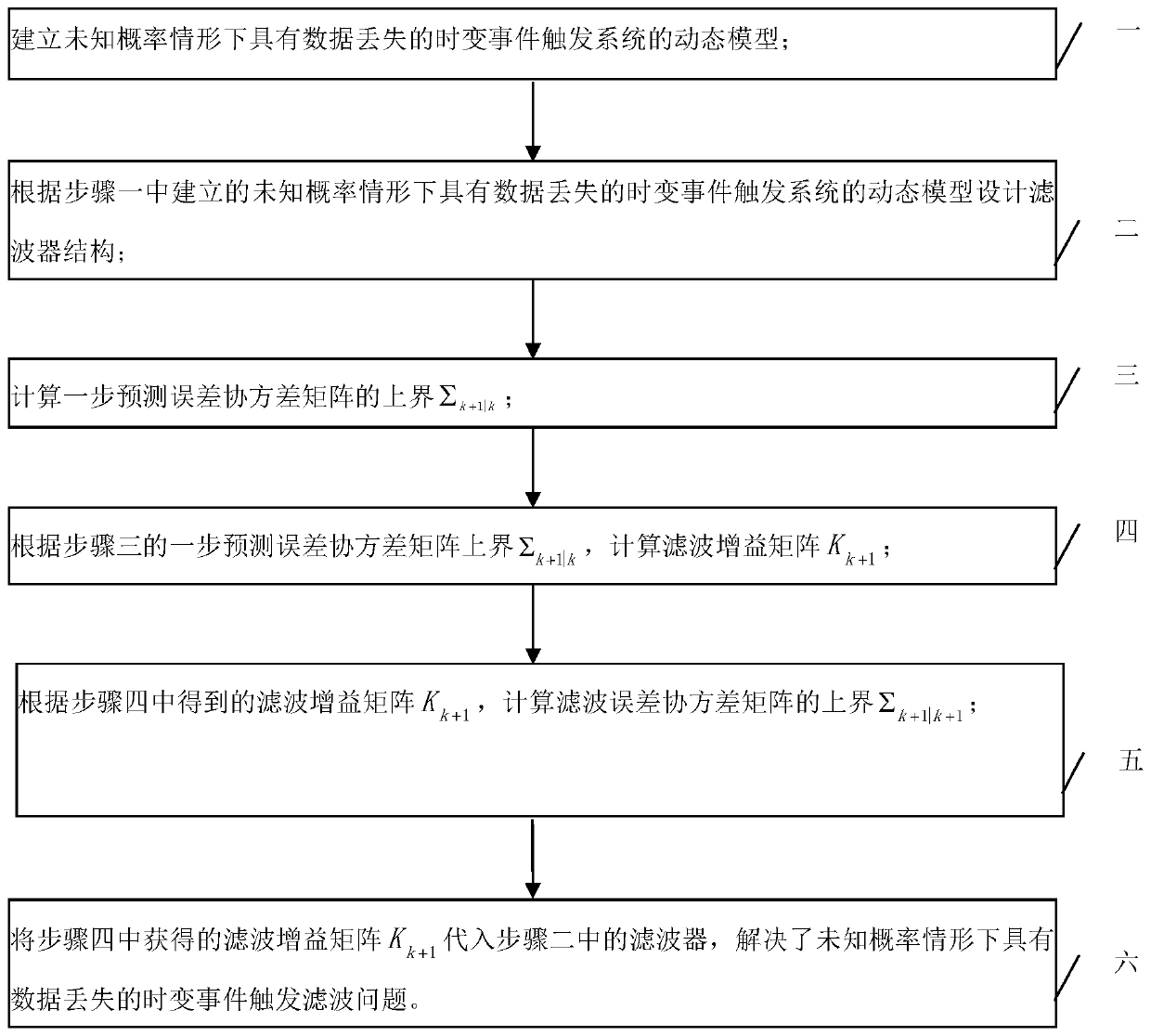
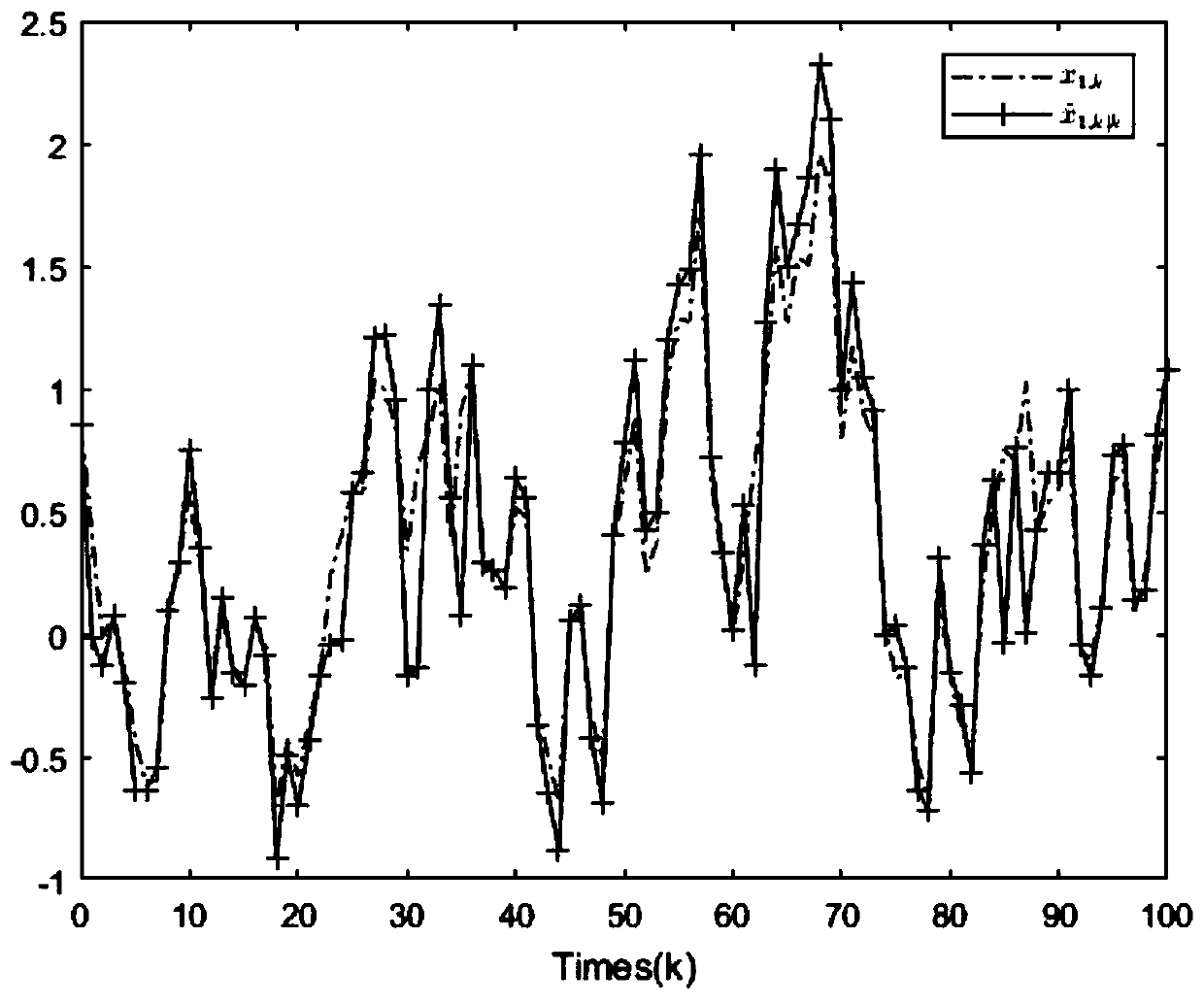
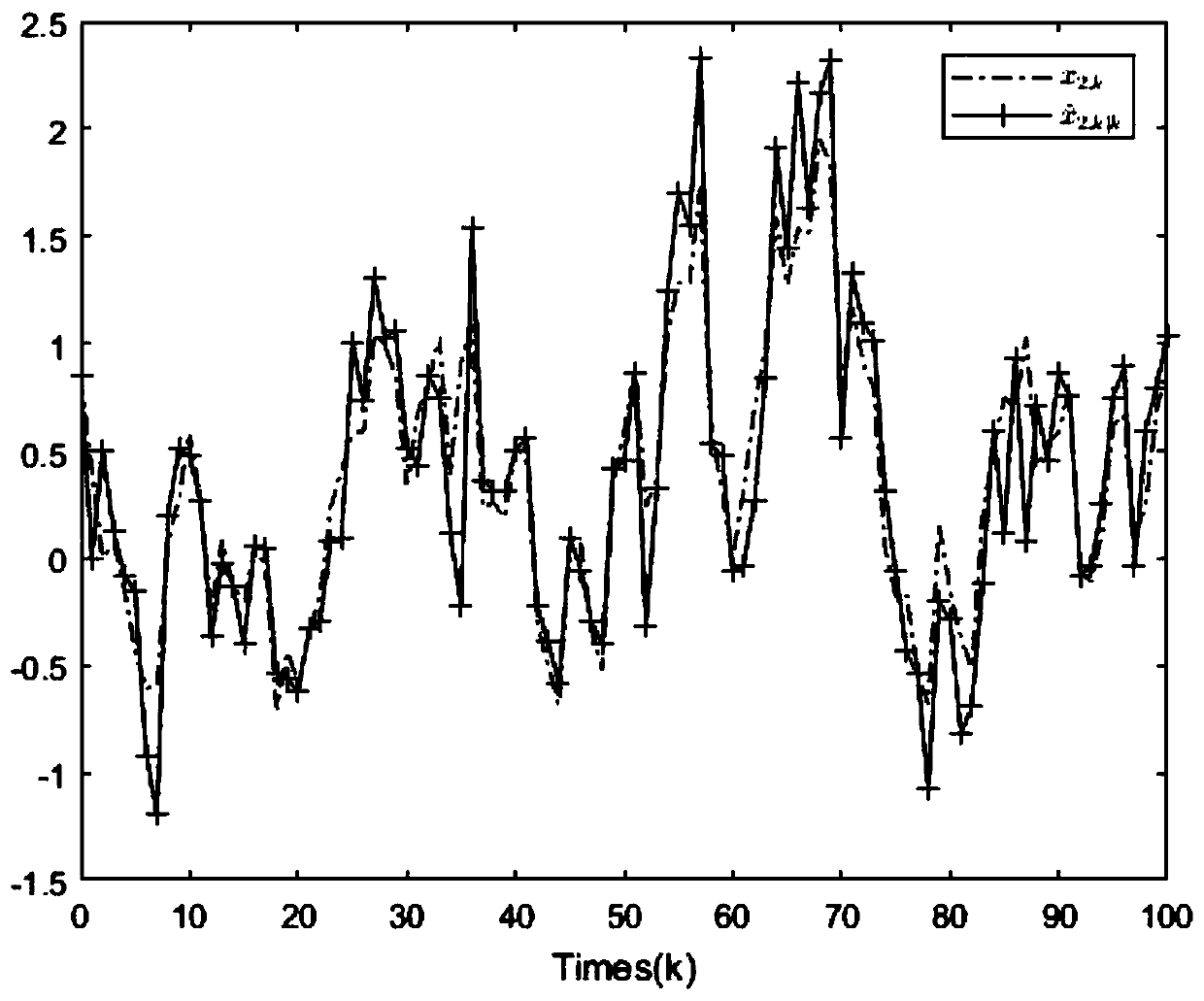
[0021] The time-varying event-triggered filtering method with data loss under the unknown probability situation of this embodiment, the method includes the following steps:

[0022] Step 1. Establishing a dynamic model of a time-varying system with unknown probability of data loss, stochastic nonlinearity, and event-triggered mechanism;

[0023] Step 2. Design the structure of the filter according to the dynamic model of the time-varying system with unknown probability of data loss, random nonlinearity and event trigger mechanism established in step 1;

[0024] Step 3, calculating the upper bound of the one-step prediction error covariance matrix of the dynamic model at time k;

[0025] Step 4, according to the upper bound of the one-step prediction error covariance matrix in step 3, calculate the filter gain matrix at k+1 moment;

[0026] Step 5. Substituting the gain matrix at time k+1 obtained in step 4 into the filter equation in step 2 to obtain an estimate at time k+1 ...

specific Embodiment approach 2

[0028] The difference from the first embodiment is that the time-varying event-triggered filtering method with data loss in the case of unknown probability in this embodiment, in the first step, the established data loss with unknown probability, random non-linearity and event-triggered filtering method The state-space form of the dynamic model of the time-varying system of the mechanism is:

[0029] x k+1 =(A k +ΔA k )x k +α k f(x k )+B k ω k (1)

[0030] the y k =λ k C k x k +ν k (2)

[0031] where x k is the state variable of the system at time k, y k is the measurement output; f(x k ) is a nonlinear continuous differentiable function; ω k is mean zero variance Q k process noise; ν k is mean with zero variance for R k measurement noise; A k is the system matrix, C k is the measurement matrix at time k, B k is the noise distribution matrix; ΔA represents the unknown of the system, and satisfies the norm bounded uncertainty, ΔA=M 1 f 1,k N 1 ,M 1 ...

specific Embodiment approach 3

[0035] The difference from the second specific embodiment is that the time-varying event-triggered filtering method with data loss in the case of unknown probability in this embodiment, in the above-mentioned step 2, according to the data loss with unknown probability established in step 1, random The process of designing filters for dynamic models of time-varying systems with linear and event-triggered mechanisms, specifically:

[0036] First, select the following event trigger formula:

[0037]

[0038] In the formula, Indicates the measurement output at the trigger moment of the latest event, δ indicates the known adjustment threshold and δ>0, express the transpose of y k+l Indicates the measured value at the current moment, then the actual output of the system at time k is as follows:

[0039]

[0040] is the actual output value at time k, k i Indicates the initial trigger moment;

[0041] Then, design the filter:

[0042]

[0043]

[0044] In the for...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a time-varying event trigger filtering method with data loss under an unknown probability condition, and belongs to the field of control systems. An existing filtering method cannot process data loss with unknown probability, random nonlinearity and an event triggering mechanism at the same time, and the performance of a filter is affected. The method comprises the following steps: establishing a dynamic model of a time-varying system with an unknown probability of data loss, random nonlinearity and an event triggering mechanism; Designing a filter according to the established time-varying system dynamic model; Calculating the upper bound of the one-step prediction error covariance matrix of the filter; Calculating a filtering gain matrix; Calculating the upper bound of the filtering error covariance matrix; And substituting the obtained filtering gain matrix into a designed filter to obtain a data loss, random nonlinearity and event trigger mechanism filter with unknown probability. The method can simultaneously process data packet loss with unknown probability, random nonlinearity and an event trigger mechanism, achieves the purpose of nonlinear disturbance, and is easy to solve and implement.

Description

technical field [0001] The invention relates to a time-varying event-triggered filtering method with data loss in an unknown probability situation. Background technique [0002] Filtering is the operation of filtering out the frequency of a specific band in the signal, and it is a basic and important measure for selecting signals and suppressing interference. Filtering is an important research problem in control systems, and it is widely used in signal estimation tasks in radar ranging, target tracking systems, image acquisition and other fields. Due to data redundancy and channel bandwidth limitations, when data is transmitted to the filter end through the network, it usually leads to some network-induced phenomena, such as network congestion, delay, etc., and it is necessary to design a filtering algorithm that adapts to these network-induced phenomena. . [0003] Filtering is an important research problem in control systems, and it is widely used in signal estimation ta...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03H17/02
Inventor 胡军高铭张红旭贾朝清计东海高萍萍
Owner HARBIN UNIV OF SCI & TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com