Remaining Life Prediction Method for Long-Range Correlation Degradation Process Depending on Time and State
A life prediction and time technology, applied in design optimization/simulation, instrumentation, calculation, etc., can solve problems such as difficult parameter estimation, difficult to obtain first-arrival time distribution, and inability to write likelihood functions, etc., to achieve accurate estimation results Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0046] Below in conjunction with accompanying drawing and specific embodiment the present invention is described in further detail:
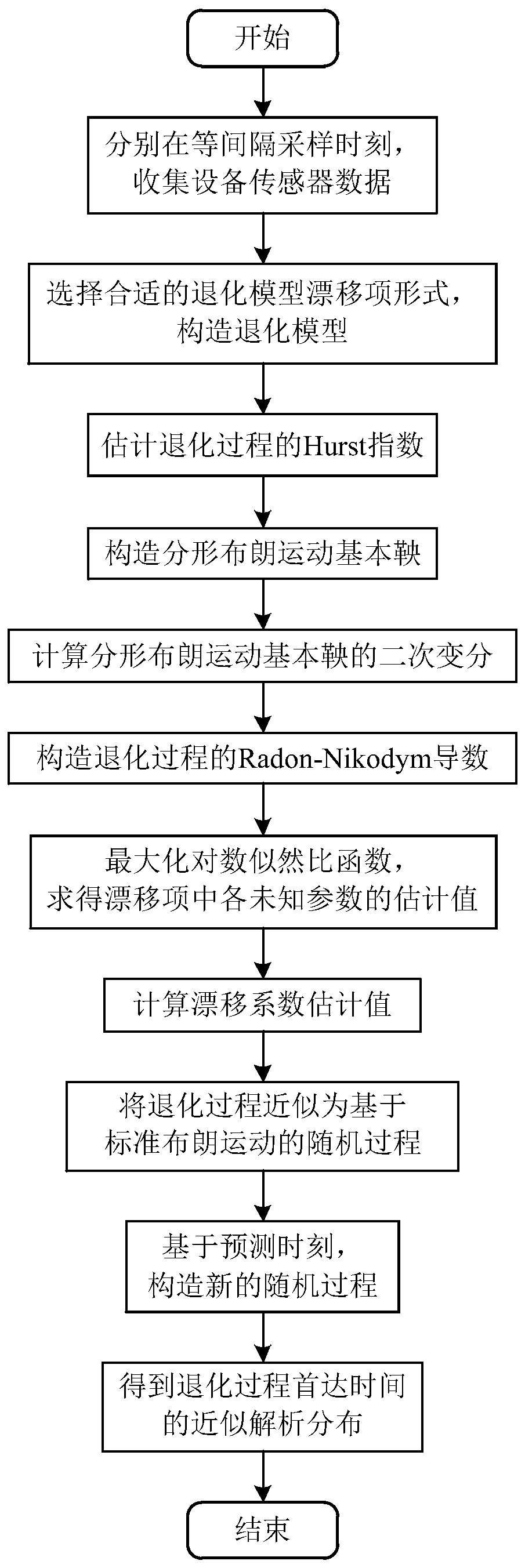
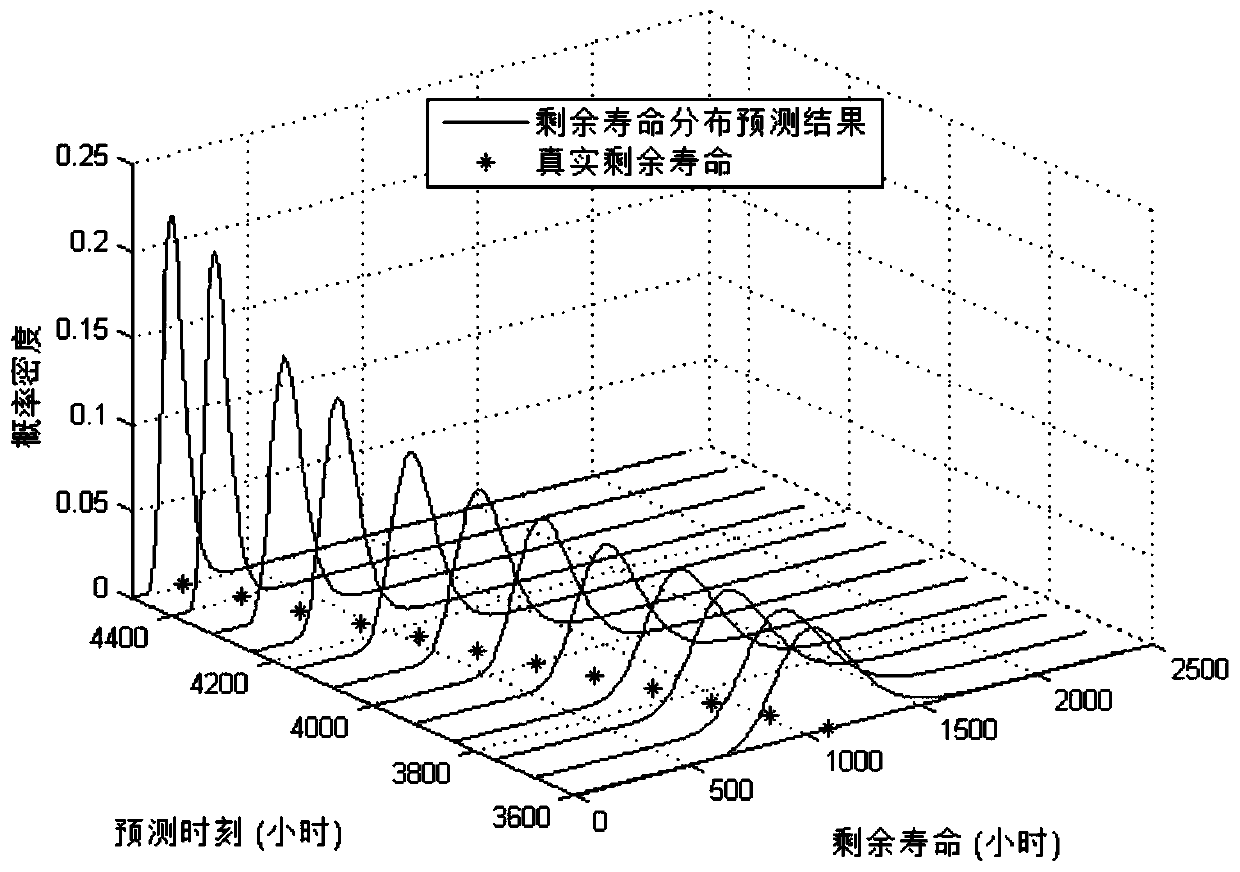
[0047] A method for predicting the remaining life of a long-range correlation degradation process dependent on time and state proposed by the present invention, the process is as follows figure 1 Shown:
[0048] Step 1: Sampling time t at equal intervals respectively 0 ,t 1 ,t 2 ,...,t k , collect temperature sensor data inside the blast furnace wall x 0 ,x 1 ,x 2 ,...,x k , where k is the number of samples;
[0049] Step 2: Establish a degradation model based on fractal Brownian motion based on the collected temperature sensor data characteristics inside the blast furnace wall, as shown in formula (1):
[0050] dX(t)=μ[X(t),t; θ]dt+σ H dB H (t)(1);
[0051]Among them, X(t) is the degradation process, μ[X(t),t;θ] is the coefficient of the drift term, θ is a vector composed of unknown parameters contained in the coefficient of the dri...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - Generate Ideas
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com