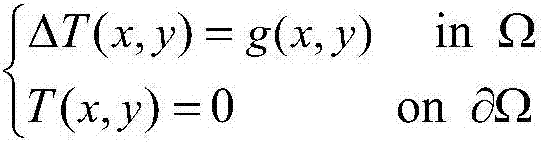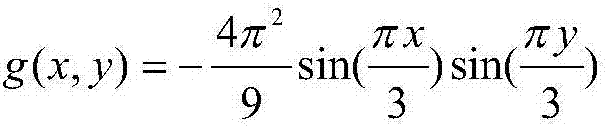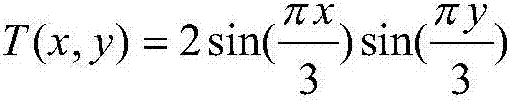Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Computational Domain Optimization Method for Isogeometric Analysis Driven by Local Errors in CAD Models

An isogeometric analysis and error-driven technology, applied in computing, special data processing applications, instruments, etc., to achieve the effect of broadening the application range and improving the efficiency of simulation

Active Publication Date: 2017-06-23
广西鸿运设计有限公司
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, since this method needs to optimize all internal control vertices, it is only suitable for the case where the computational domain is a simple shape

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Computational Domain Optimization Method for Isogeometric Analysis Driven by Local Errors in CAD Models
  • Computational Domain Optimization Method for Isogeometric Analysis Driven by Local Errors in CAD Models
  • Computational Domain Optimization Method for Isogeometric Analysis Driven by Local Errors in CAD Models

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0025] The calculation domain optimization method of isogeometric analysis driven by local error in CAD model, the specific steps are as follows:

[0026] Step 1. In the CAD model, initially parameterize the plane B-spline in the two-dimensional computational domain Ω σ(u,v)={(u,v)|0≤u≤15,0≤v≤15};

[0027] Step 2. Calculate the two-dimensional Poisson equation by using the isogeometric analysis method

[0028]

[0029] Approximate solution of

[0030] The source function of the two-dimensional Poisson equation is:

[0031]

[0032] Has an exact solution in the computational domain [3a,3b]×[3c,3d]

[0033]

[0034] Where a, b, c, and d are all integers, and a, b, c, and d are not 0 at the same time.

[0035] Step 3. Calculate the local error indicator e on each sub-surface in the two-dimensional computational domain Ω S =0.05,0.87,0.23,0.85,0.18,0.74,1.35,2.35,2.67,0,245,2.56,2.69,0.559,1.756,2.456,0.786;

[0036] Step 4, using the average value labeling algorit...

Embodiment 2

[0039] The calculation domain optimization method of isogeometric analysis driven by local error in CAD model, the specific steps are as follows:

[0040] Step 1. In the CAD model, initially parameterize the plane B-spline in the two-dimensional computational domain Ω σ(u,v)={(u,v)|0≤u≤6,0≤v≤6};

[0041] Step 2. Calculate the two-dimensional Poisson equation by using the isogeometric analysis method

[0042]

[0043] Approximate solution of

[0044] Step 3. Calculate the local error indicator e on each sub-surface in the two-dimensional computational domain Ω S ,

[0045] e S =0.08,0.94,0.33,0.95,2.86,1.07,1.80,2.53,2.87

[0046] Step 4, using the average value labeling algorithm to determine the set of sub-patches to be optimized in the two-dimensional computational domain Ω;

[0047] Step 5. Use the adaptive h-r type thinning algorithm to solve the optimal parameterization of the two-dimensional computational domain Ω: for each marked sub-patch, at the midpoint of ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a local error driving isogeometric analysis computational domain self-adaptive optimization method. An isogeometric analysis method requires the optimization on all internal control top points, so the isogeometric analysis method is only applicable to a condition that a computational domain is in a simple shape. According to the method, firstly, a residual method is utilized for obtaining a local error indicator on a computational domain sub chip; then, a control top point set to be optimized is determined according to a local marking strategy; the optimum distribution of the marked internal control top points is obtained through marking the error indicator on a curve chip; a self-adaptive (h-r) type refinement algorithm is provided on the basis of a self-adaptive r type refinement algorithm; and the optimum parameterization of the computational domain is obtained. The method has the advantages that the simulation emulation efficiency and the isogeometric analysis solving precision are improved; the r type refinement algorithm can be applied to CAD models with complicated geometrical shapes; and the application range of the isogeometric analysis method is widened.

Description

technical field [0001] The invention belongs to the field of computer-aided design and engineering, and relates to a simulation technology for realizing the seamless fusion of geometric data in the CAD / CAE stage, in particular to an adaptive optimization method for isogeometric analysis calculation domain driven by local errors. Background technique [0002] In recent years, with the increasing complexity of product design and the increasing precision requirements of advanced manufacturing, how to realize the seamless integration of product design and simulation analysis has become an urgent problem in the CAD / CAE field and has become a research hotspot. [0003] In order to solve this problem, T. Hughes, an academician of the American Academy of Sciences, proposed the "isogeometric analysis" method in 2005, which opened up new ideas for the unified representation of geometric data models in the CAD / CAE stage. The core idea of ​​this method is It is to use the same spline mo...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/50
Inventor 徐岗朱亚光邓立山王毅刚
Owner 广西鸿运设计有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com