Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Fluid simulation method based on inter-belt finite element and Lagrange coordinate

A fluid simulation, finite element technology, used in special data processing applications, instruments, electrical digital data processing, etc.

Active Publication Date: 2015-01-28
DALIAN UNIV OF TECH
View PDF3 Cites 11 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] Aiming at the deficiencies of the prior art, the present invention proposes a simulation analysis method for analyzing two-dimensional incompressible fluids. This method combines the Lagrangian coordinate method with the boundary band finite element method to solve the motion simulation problem of incompressible fluids. The purpose is to Utilize the high precision of the bounded finite element and the convenient processing of the lower boundary of the Lagrangian coordinates, and the advantages of good versatility to improve the calculation efficiency and accuracy of the analysis

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Fluid simulation method based on inter-belt finite element and Lagrange coordinate
  • Fluid simulation method based on inter-belt finite element and Lagrange coordinate
  • Fluid simulation method based on inter-belt finite element and Lagrange coordinate

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0054] Specific Embodiment 1: This embodiment is used to analyze the motion simulation problem of nonlinear incompressible fluid.

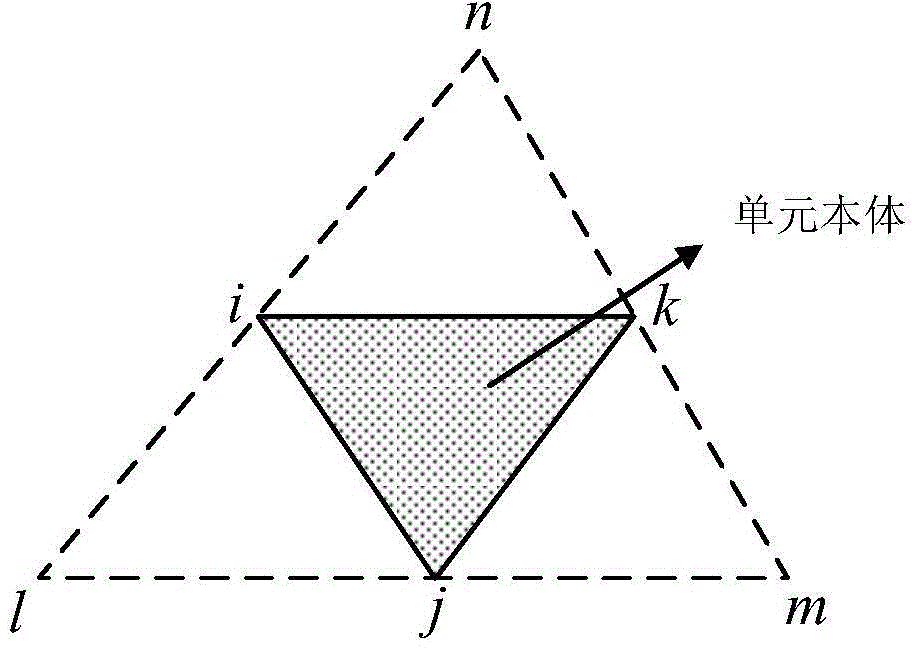
[0055] (a) Divide the computational domain Ω of the fluid into N e units, each unit is Ω i ;

[0056] (b) in unit Ω i The interpolation field of the flow function ψ(x,y) is established on the above. in unit Ω i is the body, the unit Ω i The surrounding units are regarded as the boundary zone of the unit, and the nodes of these units are interpolated together to construct the unit Ω i The interpolation function above, the specific format of the interpolation function is:

[0057] ψ(x,y)=N T ψ i ,N T =p T (x,y)P -1

[0058] in

[0059] p T (x,y)=(1,x,y,x 2 ,xy,y 2 ,…)

[0060] P T =[p(x 1 ,y 1 ),p(x 2 ,y 2 ),…,p(x N ,y N )]

[0061] ψ T =(ψ(x 1 ,y 1 ),ψ(x 2 ,y 2 ),…,ψ(x N ,y N ))

[0062] N T is the shape function vector. (x j ,y j ) is the node coordinates of the boundary zone unit, a total of N, including the u...

specific Embodiment approach 2

[0087] Embodiment 2: This embodiment is used for the simulation analysis of linear incompressible fluids. The difference from Embodiment 1 lies in step (e). At this time, the nonlinear stiffness matrix part is not considered, and a linear dynamic differential equation can be obtained. At this time, the differential equation solving software is used to solve the linear differential equation, and the flow function of each particle at different moments in the linear case can be obtained, and the rest of the steps are the same.

specific Embodiment approach 3

[0088] Embodiment 3: This embodiment is used to analyze the vibration modes of incompressible fluids. The difference from Embodiments 1 and 2 lies in steps (e), (f), (g) and (h), which are not considered at this time. In the nonlinear stiffness matrix part, the eigenvalue problem is obtained:

[0089] K l ψ=ω 2 Mψ

[0090] where ω is the vibration frequency of the fluid. To solve the eigenvalue equation, existing software can be used, such as SIPESC software developed by Dalian University of Technology. According to the flow function mode ψ and the displacement expression given in step (c) in the first embodiment, the displacement of each particle in the fluid is obtained. Using the finite element post-processing program (such as SIPESC.POST, Jifex and other software developed by Dalian University of Technology), the vibration mode of the fluid can be obtained.

[0091] Simulation example: using the method of the present invention, the propagation of solitary waves in a c...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides an incompressible fluid simulation analysis method based on an inter-belt finite element and a Lagrange coordinate. The incompressible fluid simulation analysis method comprises the following steps: dividing a computational domain [omega] of two-dimensional incompressible fluid into Ne units according to a traditional finite element mesh, wherein each unit is [omega i]; and constructing a displacement interpolation field of the unit [omega i], constructing a dynamic differential equation of the fluid according to the displacement interpolation field, and solving the dynamic differential equation to obtain each physical parameter of the fluid so as to carry out the kinematic analysis of the fluid. The invention is characterized in that the displacement interpolation field is constructed by utilizing an inter-belt finite element method, and the dynamic differential equation of the fluid is obtained on the basis of a descriptive method of the Lagrange coordinate. The descriptive method of the Lagrange coordinate is combined with the finite element method to solve a problem of the motion simulation of incompressible fluid, and the invention aims to improve the calculation efficiency and precision of analysis by utilizing the advantages of the high precision of the inter-belt finite element and convenience in lower boundary processing and good universality of the Lagrange coordinate.

Description

technical field [0001] The invention relates to a fluid simulation analysis technology, and constructs a fluid simulation method based on boundary band finite elements and Lagrangian coordinates. Background technique [0002] Fluid simulation analysis is widely used in various engineering fields, such as hydraulic engineering, aviation flight, high-speed train, etc. Theoretically, there are mainly two types of fluid simulation analysis, Euler coordinates and Lagrangian coordinates. From the perspective of numerical analysis methods, there are mainly two types: finite difference method and finite element method. Among them, the finite difference method uses a regular rectangular grid, so the simulation analysis of the fluid in the irregular body needs to refine the grid, which leads to a substantial increase in the amount of calculation. The finite element method is widely used in the simulation analysis of solid structures. The characteristic of this method is that it is su...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
Inventor 吴锋徐小明陈飙松钟万勰
Owner DALIAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com