Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Judgment method for carrying out affine equivalence on two Boolean functions of any variable

A technology of Boolean functions and determination methods, which is applied in the fields of digital integrated circuits and cryptography, can solve problems such as the determination of the affine equivalence of Boolean functions and the selection of representative elements, which are not given, so as to reduce the workload and enrich the The effect of the function

Active Publication Date: 2015-01-21
UNIV OF ELECTRONICS SCI & TECH OF CHINA
View PDF0 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0011] The affine classification of Boolean functions with the above method has the following disadvantages: First, this method does not provide a method for determining whether two Boolean functions are affine equivalent for any number of variables n
[0013] The affine classification of Boolean functions with the above method has great limitations, because this method is aimed at a special class of Boolean functions, and only obtains the necessary and sufficient conditions for the affine equivalence of MRS functions twice, and for 3 times and 4 times, only the affine classification of Boolean functions with part of the number of variables has been obtained, and it has not solved the determination of the affine equivalence of Boolean functions of any variable and the selection of representative elements, nor has it resolved the affine classification of any number of variables for a certain variable. Judgment of affine equivalence of Boolean functions and selection of representative elements

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Judgment method for carrying out affine equivalence on two Boolean functions of any variable
  • Judgment method for carrying out affine equivalence on two Boolean functions of any variable
  • Judgment method for carrying out affine equivalence on two Boolean functions of any variable

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

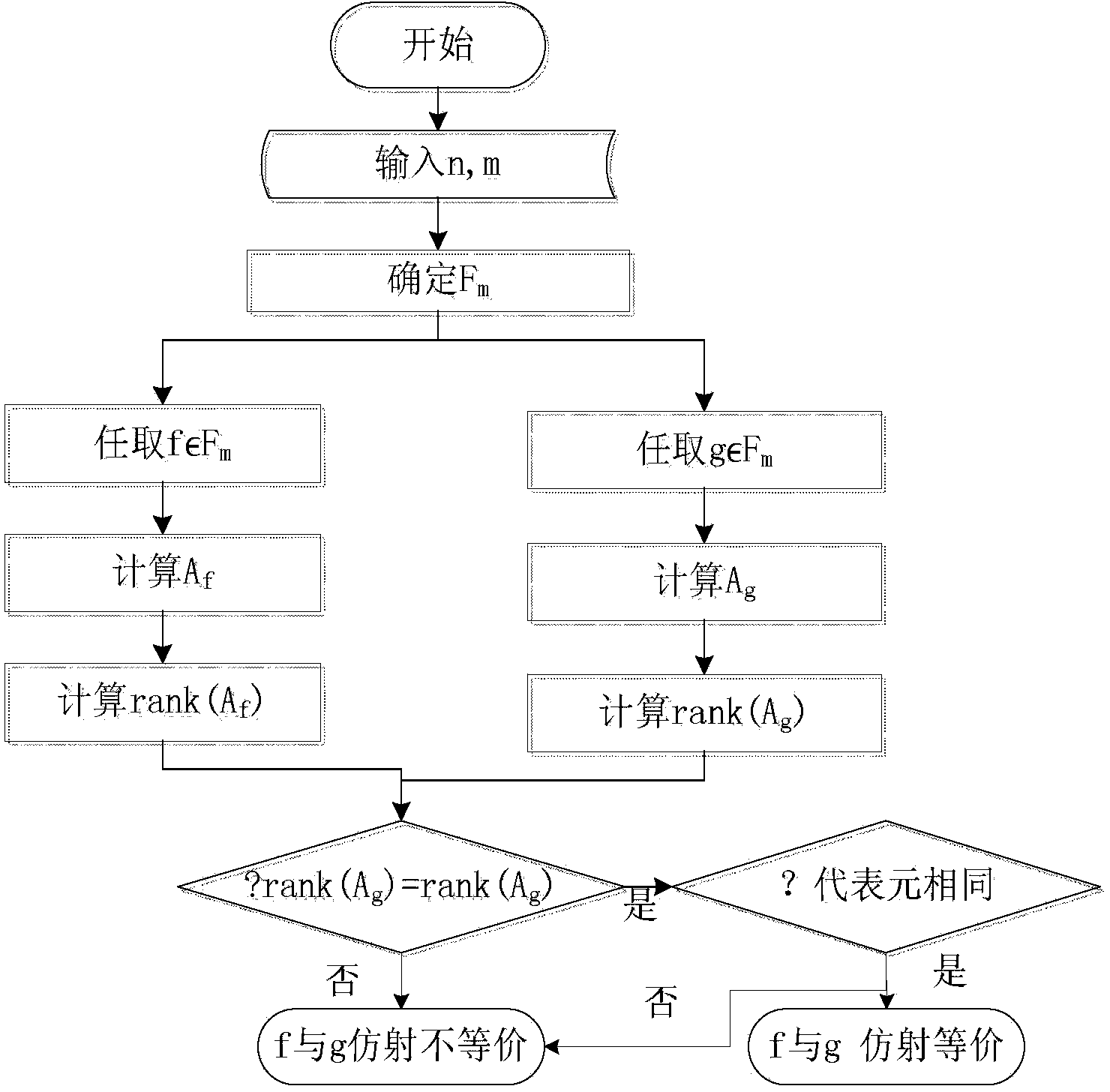
[0036] Embodiment 1 Determine whether two Boolean functions are affine equivalent

[0037] according to figure 1 , taking n=3 as an example, the set of Boolean functions containing 4 1s is set to F 4 , for F 4 For any two Boolean functions f and g in , the truth table is shown in Table 1, and the corresponding variable value matrix is ​​shown in formula (1). And abbreviate f and g as: f=(0,1,1,0,1,1,0,0), g=(1,1,0,0,0,0,1,1).

[0038] Table 1: Truth tables for f and g

[0039] X 1 X 2 X 3 f g 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 0 1 1 0 0 1 1 1 1 0 1

[0040] A f = 0 0 1 0 1 0 ...

Embodiment 2

[0049] Embodiment 2 Select the representative element of the same equivalence class

[0050] For steps 4 and 5, follow the figure 1 In the process of , taking the case of n=3 as an example, when m=4, select the representative element of each affine equivalence class in F4.

[0051] Let the set of Boolean functions similar to f be denoted as M f ,M f The representative element r in f The selection method is as follows:

[0052] Put the matrix A corresponding to f f Carry out a series of elementary column transformations, put A f Matrixize to R f , such as formula (4), then R f The corresponding Boolean function is the representative element of this kind of affine-equivalent Boolean function.

[0053] R f = 0 0 0 0 0 ...

Embodiment 3

[0059] Embodiment 3 Application in combinational logic circuits

[0060] Taking the Boolean function of 4 variables as an example, when m=7, the representative element of the Boolean function is determined by the above method such as image 3 shown, according to Figure 4 A circuit Ci can be designed for each representative element ri, where r1=(1,1,1,1,1,1,1,0,0,0,0,0,0,0,0 ,0), r2=(1,1,1,1,1,1,0,0,1,0,0,0,0,0,0,0), r3=(1,1,1,1 ,1,0,0,0,1,0,0,0,1,0,0,0). Here take r2 as an example to design circuit C such as Figure 7 , after simplification according to the truth table of r2, the CNF expression of r2 is r2=x1’x2’+x1’x2x3’+x1x2’x3’x4’.

[0061] The circuit realization of the affine equivalent Boolean function f=(1,1,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0) can be achieved by The linear combination of the input gate circuits is obtained, where f=x1'x2'+x1x2'x3'+x1'x2x3'x4'. Obtain the affine transformation (A, b) formula (6) according to f=r2(AX+b) as follows:

[0062] ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a judgment method for carrying out affine equivalence on two Boolean functions of any variable and belongs to the field of digital integrated circuits and cryptography. The method includes the first step of determining the Boolean functions Fm, the second step of obtaining a corresponding variable value matrix for any two Boolean functions, the third step of calculating rank (Af) and rank (Ag), and the fourth step of judging whether rank (Af) is the same with rank (Ag) or not and whether representation elements are the same or not, if yes, the affine f and the affine g are equivalent, or the affine f and the affine g are not equivalent. The judgment method can be applied to combinational logic circuits, programmable logic units of an FPGA, and Reed-Muller codes.

Description

technical field [0001] The invention belongs to the field of digital integrated circuits and cryptography, and in particular relates to a method for judging the affine equivalence of two Boolean functions of arbitrary variables. The judging method points out the necessary conditions for the affine equivalence of two Boolean functions ; and when the number of variables is small, the affine equivalence class of the Boolean function represents the selection method of the element. Background technique [0002] Boolean functions have important applications in many fields of science and technology. Affine equivalence is a basic equivalence relation of Boolean functions, which is widely used in fields such as circuit design and cryptography. The application of the affine equivalence classification of Boolean functions in circuit design is mainly reflected in the design of combinational logic circuits and the design of FPGA (the abbreviation of Filed Programmable Gate Array, that i...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/00
Inventor 杨国武张艳牛伟纳吕凤毛徐栋王双宝冯丽丽
Owner UNIV OF ELECTRONICS SCI & TECH OF CHINA
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com