Implementation method for rapid scalar multiplication algorithm in elliptic curve cryptosystem
An elliptic curve cryptography and implementation method technology, applied in the field of fast point multiplication algorithm, can solve the problems of many calculation cycles, slow calculation speed, low calculation speed, etc., achieve high calculation speed, reduce the number of calculation cycles, and speed up the calculation speed Effect
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0019] The present invention will be further described below in conjunction with the accompanying drawings, but the protection scope of the present invention is not limited to the following description.
[0020] Such as figure 1 , figure 2 As shown, the implementation method of the fast point product algorithm in the elliptic curve cryptosystem, it at least includes the following steps of the point product algorithm with the minimum Hamming weight signed binary code from left to right:
[0021] Assume defined in a finite prime field superior, for any point, is any integer, in the algorithm for binary code;
[0022] enter: ;
[0023] output: ;
[0024] A. make , , ;
[0025] B. right decremented to ,implement:
[0026] a. make ;
[0027] b. , , ;
[0028] c. if ,make ;
[0029] C. return .
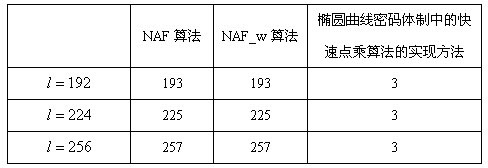
[0030] From the perspective of the storage space required by the algorithm, comparing the storage space of several dot product algorit...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com