Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Nonlinear sensor compensation method based on free node recursion B-spline

A nonlinear compensation and sensor technology, applied in the field of sensors, can solve problems such as large amount of calculation, achieve the effect of small amount of calculation, improve accuracy, and reduce workload

Inactive Publication Date: 2011-10-19
HARBIN INST OF TECH
View PDF5 Cites 5 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to provide a sensor nonlinear compensation method based on free node recursive B-splines in order to solve the problem of large amount of calculation based on the inverse model nonlinear compensation method adopted by the existing sensor

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Nonlinear sensor compensation method based on free node recursion B-spline
  • Nonlinear sensor compensation method based on free node recursion B-spline
  • Nonlinear sensor compensation method based on free node recursion B-spline

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

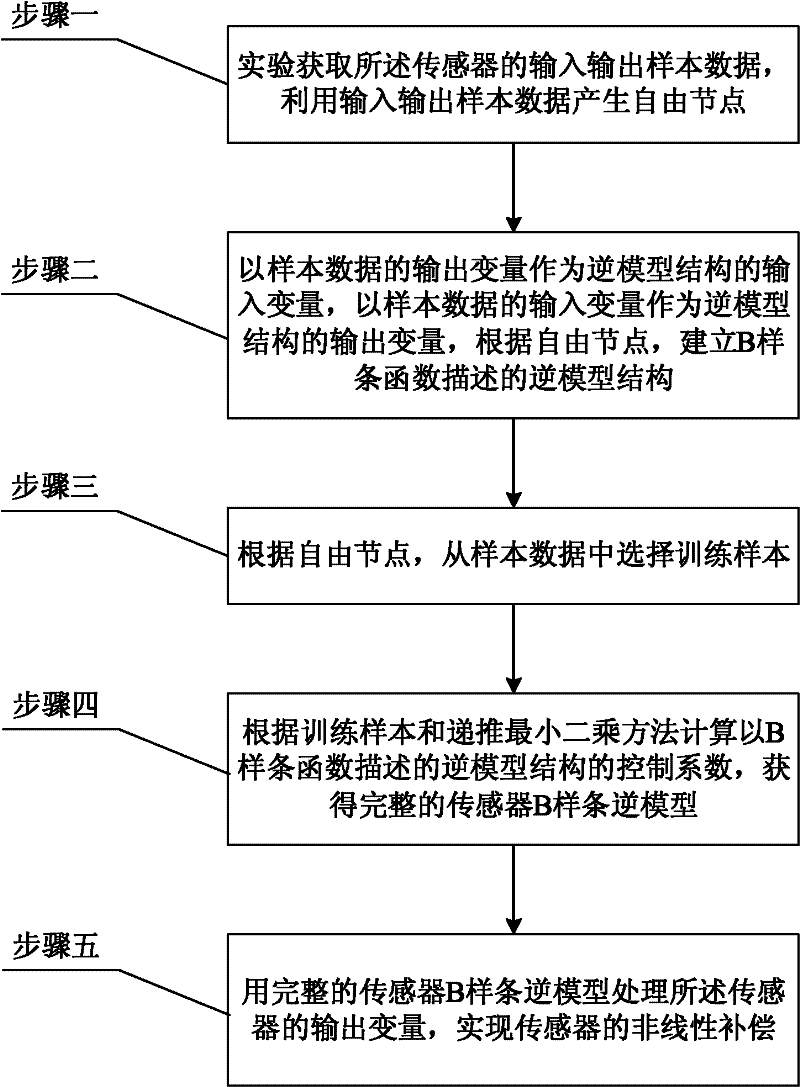
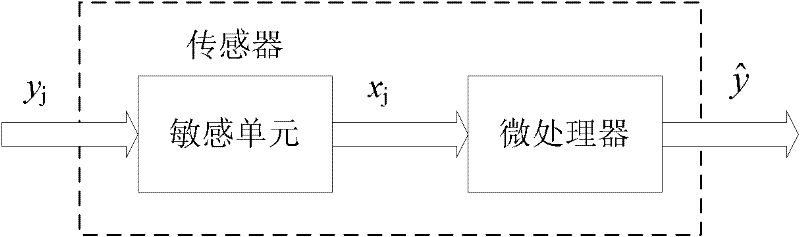
[0019] Specific implementation mode one: the following combination figure 1 and figure 2 Describe this implementation mode, this implementation mode comprises the following steps:

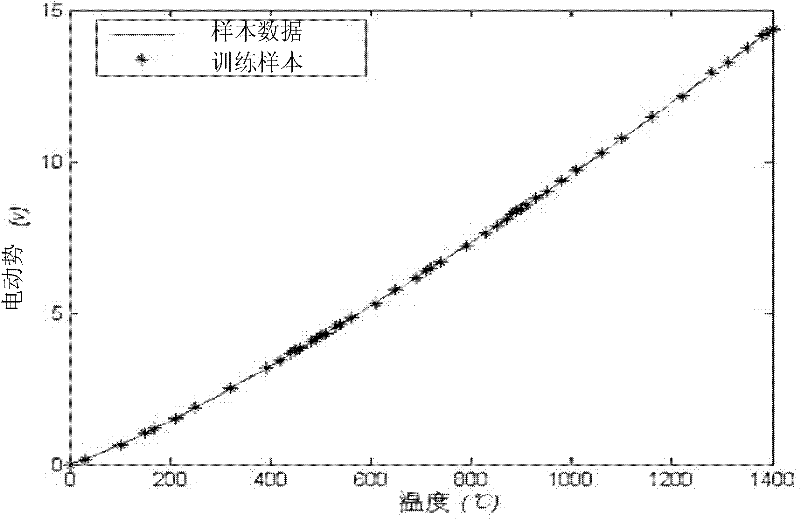
[0020] Step 1: Experimentally obtain the input and output sample data of the sensor, and use the input and output sample data to generate free nodes;

[0021] Step 2: using the output variable of the sample data as the input variable of the inverse model structure, taking the input variable of the sample data as the output variable of the inverse model structure, and establishing the inverse model structure described by the B-spline function according to the free nodes;

[0022] Step 3: Select training samples from sample data according to free nodes;

[0023] Step 4: Calculate the control coefficient of the inverse model structure described by the B-spline function according to the training samples and the recursive least squares method, and obtain a complete sensor B-spline inverse model;

[...

specific Embodiment approach 2

[0027] Embodiment 2: This embodiment is a further description of Embodiment 1. In this embodiment, the method of using input and output sample data to generate free nodes is:

[0028] Step 11: The expression of the node vector t is:

[0029] The initial node vector is t 0 :

[0030] t 0 = ( t - k + 1 0 , . . . , t - 1 0 , a = t 0 0 , t 1 0 = b , t 2 0 , . . . , ...

specific Embodiment approach 3

[0044]Specific embodiment three: this embodiment is a further description to embodiment two, and in step two, according to free nodes, the method for setting up the inverse model structure described by B-spline function is:

[0045] Establish B-spline basis functions according to the free nodes generated in step 1

[0046]

[0047] According to the B-spline basis function Obtain the inverse model structure described by the B-spline function as:

[0048] y j = Σ i = - k + 1 N c i B i , t k ( x j ) + e j = Σ i = - ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a nonlinear sensor compensation method based on a free node recursion B-spline, belonging to the technical field of sensors. The method solves the problem that the calculation quantity is large as the existing sensor adopts a nonlinear compensation method based on an inverse model. The method comprises the following steps of obtaining input and output sample data of a sensor through experiments; generating free nodes by the input and output sample data; taking output variables of the sample data as input variables of an inverse model structure; taking the input variables of the sample data as the output variables of the inverse model structure; establishing an inverse model structure described by a B-spline function according to the free nodes; selecting training samples from sample data according to the free nodes; calculating control coefficients of the inverse model structure described by the B-sample function according to the training samples and a recursiveleast square algorithm(RLS) so as to obtain the complete B-spline inverse model of the sensor; and processing the output variables of the sensor by the complete B-spline inverse model of the sensor to realize nonlinear compensation of the sensor. The method is applicable to the nonlinear compensation of the sensor.

Description

technical field [0001] The invention relates to a sensor nonlinear compensation method based on free node recursive B-splines, belonging to the technical field of sensors. Background technique [0002] The nonlinear compensation technology is an indispensable part of the sensor. Commonly used sensor signal compensation algorithms include look-up table method, genetic algorithm, support vector machine and neural network method. Among them, the look-up table method is the simplest and most traditional method. Its accuracy depends entirely on the interval of data in the table, and it requires high storage space. Several other methods are nonlinear compensation methods based on the inverse model. Although these methods can achieve high modeling accuracy, they do not consider the complexity of modeling enough, and the calculation of model parameters requires a lot of system resources; at the same time, these methods do not consider the calibration optimization problem for a larg...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01D3/028
Inventor 魏国王昕孙金玮李清连
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com