Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for controlling rigid spacecraft for target attitude tracking

A technology of target attitude and control method, which is applied in the observation of astronauts, guidance devices of astronauts, and astronaut equipment, etc., can solve the problem of inability to eliminate the inherent vibration of sliding mode variable structure, and achieves the solution of inherent vibration, Guaranteed stability and improved control accuracy

Inactive Publication Date: 2010-05-19
HARBIN INST OF TECH
View PDF0 Cites 58 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The purpose of the present invention is to solve the problem that the inherent vibration of the sliding mode variable structure cannot be eliminated in the existing control method when the attitude tracking spacecraft is running in low orbit in outer space, and a rigid spacecraft for target attitude tracking is provided control method

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for controlling rigid spacecraft for target attitude tracking
  • Method for controlling rigid spacecraft for target attitude tracking
  • Method for controlling rigid spacecraft for target attitude tracking

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

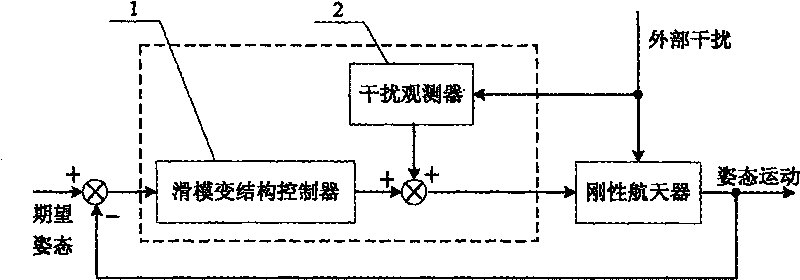
[0012] Specific implementation mode one: the following combination figure 1 and figure 2 Describe this embodiment, this embodiment realizes based on sliding mode variable structure controller 1 and disturbance observer 2, and it comprises the following steps:

[0013] Step 1: Establish the dynamics and kinematics model of the rigid spacecraft;

[0014] Step 2: Set the attitude tracking error of the rigid spacecraft and the expected attitude parameters corresponding to the attitude tracking error, and then combine the attitude tracking error and the expected attitude parameters with the dynamics and kinematics model established in step 1 to establish A mathematical model for attitude tracking of rigid spacecraft;

[0015] Step 3: using the control algorithm of the sliding mode variable structure controller 1 to adjust the control law of the mathematical model used for attitude tracking established in step 2, and modify the control law in combination with the observation resu...

specific Embodiment approach 2

[0017] Specific embodiment two: this embodiment is a further description of step one in embodiment one: the dynamic model of the rigid spacecraft in step one is:

[0018] J ω · + ω × ( Jω ) + u = d ,

[0019] The dynamic model of a rigid spacecraft is:

[0020] q · = 1 2 Ω ( ω ) · q ,

[0021] In the formula, J is the moment of inertia matrix of the spacecraft, ω is the angular velocity vector of the spacecraft relative to the inertial coordinate system in the body coordinate system, u is the control law, and d is the external disturbance moment; q is the attitude quaternion of the rigid spacecraft, and satisfy the constraints Ω(ω) is the input matrix containing...

specific Embodiment approach 3

[0022] Specific Embodiment Three: This embodiment is a further description of Step 2 in Embodiment 1: the attitude tracking error in Step 2 is set to q e and ω e , the desired attitude parameter is set to q d and ω d , define the quaternion multiplication, then the formula for establishing the relationship between the attitude tracking error and the expected attitude parameters is:

[0023] q e = q d - 1 ⊗ q ,

[0024] ω e =ω-A×ω d ,

[0025] In the formula Represents the quaternion multiplication, A represents the transformation matrix from the orbital coordinate system of the spacecraft to the body coordinate system, combines the formula and the dynamics and kinematics model established between the attitude tracking error and the expected attitude parameters, and establishes a method for attitude The mathematical...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a method for controlling a rigid spacecraft for target attitude tracking, and belongs to the technical field of the high-precision and high-stability attitude tracking control of spacecrafts. The method solves the problem that when the attitude tracking spacecraft runs in a low orbit in outer space, the conventional control method cannot eliminate the inherent flutter of a sliding mode variable structure. The method comprises the following steps: 1, establishing a kinetic model and a kinematic model of the rigid spacecraft; 2, setting an attitude tracking error and anexpected attitude parameter of the rigid spacecraft, and combining the attitude tracking error and the expectation attitude parameter with the kinetic model and the kinematic model to establish a mathematical model for the attitude tracking; 3, adopting a control algorithm of a sliding mode variable structure controller to adjust a control law of the mathematical model which is established in thestep 2 and is used for the attitude tracking, and simultaneously combining an observation result of a disturbance observer to modify the control law; and 4, controlling the rigid spacecraft by using the modified control law obtained in the step 3 to realize the attitude tracking. The method is suitable for the attitude tracking of targets running in the outer space.

Description

technical field [0001] The invention relates to a control method for a rigid spacecraft used for target attitude tracking, and belongs to the technical field of high-precision and high-stability attitude tracking control of spacecraft. Background technique [0002] Attitude tracking technology has important application value in many fields such as spacecraft formation flight, ground monitoring and imaging. The control method to realize spacecraft attitude tracking is the core technology, and there have been many researches and applications at home and abroad. For example: traditional PID control, fuzzy control and adaptive control, etc., but these methods have certain limitations. There are relatively large environmental moments in the middle and low orbits of outer space spacecraft, and these environmental moments will seriously affect the attitude motion of the spacecraft. Therefore, the control method of attitude tracking of spacecraft in low-orbit orbit in outer space ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): B64G3/00B64G1/24
Inventor 孙兆伟邬树楠苗赢吴限德陈长春
Owner HARBIN INST OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com