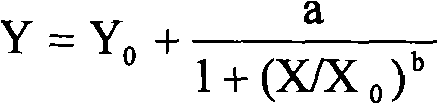Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for forecasting rhizoma atractylodis growth by four-parameter logistic equation

A technique of logistic equation and logistic regression, applied in the field of agricultural engineering

Inactive Publication Date: 2010-02-10
JIANGSU UNIV
View PDF0 Cites 9 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The present invention is exactly a kind of method that utilizes four parameter logistic equations to predict the growth of Atractylodes atractylodes, and this has not been reported at home and abroad

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for forecasting rhizoma atractylodis growth by four-parameter logistic equation
  • Method for forecasting rhizoma atractylodis growth by four-parameter logistic equation
  • Method for forecasting rhizoma atractylodis growth by four-parameter logistic equation

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0014] Example 1 Prediction of notched leaf type Atractylodes atractylodes

[0015] Obtain the maximum thickness data of the main stem of the notched leaf-type Atractylodes atractylodis over time in the middle of the hill, and use these data to construct a four-parameter logistic equation, as shown in Table 1.

[0016] The instant observation value (0.80mm, the upper part of the hill; 0.70mm, the bottom of the hill) of the maximum thickness of the main stem of the notched leaf shape of the to-be-predicted hill (0.80mm, the upper part of the hill; 0.70mm, the bottom of the hill) is brought into the above four-parameter logistic equation as Y, Calculate the number of days after the start of growth and denote it as Xs. The Xs at the upper part of the hill is 14.01 days, and the Xs at the bottom of the hill is 12.74 days. Add the predicted number of days to Xs to find the predicted growth days, denoted as Xa, take Xa as the X value of the above equation, bring it into the above f...

Embodiment 2

[0025] Example 2 Prediction of Atractylodes ovaliforme

[0026] Obtain the maximum thickness data of the main stem of Atractylodes ovalifolia over time in the middle of the hill, and use these data to construct a four-parameter logistic equation, as shown in Table 3.

[0027] The instant observed value of the maximum thickness of the main stem of the ovale-shaped Atractylodes atractylodes at the top and bottom of the hill to be predicted (0.45mm, the top of the hill; 0.63mm, the bottom of the hill) is brought into the above four-parameter logistic equation as Y, Calculate the number of days after the start of growth and denote it as Xs. The Xs at the upper part of the hill is 15.19 days, and the Xs at the bottom of the hill is 18.10 days. Add the predicted number of days to Xs to find the predicted growth days, denoted as Xa, take Xa as the X value of the above equation, bring it into the above four-parameter logistic equation, and predict the main stem at this time maximum ...

Embodiment 3

[0037] Example 3 Prediction of Long-lanceolate-leafed Atractylodes atractylodes

[0038] Obtain the maximum thickness data of the main stem of the long-lanceolate-leafed Atractylodes lanceolata in the middle of the hill over time, and use these data to construct a four-parameter logistic equation, as shown in Table 5.

[0039] Take the real-time observation value of the maximum thickness of the main stem of the long-lanceolate-shaped Atractylodes lanceolata at the top and bottom of the hill to be predicted (0.66mm, at the top of the hill; 0.68mm, at the bottom of the hill) as Y into the above four-parameter logistic equation In , the number of days after the start of growth was calculated and recorded as Xs. The Xs of the upper part of the hill is 16.88 days, and the Xs of the bottom of the hill is 17.29 days. Add the predicted number of days to Xs to find the predicted growth days, denoted as Xa, take Xa as the X value of the above equation, bring it into the above four-para...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for forecasting rhizoma atractylodis growth by a four-parameter logistic equation, which relates to the field of agricultural engineering. The regression analysis is executed by biomass (Y) of measured growth indexes and data of measured growth time (X) for computing reasonable regression coefficients: a, Y0, X0 and b; a four-parameter logistic regression equationis established as follows: Y=Y0+a / (1+(x / x0)), wherein in the four-parameter logistic regression equation, Y is the measured biomass, Y0 is the initial biomass of entering a logarithmic growth phase, a is the upper limit of the biomass along with time, X0 is the number of days when reaching half of the logarithmic growth phase, X is the measured growth time and b is a coefficient, i.e. a constant. The method can be used for forecasting the growth of all kinds of rhizoma atractylodis and providing guidance for fertilizing all kinds of rhizoma atractylodis, selecting picking and harvesting time and evaluating the yield.

Description

technical field [0001] The invention relates to the field of agricultural engineering, in particular to a method for predicting the growth of Atractylodes atractylodes by four-parameter logistic equation. Background technique [0002] The logistic equation, which can express the relationship of plant biomass with time, was used to characterize plant growth. Two-parameter or three-parameter logistic equations have been successfully used to fit plant stem thickening, plant height increase, and leaf area expansion, but their use to predict plant growth has not been reported. The four-parameter logistic equation not only has more advantages in fitting the plant growth, but also is suitable for predicting the dynamic growth of the plant due to the increase of the information of the initial biomass entering the logarithmic growth phase. [0003] Atractylodes Lancea (Thunb.) DC. is a perennial herb of Compositae, and its dried rhizome can be used as medicine. "Chinese Pharmacopoe...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): A01G1/00A01G7/00
Inventor 吴沿友李萍萍桑小花杨晓勇毛罕平赵玉国
Owner JIANGSU UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com