Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Underwater target positioning method based on probability graph model

A probabilistic graphical model and positioning method technology, applied in positioning, measuring devices, instruments, etc., can solve the problems of low information update rate and inability to obtain high precision.

Active Publication Date: 2021-04-23
哈尔滨工程大学青岛船舶科技有限公司
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0012] The purpose of the present invention is to solve the problem that the existing technology cannot obtain high-precision underwater target positions when the beacons are sparse and the information update rate is low, and provides an underwater target positioning method based on a probability graph model

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Underwater target positioning method based on probability graph model
  • Underwater target positioning method based on probability graph model
  • Underwater target positioning method based on probability graph model

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0090] Specific embodiment one: a kind of underwater target localization method based on the probabilistic graph model described in this embodiment, this localization method comprises:

[0091] S1. Under sparse conditions, obtain all the distance data and speed data of a single target within a period of time, and use the distance data and speed data as local variables respectively, and use the factor graph to represent the global joint probability distribution of each local variable to obtain a global function;

[0092] S2. Complement and calculate the global function, solve the marginal function, and obtain the estimated position of the target at each moment;

[0093] S3. The sum-product algorithm is used to calculate the marginal function, and the marginal probability function of each local variable of the joint distribution is solved to obtain target estimation results at different moments.

specific Embodiment approach 2

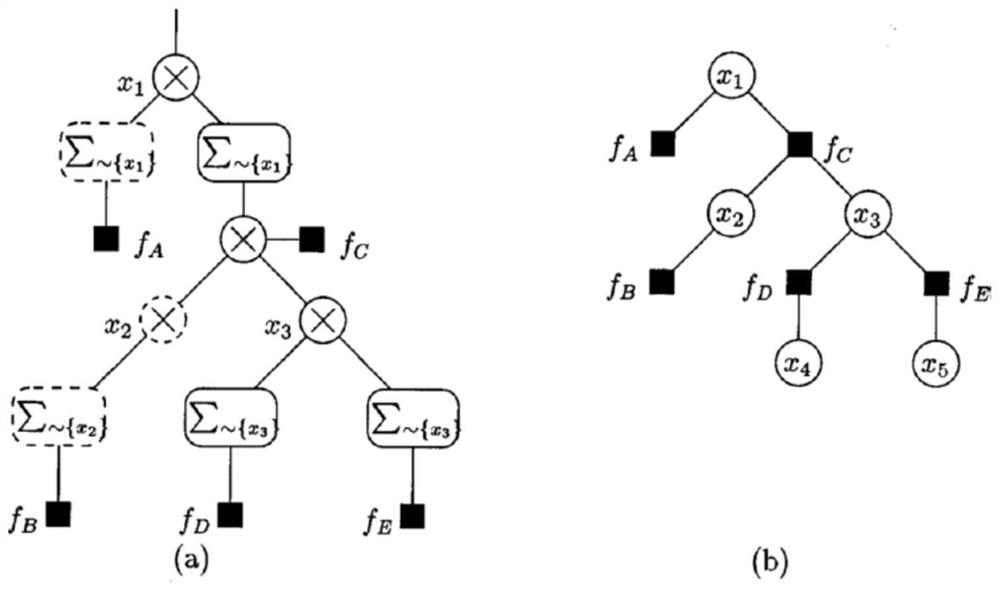
[0094] Specific implementation mode two: the following combination figure 1 Illustrate this embodiment, this embodiment will further illustrate specific embodiment 1, if the global function described in S1 includes five variables, then the global function is expressed as:

[0095] g(x 1 ,x 2 ,x 3 ,x 4 ,x 5 ) = f A (x 1 ) f B (x 2 ) f C (x 1 ,x 2 ,x 3 ) f D (x 3 ,x 4 ) f E (x 3 ,x 5 );

[0096] where: x 1 、x 2 、x 3 、x 4 and x 5 represent five local variables respectively, and the obtained five local functions are f A , f B , f C , f D and f E ;

[0097] The subvariable discrete address set is J={A, B, C, D, E};

[0098] The local function sub-variable sets are: X A ={x 1}, X B ={x 2}, X C ={x 1 ,x 2 ,x 3}, X D ={x 3 ,x 4}, X E ={x 3 ,x 5}.

[0099] In this embodiment, figure 1 In the represented factor graph, there are five variable nodes (circles) corresponding to five variables, five function nodes (squares) corresponding to five ...

specific Embodiment approach 3

[0100] Specific implementation mode three: this implementation mode further explains specific implementation mode two, and the method for calculating and solving the edge function of the global function described in S2 includes:

[0101] Let A i represents the global variable x i , all value sets of i=1,2,3,4,5, when there is a is A i A subset of , then gi (a) represents the global function g(x 1 ,x 2 ,x 3 ,x 4 ,x 5 ) meets x i = sum of all combinations of a;

[0102] The global function g(x 1 ,x 2 ,x 3 ,x 4 ,x 5 ) for variable x i Complementary sum to obtain the marginal function g of the global function i (x i ):

[0103]

[0104] In this embodiment, for variables that do not contain x i The process of summing the remaining variables of is called complement summation. For example: Suppose a global function h consists of three variables, for one of the variables y 2 Find the edge function, you can get:

[0105]

[0106] In this embodiment, according ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an underwater target positioning method based on a probability graph model, belongs to the technical field of underwater positioning, and aims to solve the problem that a high-precision underwater target position cannot be obtained when beacons are sparse and the information updating rate is low in the prior art. The method comprises the following steps: obtaining all distance data and speed data of a single target in a period of time under a sparse condition, taking the distance data and the speed data as local variables respectively, and representing global joint probability distribution of each local variable by adopting a factor graph to obtain a global function; carrying out complementation and calculation on the global function, solving an edge function, and obtaining a position estimation value of the target at each moment; and calculating an edge function by adopting a sum product algorithm, solving an edge probability function of each local variable in joint distribution, and obtaining target estimation results at different moments. The method is used for accurately positioning the underwater target.

Description

technical field [0001] The invention relates to an underwater target positioning method based on a probability graph model, belonging to the technical field of underwater positioning. Background technique [0002] With the increasing attention of human beings to marine resources, underwater targets such as underwater vehicles and underwater weapons are developing rapidly, and it is of great significance to locate and track underwater targets. However, due to the complex underwater environment, the noise has a great influence on the positioning results of underwater targets, and the simple calculation of equations cannot obtain the definite position, or the calculated position deviates greatly from the actual position. Therefore, for different underwater conditions, Need to choose a different positioning solution method. Positioning algorithms usually include: intersection method, dead reckoning method and collaborative method. [0003] (1) The intersection method is to sel...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G01S5/02
CPCY02D30/70
Inventor 孙大军张居成韩云峰郑翠娥徐敏
Owner 哈尔滨工程大学青岛船舶科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com