J2 perturbation Lambert problem solving method based on deep neural network and targeting algorithm
A deep neural network and problem solving technology, applied in the field of J2 perturbation Lambert problem solving, can solve problems such as insufficient convergence stability, poor solving effect, low computational efficiency, etc., to reduce the number of iterations and computational time, ensure stability, The effect of maintaining computational efficiency
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
example
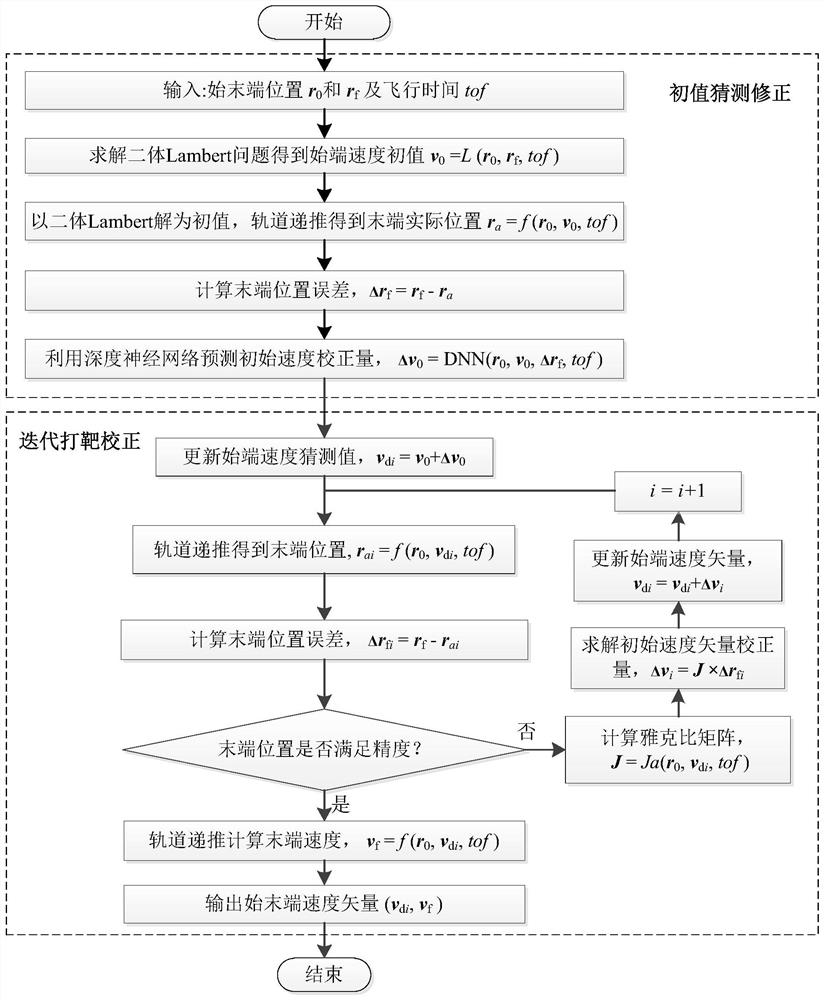
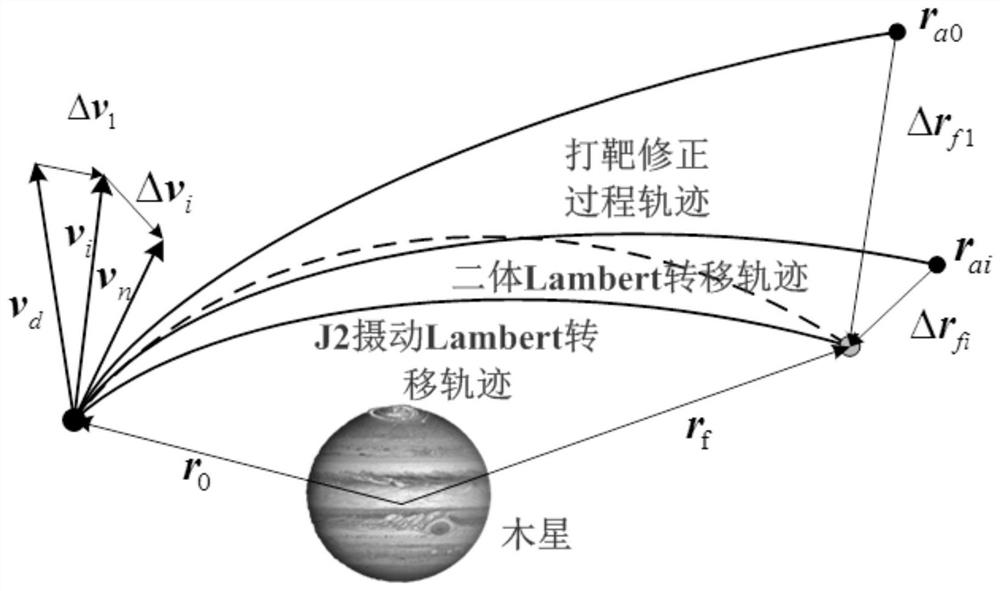
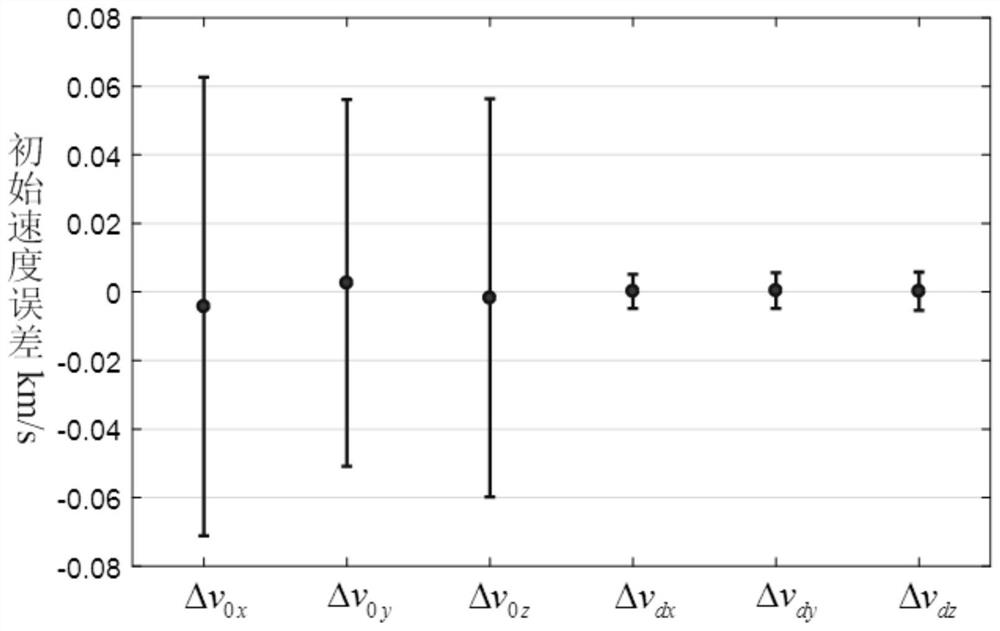
[0071] Example of the method of the invention: combining Figure 3a , Figure 3b , Figure 4 with Figure 5 Illustrate the example verification of the present invention, set following calculation condition and technical parameter:
[0072] (1) With Jupiter as the central celestial body, the average equatorial radius of Jupiter is R J =71492km, the gravitational constant of Jupiter is μ J =126686543.922km 3 / s 2 , the J2 perturbation term coefficient is J2=0.01475.
[0073] (2) The parameter value range of the random sample is set as follows:
[0074]
[0075] Among them, r is the initial orbital radius, e is the initial orbital eccentricity, i is the initial orbital inclination, Ω is the right ascension of the initial ascending node, ω is the initial argument of perigee, u is the initial true anomaly, tof is the time of flight, T is the orbital period of the initial orbit, (a is the semi-major axis of the initial orbit).
[0076] (3) The target shooting accuracy ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com