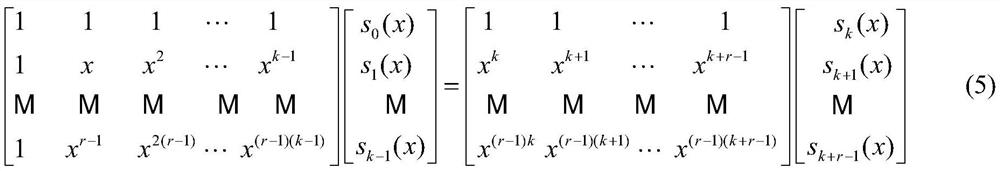Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Universal EBR encoding method and decoding method thereof

A technology of encoding method and decoding method, which is applied in the field of EBR encoding method and its decoding method, can solve the problems of high computational complexity of decoding method, low decoding efficiency, limited selection of EBR encoding parameters, etc., and achieve low decoding complexity and high decoding efficiency. The effect of high efficiency and low complexity

Active Publication Date: 2020-11-24
DONGGUAN UNIV OF TECH
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0015] The present invention provides a general EBR encoding method and its decoding method in order to solve the problems that the selection of existing EBR encoding parameters is limited, and its decoding method has high computational complexity and low decoding efficiency.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Universal EBR encoding method and decoding method thereof
  • Universal EBR encoding method and decoding method thereof
  • Universal EBR encoding method and decoding method thereof

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

[0059] Specific embodiment one: a kind of general EBR encoding method that this embodiment provides, specifically comprises the following steps:

[0060] Step 1, for the original k(p-1)τ information bits, define a pτ×(k+r) matrix, where τ is a positive integer, p is a prime number, k=p-r; 1≤ri,j Represents the elements of the i-th row and j-th column of the pτ×(k+r) matrix, i=0,1,...,pτ-1; j=0,1,...,k+r- 1; Given k(p-1)τ information bits s i,j , that is, the original k(p-1)τ information bits are sequentially used by s i,j To represent, take i=0,1,...,(p-1)τ-1 at this time; j=0,1,...,k-1;

[0061] Step 2, calculate the τ parity bits s in column j according to formula (2) (p-1)τ,j ,s (p-1)τ+1,j ,K,s pτ-1,j :

[0062]

[0063] where μ=0,1,...,τ-1; l=0,1,...,p-2;

[0064] Step 3. In order to determine other parity digits, set pτ in column j to s 0,j ,s 1,j ,K,s pτ-1,j Expressed as a quotient ring GF(2)[x]mod(1+x pτ ) in a polynomial s j (x)=s 0,j +s 1,j x+s 2,j x2...

specific Embodiment approach 2

[0117] Specific embodiment two: a kind of universal EBR coded decoding method that this embodiment provides, described decoding method is in ring R pτ Based on the LU decomposition algorithm to solve the Vandermonde linear equation (LU decomposition is essentially an expression of the Gaussian elimination method, which essentially transforms the matrix into an upper triangular matrix through elementary row transformation), it can effectively solve the equations such as Formula (6), specifically includes the following process:

[0118] A. In the ring R pτ on 1+x b The division calculation of

[0119] Theorem 4: b is a positive integer, 1≤bb )g(x)=f(x)mod(1+x pτ The coefficient g of g(x) in ) j for:

[0120]

[0121] where j=0,1,...,n-1;

[0122] Other coefficients can be obtained iteratively: g bl+j = f bl+j +g b(l-1)+j ,in

[0123] Proof: (1+x b )g(x)=f(x), wherein, 1≤b

[0124] Solve for g(x), i.e. find 1+x b In the ring GF(2)[x] / 1+x pτ the ...

Embodiment 1

[0142] When r=3, a 3×3 Vandermonde matrix;

[0143] phalanx

[0144]

[0145] Calculate the complexity as follows:

[0146] Solving Linear Equations uL r (1) L r (2) …L r (r-1) u r (r-1) u r (r-2) …U r (1) =v can be carried out by the following steps: input: positive integer r, prime number p, integer a 1 ,a 2 ,...,a r ;v=(v 1 (x),...,v r (x))∈C pτ ;Output: u=(u 1 (x),...,u r (x))∈C pτ , and satisfy uV r×r (a)=vmod(1+x pτ );

[0147] Requirement: for all 1≤i 1 ≤ i 2 ≤r, with M pτ (x) is mutually prime in GF(2)[x];

[0148]

[0149]

[0150] Steps 2-4 require r(r-1) / 2 additions and r(r-1) / 2 multiplications, steps 5-9 require r(r-1) / 2 additions and r(r-1) / 2 divisions (factor ).

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a universal EBR encoding method and a decoding method thereof, relates to an EBR encoding method and a decoding method thereof, and belongs to the technical field of distributedstorage systems. The universal EBR encoding method comprises the following step of encoding original k (p-1) tau information bits to generate a ptau * (k + r) matrix; the universal decoding method for EBR coding is based on an LU decomposition algorithm of a Van der Monte Carlo matrix. The invention aims to solve the problems that the selection of existing EBR coding parameters is limited, and adecoding method of the EBR coding parameters is high in calculation complexity and relatively low in decoding efficiency. The methods can be applied to a distributed storage system.

Description

technical field [0001] The invention relates to an EBR encoding method and a decoding method thereof, and belongs to the technical field of distributed storage systems. Background technique [0002] Modern distributed storage systems use erasure coding to maintain data availability and reliability. Redundancy is necessary to provide high data reliability, and the two main methods of introducing redundancy are duplicating the original data and employing erasure coding. Compared with replication technology, erasure coding can provide higher data reliability and lower storage overhead. Using erasure codes, the data file is divided into k information blocks of the same size for encoding calculation, and r parity blocks are obtained. Information bits and parity bits are stored in the storage system at the same time to achieve high data reliability. [0003] Array codes composed of m×n arrays have been widely used in storage systems, such as RAID (Redundant Array of Independent...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L29/08H04L1/00
CPCH04L67/1097H04L1/0056
Inventor 侯韩旭吴优韩永祥李柏晴韩国军
Owner DONGGUAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com