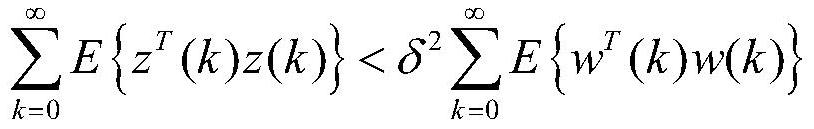Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

An Intelligent Control Method of Adjacent State Bias for Jump System with Unknown Transition Probability

An intelligent control and transition system technology, applied in the field of engineering systems, can solve the problem that the transition probability information cannot be known in advance

Active Publication Date: 2021-04-02
JIANGNAN UNIV
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, in the application process, the transition probability information of most practical systems cannot be known in advance, which makes the traditional control methods described by linear matrix inequalities or Riccati equations have their limitations

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • An Intelligent Control Method of Adjacent State Bias for Jump System with Unknown Transition Probability
  • An Intelligent Control Method of Adjacent State Bias for Jump System with Unknown Transition Probability
  • An Intelligent Control Method of Adjacent State Bias for Jump System with Unknown Transition Probability

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0055] This embodiment provides an intelligent control method for adjacent-state deviation using an unknown transition probability jump system for the control problem of the DC motor jump circuit system in engineering technology. The method includes:

[0056] Step 1: Establish a discrete Markov jump system model of the DC motor jump circuit system. First, the motor dynamics of the DC jump circuit are described as:

[0057]

[0058]

[0059] Among them, r(t)=1, 2, 3 respectively represent the working states of the motor in three power modes: normal power, low power, and medium power. The system has different parameters in different working modes. t is the continuous time, u(t) is the total input voltage, i is the motor current, v(t) is the angular velocity of the motor; K m is the motor load constant, K e is the counter electromotive force constant, K d is the damping constant, R m is the total resistance of the circuit connection, L is the inductance; J is the mecha...

Embodiment 2

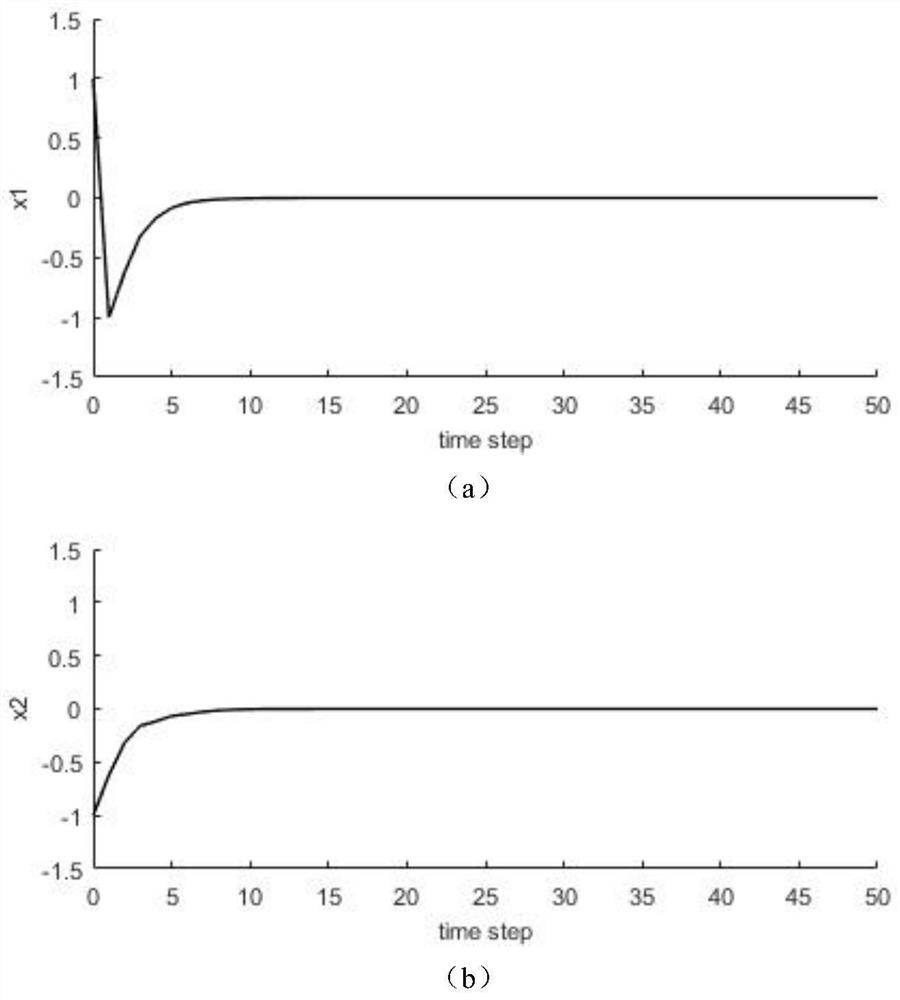
[0099] In this embodiment, aiming at the DC motor jump circuit, an intelligent control method for adjacent state deviation of an unknown transition probability jump system is provided for simulation experiment verification. In order to verify the effectiveness of the proposed method, the parameters of the discrete Markov jump system are described as follows :

[0100]

[0101] B 1 =B 2 =B 3 =(0 1) T ,

[0102]

[0103] D. 1 =D 2 =D 3 =(0 0 1) T , G 1 =G 2 =G 3 =(0 0.1) T .

[0104] Without loss of generality, the transition probability matrix is ​​selected to obey the Gaussian random distribution, and the randomness is described by the following Gaussian probability density matrix:

[0105]

[0106] Among them, n(μ,σ) represents the Gaussian transition probability density function, μ is the mean, and σ is the variance.

[0107] Select the modal trajectory length K=20, the number of trajectories T=500, the weight rate λ=0.1, and the anti-interference pe...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an adjacent state deviation intelligent control method of an unknown transition probability hopping system and belongs to the field of engineering systems. The method comprisesthe following steps of for a Markov jump system, describing uncertainty of the modal transition probability of the Markov jump system by an unknown distribution, and establishing an anti-interferencecontrol problem model; secondly, constructing an updating form of a modal dependence value function; obtaining a modal track according to the input control strategy, and calculating adjacent state deviation so as to update the value function till convergence; and finally, optimizing a control strategy according to the value function, and repeating the process till the control strategy converges,thereby obtaining a controller which can enable a system closed loop to be stable and meet the specified interference suppression performance. The Markov jump system control method solves a control problem of the Markov jump system under the condition that the transition probability is completely unknown, and has very important practical significance.

Description

technical field [0001] The invention relates to an intelligent control method for an adjacent state deviation of an unknown transition probability jump system, which belongs to the field of engineering systems. Background technique [0002] For several years, the control problem of Markov (Markov) jump system has been one of the research hotspots in the field of control. As a typical multimodal stochastic system, the Markov jump system can be used to simulate a dynamic system with mutation characteristics, generally a dynamic system with random mutation characteristics due to external environment disturbance or changes in internal structure and parameters, such as Industrial systems, fault-tolerant control systems, network control systems, etc. Transition probability, as a key factor of the system, describes the random dynamic characteristics of mode hopping. [0003] Under the condition that the transition probability is known or partially known, the research on Markov ju...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G05B13/04
CPCG05B13/042
Inventor 栾小丽陈垚钢赵顺毅刘飞
Owner JIANGNAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com