Smooth particle dynamics modeling method for solid structure

Abstract

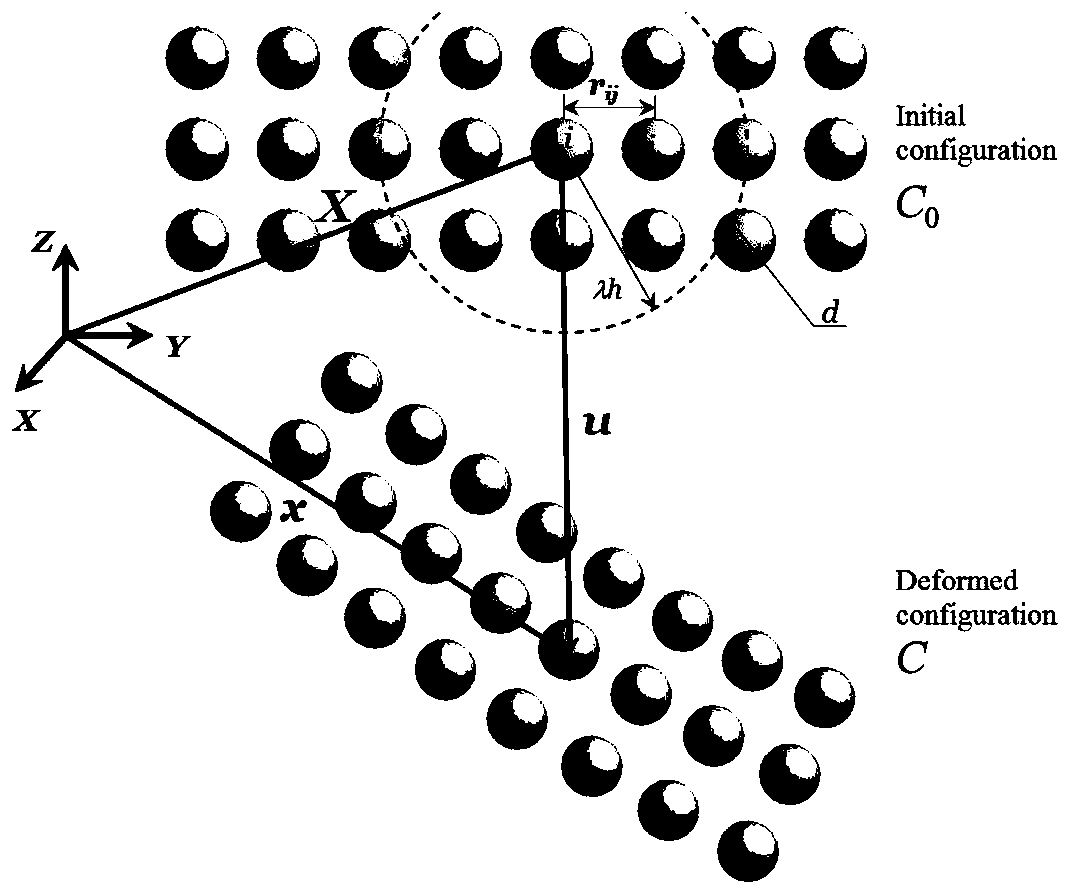
The invention relates to the field of materials, and provides a solid structure smooth particle dynamics modeling method. The method comprises the steps: discretizing a planar solid structure into SPHparticles, wherein each particle carries at least one kind of same physical information; deformation occurs at a spatial point xi, and calculating a correction mode of a smooth function derivative atthe spatial point xi; then calculating the deformation of the spatial point xi; and finally, in a deformation state, calculating the deformation gradient at the spatial point xi. According to the invention, a smooth function correction method and a complete Lagrange SPH method are combined to obtain the correction mode of the smooth function derivative as an integral kernel, so the first-order completeness of the numerical method is ensured, the boundary calculation accuracy is improved, the stretching instability phenomenon is eliminated, the calculation time is greatly saved, and the boundary defects and instability of the traditional SPH are overcome.

Description

technical field [0001] The invention relates to the technical field of materials, and more specifically relates to a dynamic modeling method of solid structure smooth particles. Background technique [0002] Composite materials are structural materials with the highest specific strength currently available, and have the advantages of excellent energy absorption performance, high fatigue life, and low manufacturing cost. Smoothed Particle Hydrodynamics (SPH) integrates discrete particle physical information through the "smooth function" integral kernel, and completes the numerical modeling of laminate impact damage, which overcomes the shortcomings of traditional finite element methods such as large amount of calculation and limited simulation accuracy . [0003] The core of the SPH method is the interpolation theory. It does not need to use any grid when calculating the spatial derivative. Instead, an integral kernel called "smooth function" is used to approximate the "smoo...

AI Technical Summary

Problems solved by technology

However, after discretizing the solution domain into particles, the integral form is converted into a weighted sum form, and the number of particle points at the boundary is too small, and the smooth function is truncated by the boundary, which will make the SPH approximate function and its derivatives not complete enough, resulting in poor SPH accuracy. Boundary defects are very prominent

In addition, when the traditional SPH method solves the problem of solid mechanics, there will be unstable motion, resulting in the non-physical aggregation of the particles, or even fracture, which is called tensile instability.

Images