Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Dynamic Modeling Method for Smooth Particles with Solid Structure

A technology of dynamic modeling and solid structure, applied in the field of materials, it can solve the problems of insufficient completeness of the derivative of the SPH approximate function, poor SPH accuracy, unstable motion, etc. Stability phenomenon and the effect of saving computing time

Active Publication Date: 2022-04-01
SHANDONG UNIV
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, after discretizing the solution domain into particles, the integral form is converted into a weighted sum form, and the number of particle points at the boundary is too small, and the smooth function is truncated by the boundary, which will make the SPH approximate function and its derivatives not complete enough, resulting in poor SPH accuracy. Boundary defects are very prominent
In addition, when the traditional SPH method solves the problem of solid mechanics, there will be unstable motion, resulting in the non-physical aggregation of the particles, or even fracture, which is called tensile instability.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Dynamic Modeling Method for Smooth Particles with Solid Structure
  • A Dynamic Modeling Method for Smooth Particles with Solid Structure
  • A Dynamic Modeling Method for Smooth Particles with Solid Structure

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0070] This embodiment provides a solid structure smooth particle dynamics modeling method. Taking the two-dimensional planar solid structure as an example, the following describes in detail how to use the SPH method to establish the dynamic model of the solid structure and solve the stress deformation and related physical information of the planar structure.

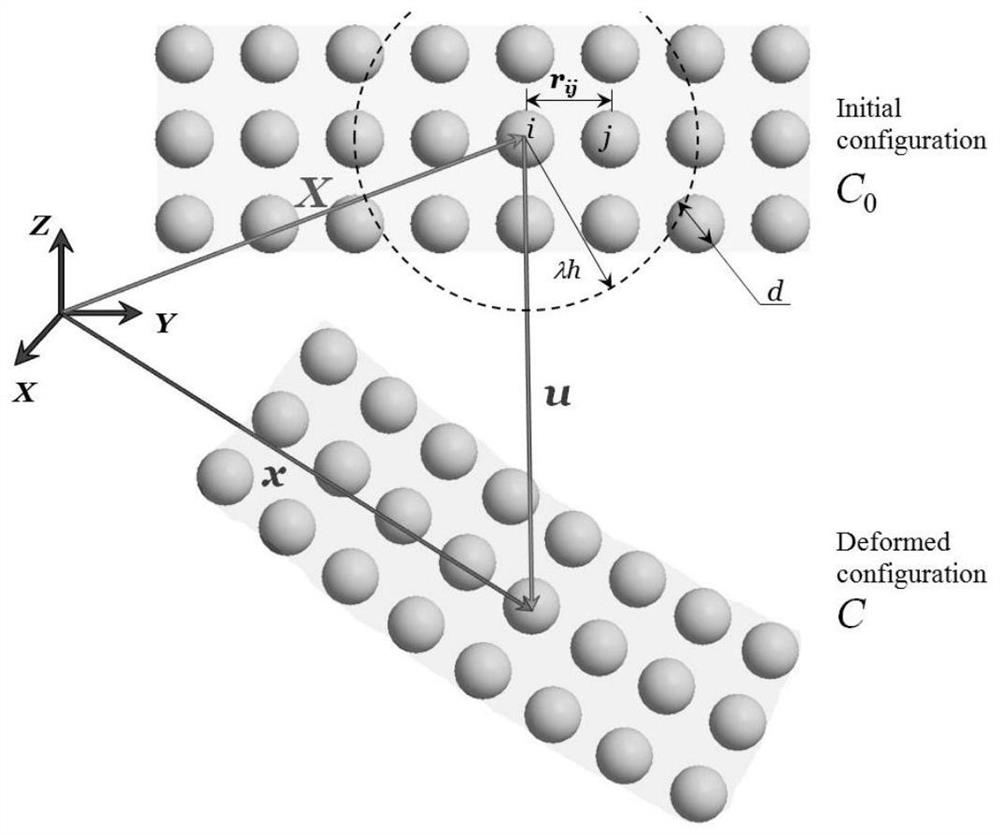
[0071] Step 1: Discretize the planar solid structure into SPH particles, each particle carries at least one kind of the same physical information, such as density, velocity, stress, strain, velocity, etc. figure 1 A schematic diagram of the SPH discrete particles of the planar solid structure provided by an embodiment of the present invention in a deformed state, from figure 1 The SPH discrete particle structure of the solid structure can be seen.

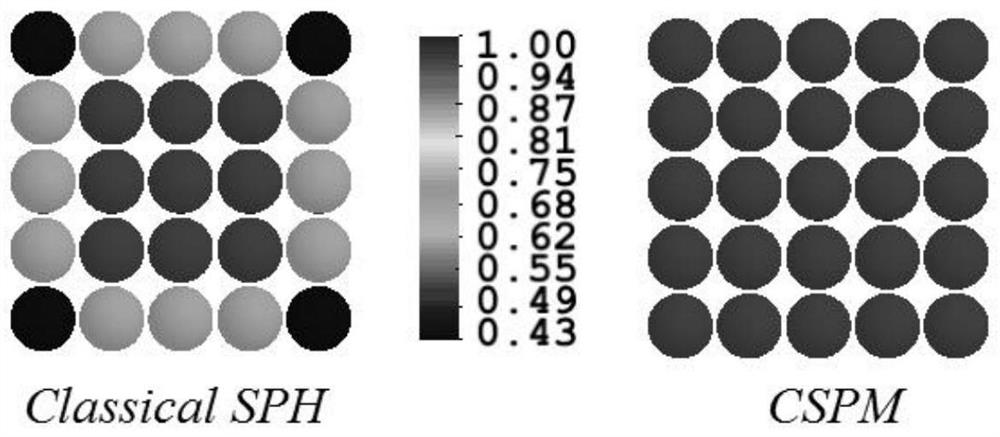
[0072] Step 2: In the deformed state, in order to solve the spatial point x i Deformation occurred at , according to the formula (1) to calculate x i Correction mode for ...

Embodiment 2

[0108] In this embodiment, a dynamic modeling method for solid structure smooth particles is provided. On the basis of the above method, the deformation acceleration of particles is further calculated. The method provided in this embodiment also includes:

[0109] Step 5: Calculate Lagrangian strain and Euler strain according to formula (4) and formula (5):

[0110]

[0111] ε=F -T EF -1 (5)

[0112] Among them, E represents Lagrangian strain, ε represents Euler strain;

[0113] Step 6: Calculate the Cauchy stress according to the plane stress assumption of formula (6):

[0114]

[0115] Among them, σ represents the Cauchy stress;

[0116] Step 7: According to the formula (7), convert the Cauchy stress to the initial undeformed configuration to obtain the first Piola-Kirchhoff stress:

[0117] P=JσF -T (7)

[0118] Among them, P represents the first Piola-Kirchhoff stress, J=|F|, which is the Jacobian determinant;

[0119] Step 8: According to formula (8), calcu...

Embodiment 3

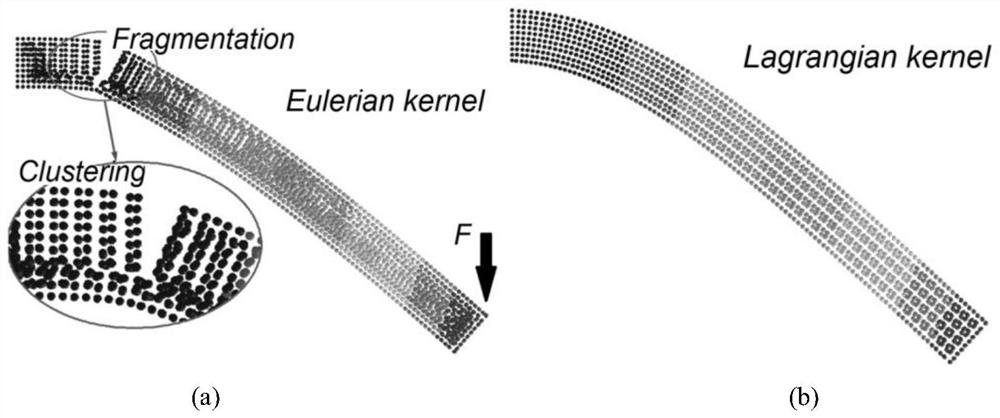
[0131] This embodiment provides a solid structure smooth particle dynamics modeling method, wherein the planar solid structure is an isotropic cantilever arm. Figure 5 Force diagram of an isotropic cantilever beam provided by an embodiment of the present invention. The left end of the beam is fixed and a downward force is applied to the right end. The length, width and height of the beam are 100mm, 1mm and 10mm respectively. Material elastic modulus E = 210GPa, Poisson's ratio υ = 0.3.

[0132] Using the solid structure smooth particle dynamics modeling method provided in Embodiment 1, the planar structure is discretized into 100×10 SPH particles, and the correction of the derivative of the smooth function at the midpoint C of the free edge of the suspended end is calculated according to formula (1) mode, and then solve the deflection of the middle point C of the free side at the right end under different forces. The calculation results are compared with Timoshenko's analy...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

PropertyMeasurementUnit
elastic modulusaaaaaaaaaa
lengthaaaaaaaaaa
Poisson's ratioaaaaaaaaaa
Login to View More

Abstract

The invention relates to the field of materials and provides a dynamic modeling method for solid structure smooth particles. Including: discretize the planar entity structure into SPH particles, each particle carries at least one kind of the same physical information; space point x i Deformation occurs at the place, calculate the space point x i Correction mode of the smooth function derivative at ; then calculate the spatial point x i The deformation at the place; finally in the deformed state, calculate the space point x i deformation gradient at . The present invention combines the corrected smooth function method and the complete Lagrangian SPH method to obtain the corrected model of the derivative of the smooth function as the integral kernel, which ensures the first-order completeness of the numerical method, thereby improving the accuracy of the boundary calculation, and at the same time The stretching instability phenomenon is eliminated, the calculation time is greatly saved, and the boundary defects and instability of traditional SPH are overcome.

Description

technical field [0001] The invention relates to the technical field of materials, and more specifically relates to a dynamic modeling method of solid structure smooth particles. Background technique [0002] Composite materials are structural materials with the highest specific strength currently available, and have the advantages of excellent energy absorption performance, high fatigue life, and low manufacturing cost. Smoothed Particle Hydrodynamics (SPH) integrates discrete particle physical information through the "smooth function" integral kernel, and completes the numerical modeling of laminate impact damage, which overcomes the shortcomings of traditional finite element methods such as large amount of calculation and limited simulation accuracy . [0003] The core of the SPH method is the interpolation theory. It does not need to use any grid when calculating the spatial derivative. Instead, an integral kernel called "smooth function" is used to approximate the "smoo...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/20G06F119/14G06F113/26
Inventor 林军李姣管延锦王广春赵国群富芳艳刘帅
Owner SHANDONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com