Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

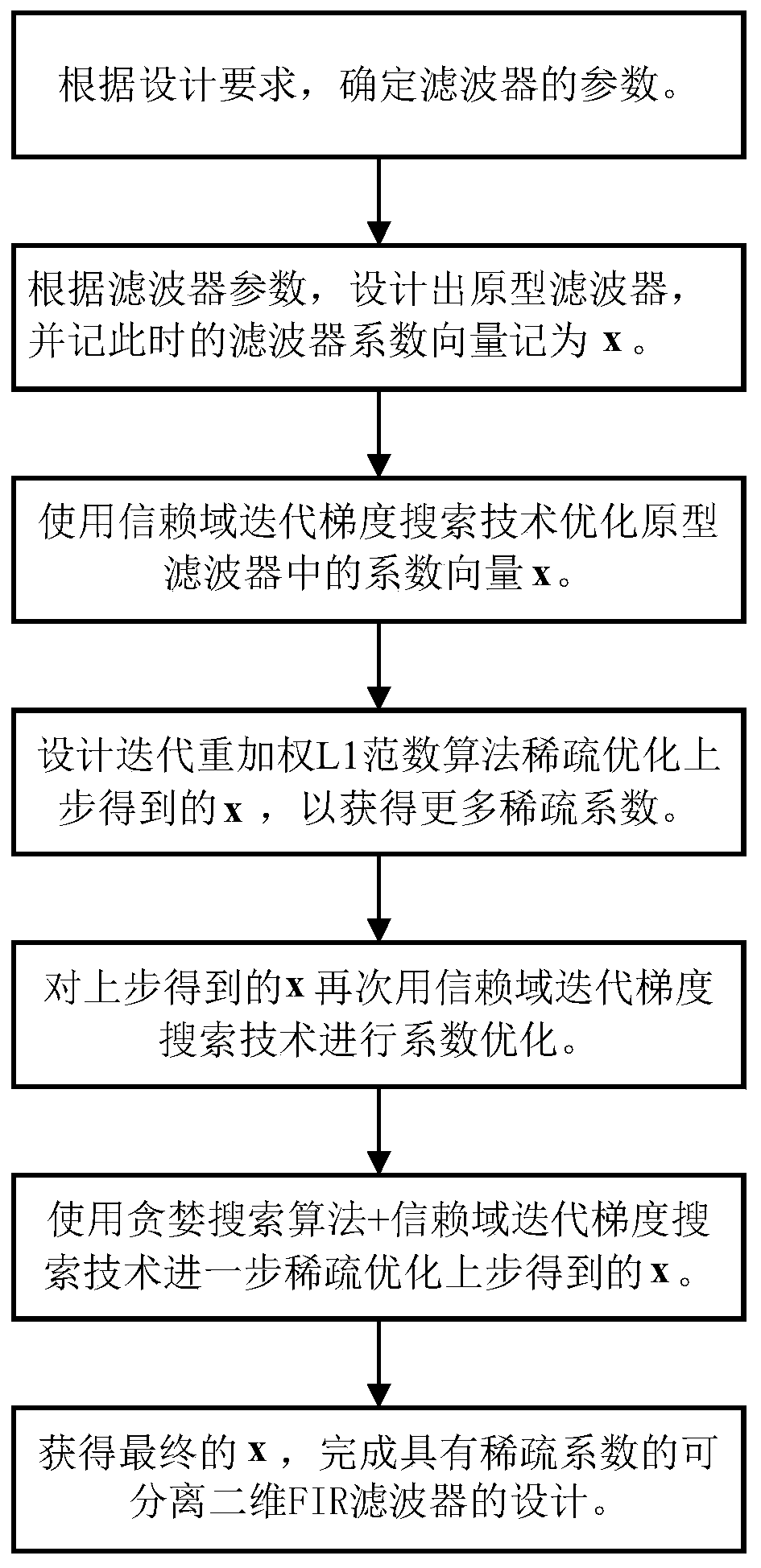
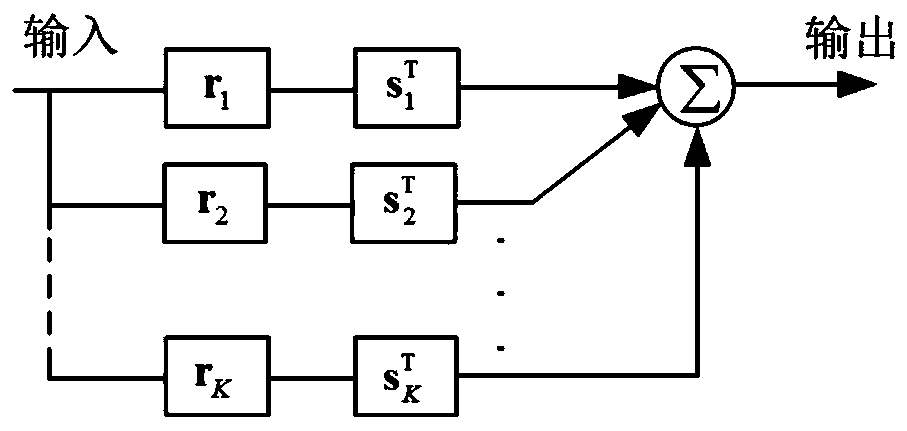
A Design Method for Separable Two-Dimensional FIR Filters with Sparse Coefficients

A technique of sparse coefficients, design methods, applied in design optimization/simulation, computer-aided design, digital technology network, etc.

Active Publication Date: 2020-04-07
HANGZHOU DIANZI UNIV
View PDF6 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Solving the sparse solution is essentially a 0-norm maximization problem, but this is an NP-Hard problem

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Design Method for Separable Two-Dimensional FIR Filters with Sparse Coefficients
  • A Design Method for Separable Two-Dimensional FIR Filters with Sparse Coefficients
  • A Design Method for Separable Two-Dimensional FIR Filters with Sparse Coefficients

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0119] Example 1. Design a quarter-symmetric circular two-dimensional FIR filter, the ideal frequency response is as follows:

[0120]

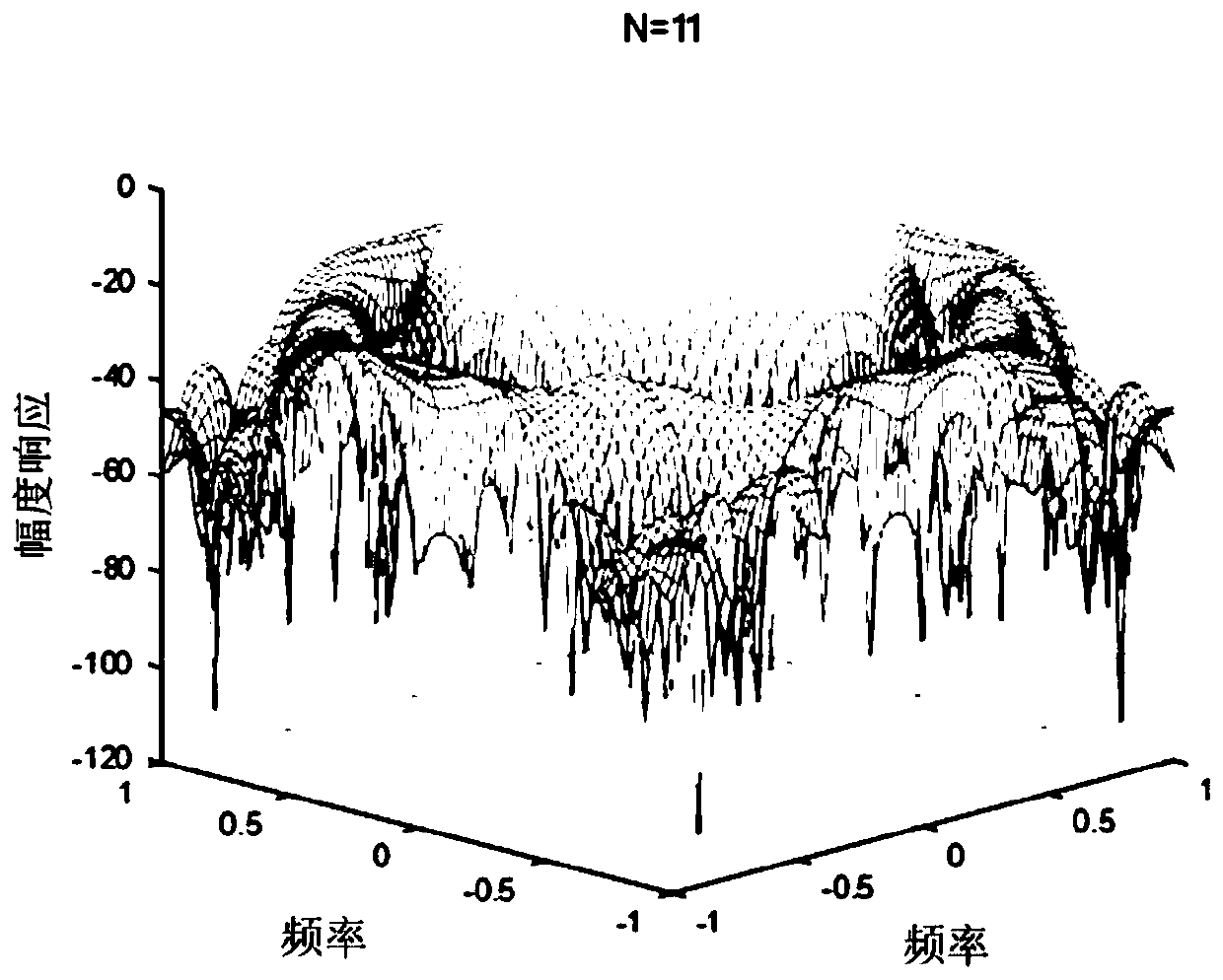
[0121] Where ω p =0.5·π,ω s =0.7·π, the order of the filter is N=11×11, 17×17, 23×23 and 29×29 orders, N 1 And N 2 Satisfy For different orders, the number of frequency sampling points Γ is sequentially set to 1521, 1521, 1521, and 1225; the values ​​of K are 4, 5, 5, and 6 sequentially. The parameter ε=0.15 in step two, and the number of iterations is 10. Parameter ε of step 3 cof_bound = 0.0001, parameter σ = 0.0001, number of iterations is 15. For filters of different orders, the number of iterations in step 5 is 3, 1, 4, and 2 in order. Table 1 shows the results of the separable FIR circular filter with sparse coefficients and the corresponding design parameters. The frequency response is shown in Figure 3(a)-(d);

[0122] Table 1 Design results of a separable two-dimensional FIR circular sparse filter

[0123]

[0124] Note: The prototype...

example 2

[0125] Example 2. Design a quarter-symmetrical diamond two-dimensional FIR filter, the ideal frequency response is as follows:

[0126]

[0127] Where ω p =0.6·π,ω s =π, the order of the filter is N=11×11, 17×17, 23×23 and 29×29 orders, N 1 And N 2 Satisfy For different orders, the number of frequency sampling points Γ is taken as 1521, 1521, 1521, and 1521 in order; the value of K is 5, 5, 5, and 6 in order. The parameter ε=0.15 in step two, and the number of iterations is 10. Parameter ε of step 3 cof_bound = 0.0001, parameter σ = 0.0001, number of iterations is 15. For filters of different orders, the number of iterations in step 5 is 2, 4, 1, and 1 in order. Table 2 shows the results of the designed separable FIR diamond filter with sparse coefficients and the corresponding design parameters. The frequency response is shown in Figure 4(a)-(d);

[0128] Table 2 Design results of a separable two-dimensional FIR diamond sparse filter

[0129]

[0130] It can be seen from Table...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a design method of a separable two-dimensional FIR filter with sparse coefficients, which involves an iterative reweighting l 1 A sparse algorithm combining norm and greedy search technique. The present invention is different from the method in the past, has used sparse algorithm in the design of separable two-dimensional FIR filter for the first time, because the frequency response function of separable two-dimensional FIR filter is a non-convex problem, l 1 The norm method cannot be directly applied, so the present invention solves this problem by fixing some coefficients while maximizing the number of zero-valued coefficients in the remaining coefficients. The invention has the advantages of reducing the hardware complexity of the two-dimensional FIR filter, improving the signal processing efficiency, and integrating the trust region iterative gradient search technology in the design process, so that the coefficients of the filter are more accurate, and the obtained The filter performance index is more superior.

Description

Technical field [0001] The invention belongs to the technical field of digital signal processing, and specifically relates to an iterative reweighting Design method of separable two-dimensional FIR sparse filter combining norm and greedy search technology. Background technique [0002] As an important part of two-dimensional digital signal processing, two-dimensional FIR digital filters have been widely used in many aspects such as medical image processing, satellite image processing, radar, sonar, and seismic signal processing. However, the two-dimensional FIR filter has the significant disadvantages of high hardware execution complexity (the hardware execution complexity of the FIR filter is usually measured by the number of multipliers and adders required for hardware implementation) and high group delay, especially when the digital filter frequency When the domain performance requirements are high, the problem of high implementation complexity of the two-dimensional FIR digi...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H03H17/06G06F30/20
CPCH03H17/06H03H2017/0081G06F30/20
Inventor 王浩李伟琪赵知劲赵晨子李祥振靳一
Owner HANGZHOU DIANZI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com