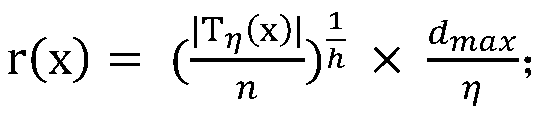Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Three-branch clustering method and system based on improved DBSCAN

A clustering method and clustering technology, applied in the field of data processing, can solve problems such as difficult to fully explain the relationship between objects and classes

Inactive Publication Date: 2019-09-06
重庆亿创西北工业技术研究院有限公司
View PDF0 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Therefore, the hard clustering algorithm DScale-DBSCAN is difficult to fully explain the relationship between objects and classes

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Three-branch clustering method and system based on improved DBSCAN
  • Three-branch clustering method and system based on improved DBSCAN
  • Three-branch clustering method and system based on improved DBSCAN

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

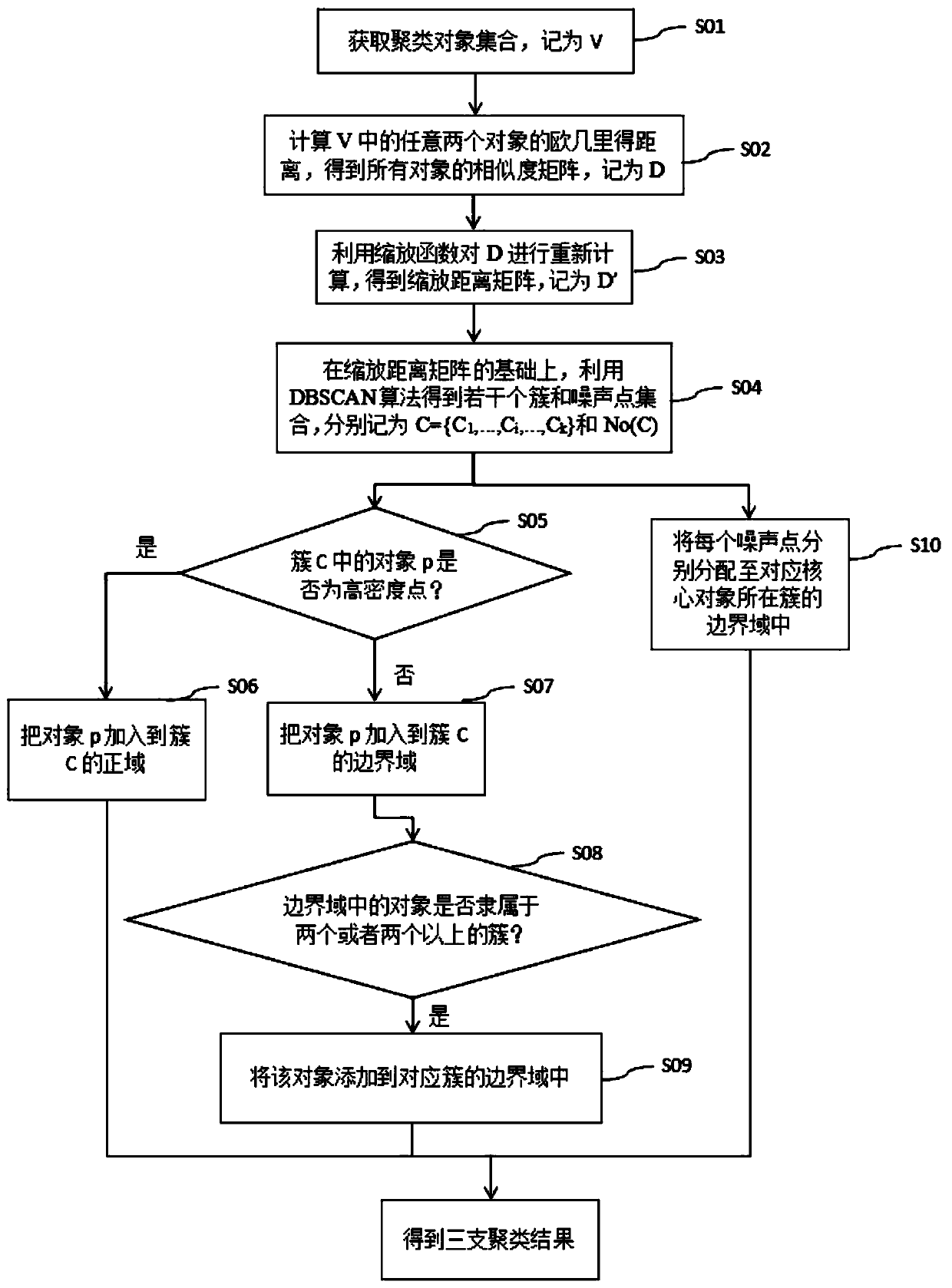
[0045] Reference attached figure 1 This embodiment provides a three-branch clustering method based on improved DBSCAN, which includes the following steps:

[0046] S01. Obtain a set of clustering objects; specifically, obtain objects that need to be clustered, and establish a finite and non-empty set of n clustering objects, denoted as V, where each object has h attributes.

[0047] S02. Calculate the Euclidean distance of any two objects in the clustered object set to obtain the similarity matrix of all objects; specifically, for any two objects x and y in V, use the Euclidean distance formula to get The Euclidean distance between x and y is denoted as d(x,y). The value of d(x,y) represents the similarity of objects x and y. From this, the similarity matrix of all objects can be obtained, Denoted as D. Among them, D=[d(x,y)] n*n , D max Is the largest Euclidean distance in D, d max =max x, y∈V d(x,y).

[0048] S03. Use the scaling function to recalculate the similarity matrix...

Embodiment 2

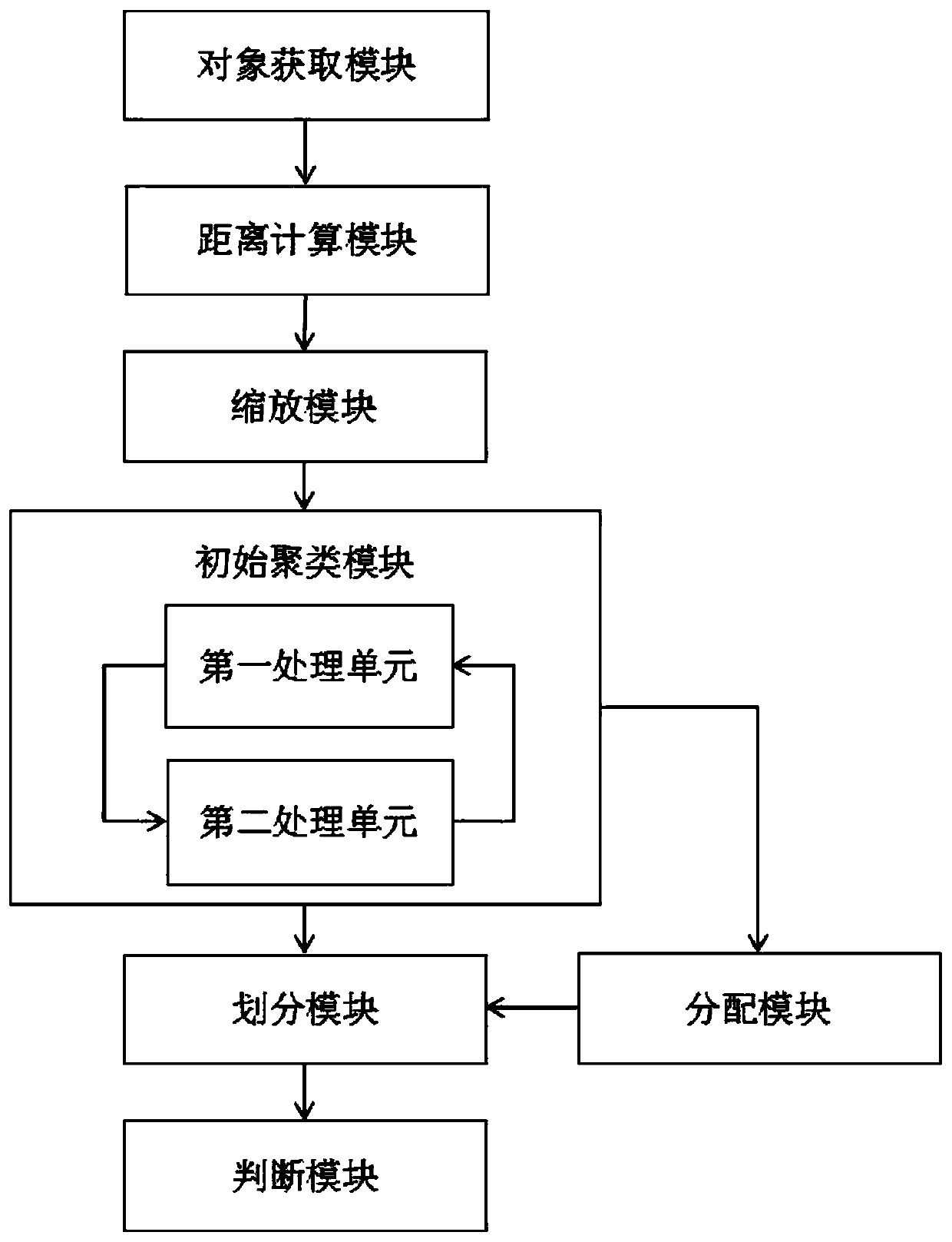
[0077] Reference attached figure 2 This embodiment provides a system for implementing the three-branch clustering method based on the improved DBSCAN provided in the above embodiment 1, which includes: an object acquisition module, a distance calculation module, a scaling module, an initial clustering module, and a division module , Judgment module and allocation module, the initial clustering module includes a first processing unit and a second processing unit.

[0078] Among them, the object acquisition module is used to acquire a clustering object set.

[0079] The distance calculation module is used to calculate the Euclidean distance of any two objects in the clustered object set to obtain the similarity matrix of all objects.

[0080] The scaling module is used to recalculate the similarity matrix using the scaling function to obtain the scaling distance matrix; the scaling function adopted by the scaling module is denoted as r(x), and the calculation formula of r(x) is as fol...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a three-branch clustering method and system based on an improved DBSCAN, and belongs to the technical field of data processing. The three-branch clustering method comprises thefollowing steps: calculating Euclidean distances of any two objects in a clustering object set to obtain a similarity matrix of all the objects; recalculating the similarity matrix by utilizing a scaling function to obtain a scaling distance matrix; on the basis of the scaling distance matrix, obtaining a plurality of clusters and a noise point set through a DBSCAN algorithm; determining a positive domain and a boundary domain of each cluster; judging whether the object in the boundary domain of each cluster belongs to two or more than two clusters or not; and allocating each noise point to the boundary domain of the cluster where the corresponding core object is located. According to the three-branch clustering method provided by the invention, a good clustering result can be obtained onmost data sets, the obtained boundary domain is a delay decision result, and the error rate or decision risk of clustering can be reduced in practical application.

Description

Technical field [0001] The invention relates to the technical field of data processing, in particular to a three-branch clustering method and system based on improved DBSCAN. Background technique [0002] Clustering is the process of dividing a collection of physical or abstract objects into multiple classes composed of similar objects, that is, the process of classifying objects into different classes (or clusters). Objects in the same class have great similarities. Objects belonging to different classes are quite different. [0003] In the prior art, the document "Zhu Y., Ting KM, Angelova M. (2018) A Distance Scaling Met hod to Improve Density-Based Clustering. In: Phung D., Tseng V., Webb G., HoB., Ganji M. .,Rashidi L.(eds)Advances in Knowledge Discovery and DataMining.PAKDD 2018.Lecture Notes in Computer Science,vol 10939." discloses a method for improving the performance of density-based clustering using a multi-dimensional distance scaling algorithm, referred to as DScale ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06K9/62
CPCG06F18/23
Inventor 于会陈芦园王星南毛奎涛张洁杨海泽
Owner 重庆亿创西北工业技术研究院有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com