Novel flat-bottom catenary open channel and solving method of hydraulic optimal section thereof
An optimal cross-section and catenary technology, applied in data processing applications, instruments, calculations, etc., can solve problems such as increased construction difficulty, increased construction cost, and no flat-bottomed space to stand
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
example 1
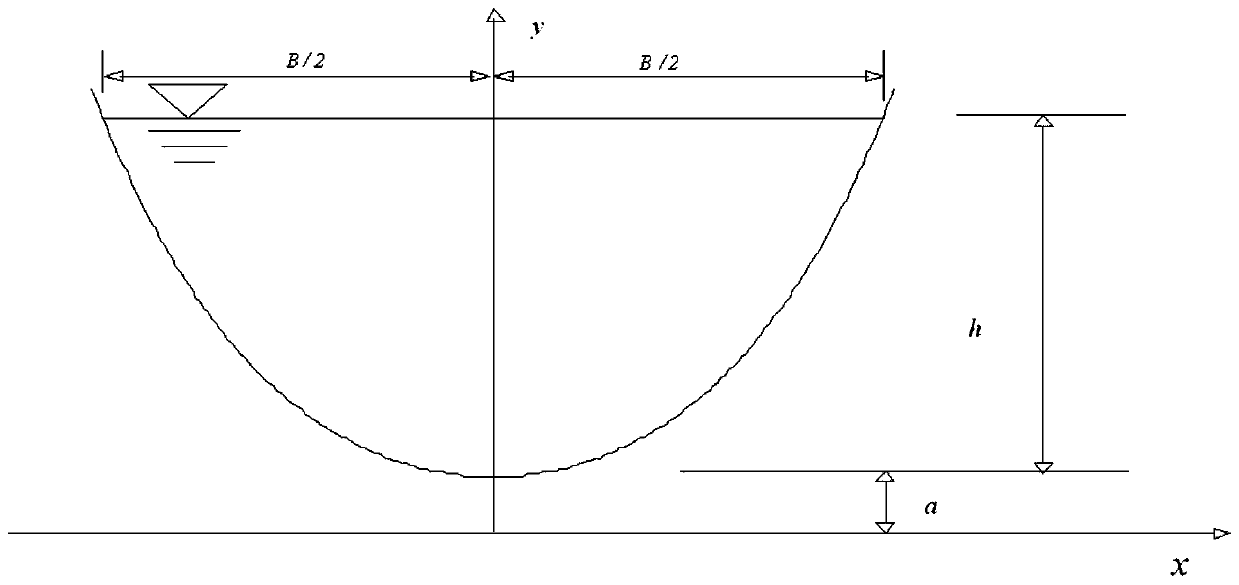
[0321] Example 1: Design an economical and applicable water delivery channel in a water-scarce area in a northern arid area. Design flow 50m 3 / s, bottom slope 1 / 18000, roughness 0.014, slope coefficient z=1.5. According to general channel design principles and construction requirements, the water depth shall not exceed 3m. If a trapezoidal channel is used, due to the stress concentration point between the flat bottom and the slope, it is easy to generate cracks, which will cause leakage and damage to the channel. In addition, the ability to resist frost heave damage is also poor. Therefore, it is easy to adopt the channel section form without stress concentration point. If the traditional catenary section or parabolic section is used, it must be narrow and deep due to the constraints of the curve function, and the water depth exceeds 3m, which is not suitable. Therefore, it is most appropriate to use a flat-bottomed catenary section.
[0322] The water depth is 3.0m. Acc...
example 2
[0323] Example 2: A catenary open channel with flat bottom, i=1 / 11000, Q=17m 3 / s, n=0.014, a=2.1, b=2.5m, find the normal water depth. The present invention adopts Etkin iterative method and quasi-Newton method respectively earlier, has compiled computer program solution formula (10), obtains normal water depth h L = 2.679569365m. Take it as a theoretical reference value, and then solve it with the iterative method proposed by the present invention.
[0324] Set different initial values (h 0 =0.01, 0.1, 1.0, 10, 100), using the deduced explicit Newton iterative method (formula (62)) and simple iterative method (formula (12)) for calculation, the iterative process is as follows Figure 4 shown. The results show that when the initial value of the normal water depth is 0.01, 0.1, 1.0, 10, 100m, the Newton iteration algorithm uses 8, 7, 6, 4, 4, 6 times, while the simple iteration method uses 3, 3, 4, 4, 3, 3 times to make the absolute error less than 0.001m. It can be se...
example 3
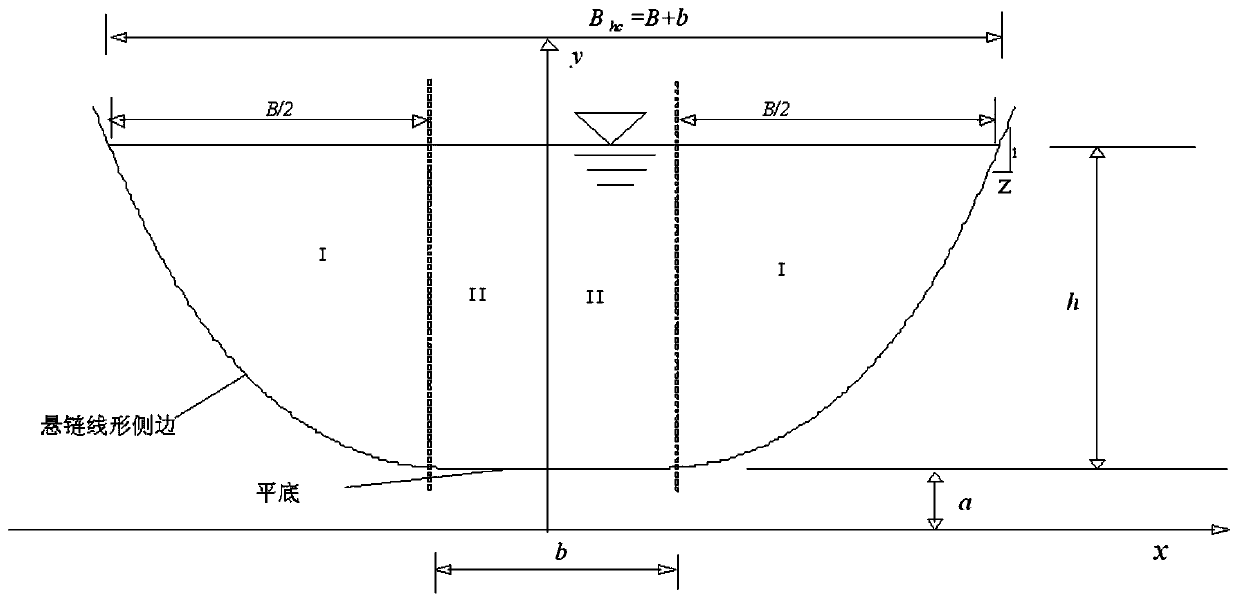
[0328] Example 3: A channel is to be built in a certain place, the known roughness n=0.014, longitudinal slope at the bottom of the channel i=1 / 20000, flow Q=25.0m 3 / s. It is required to design the flat-bottomed catenary channel according to the optimal hydraulic section and calculate the width of the water surface, the cross-sectional area of the water and the wetted perimeter. Substituting known conditions into formulas (40), (33), and (34), the normal water depth h, shape coefficient a, and channel bottom width b can be obtained as h=4.30883m, a=2.04216, and b=1.74579m, respectively. Substituting known conditions into formula (36), we can see that the water surface width B hc = 9.10098m. Substituting the known conditions into formulas (42) and (43) to get A hc =29.67315m 2 , P hc = 13.77319m. The critical water depth h can be obtained from formula (46) c = 2.01187m.
[0329] In order to check the results, the Substitute into Manning formula (9) to get
[0330]...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com