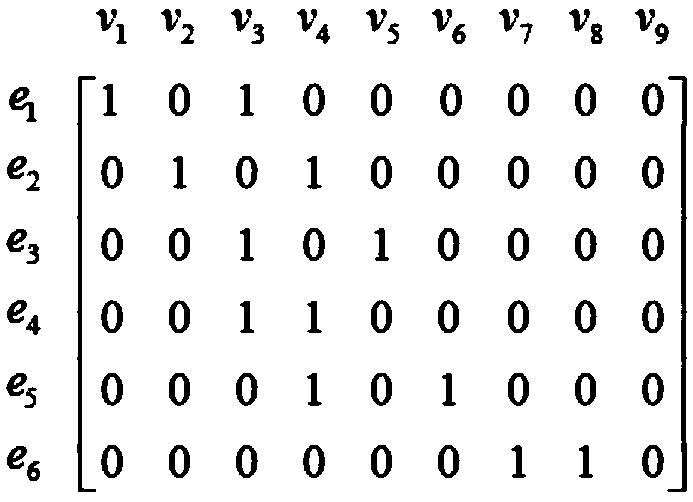Connected piece identification method based on association matrix compression and branch pointer vector update
A technology of correlation matrix and identification method, which is applied to circuit devices, AC network circuits, electrical components, etc., can solve the problems of matrix decomposition process and merging calculation cumbersome, multi-redundant calculation, etc., to achieve efficient and reliable methods, avoid logical operations, Widely applicable effects
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
[0039] like Figure 1 to Figure 7 As shown, the connected slice identification method based on incidence matrix compression and branch pointer vector update includes the following steps:
[0040] Step 1: Generate the branch-node association matrix of the network according to the branch-node related information of the network;
[0041] Step 2: Search the zero column of the branch-node incidence matrix to identify isolated nodes;
[0042] Step 3: "compress" the branch-node correlation matrix by row, and only keep the column labels of non-zero elements to obtain multiple binary connected sets;
[0043] Step 4: Carry out a column scan on the branch-node correlation matrix, and update the branch pointer vector;
[0044] Step 5: According to the final branch pointer vector, the binary connected set is fused and grown to obtain the final set of connected slices.
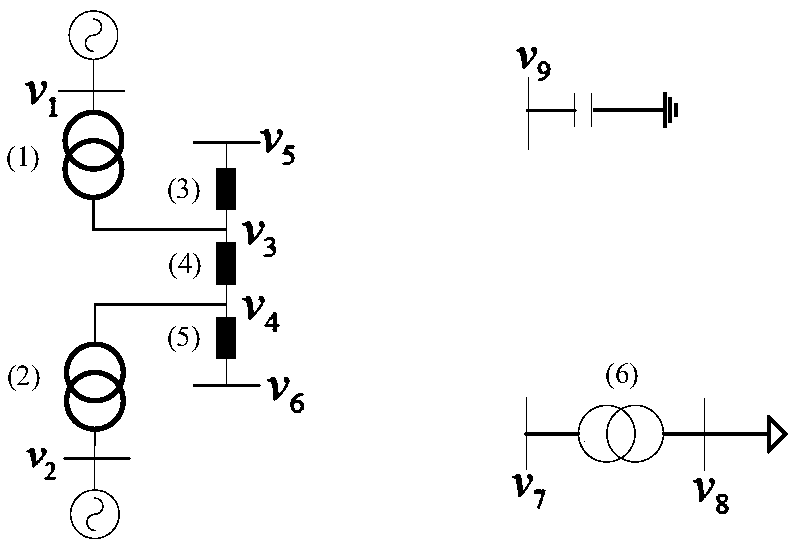
[0045] figure 1 The shown 9-node simplified power system illustrates the method of the present invention. In the fig...
Embodiment 2
[0047] The difference between this embodiment and Embodiment 1 is that the branch-node association matrix of the network is represented by a matrix R of order m×n. When branch i is associated with node j, it is recorded as 1, otherwise it is recorded as 0. The branch-node incidence matrix for the network is a column vector r in R i Scan each element of (i=1,2,…,n), if each element is 0, that is r i = 0, it is an isolated node, named v i (i=1,2,...,n). Obtaining the binary connected set in the step 2 includes the following steps: Step 2.1: row-scanning the branch-node correlation matrix, the row vector r k (k=1,2,...,n), the non-zero elements obtained in the kth row are respectively recorded as r kp 、r kq ;Step 2.2: Take out the non-zero element r in row k kp 、r kq The column numbers p, q form a binary connected set {p, q}, and use the branch e k Representation; Step 2.3: Scan out the binary connected sets of all rows, in the form of The branch pointer vector is an m×1...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com