Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

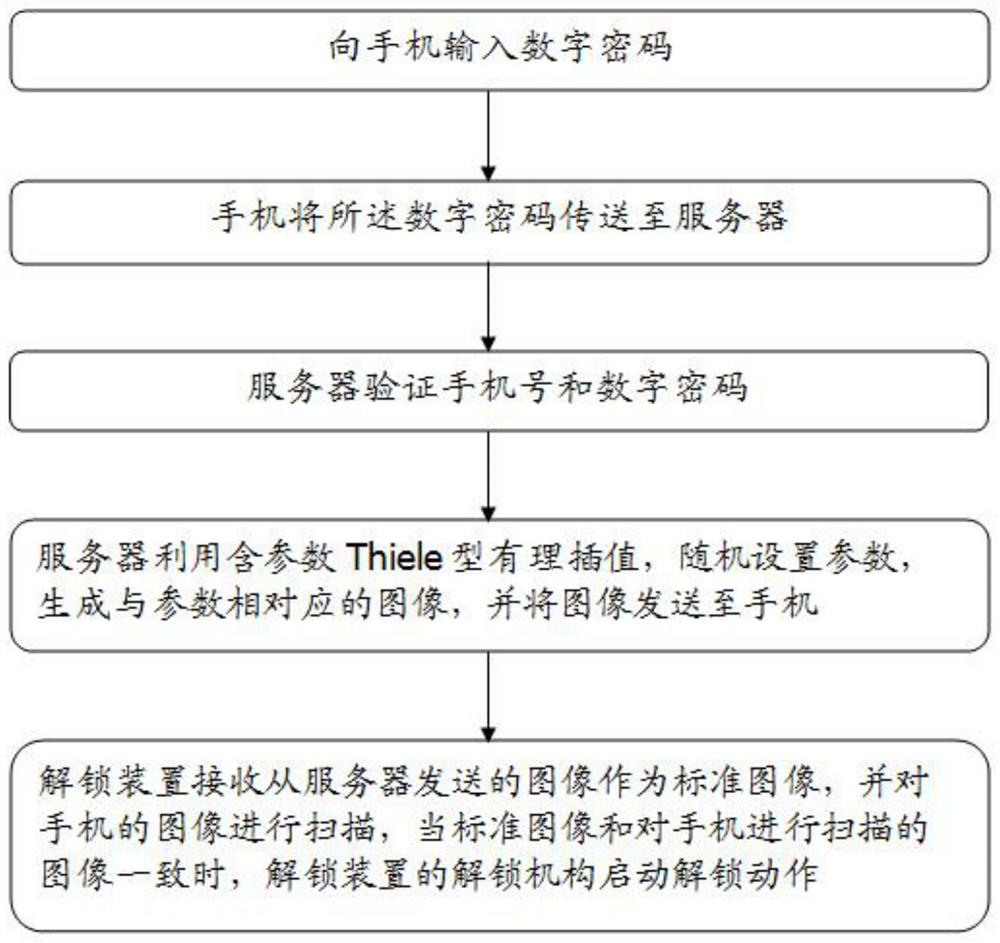
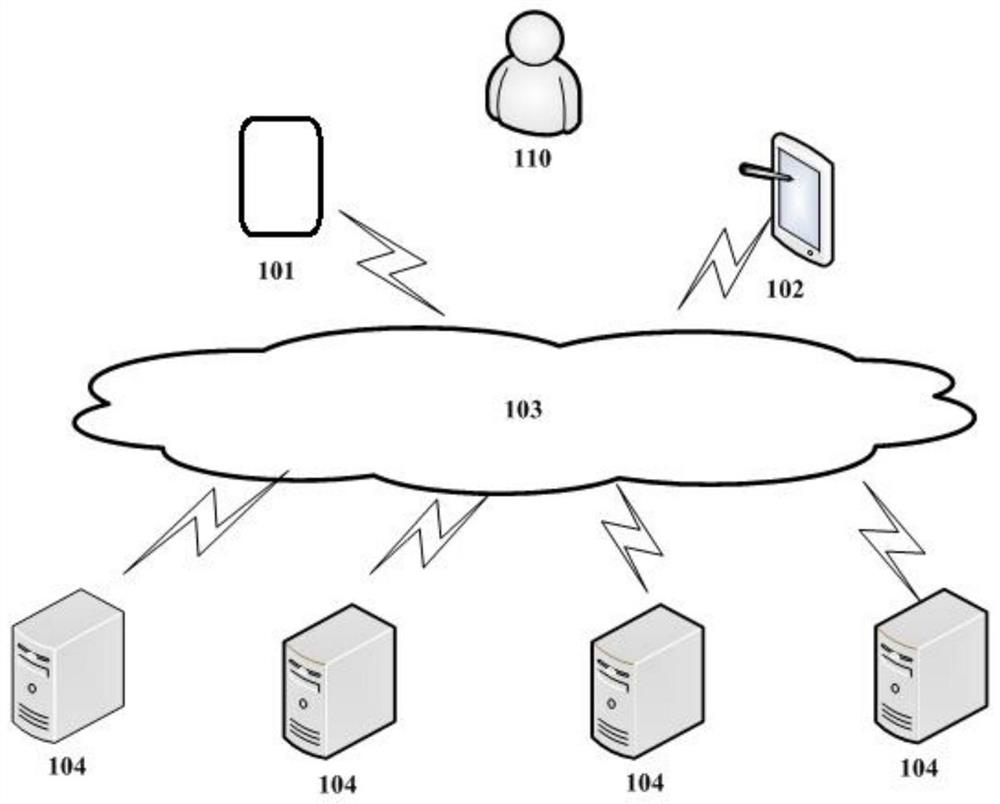
Safe access method and system using rational interpolation with parameter thiele type

A technology of secure access and interpolation, applied in the field of secure access to secure resources, and can solve problems such as leakage

Active Publication Date: 2021-12-10
HEFEI UNIV
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

When there are multiple users, if a unified password is provided, it is easy to cause leakage problems; and if different passwords are provided for different users, it will bring a lot of inconvenience
Therefore, the existing encryption technology cannot meet the above needs, which brings a lot of inconvenience.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Safe access method and system using rational interpolation with parameter thiele type
  • Safe access method and system using rational interpolation with parameter thiele type
  • Safe access method and system using rational interpolation with parameter thiele type

Examples

Experimental program
Comparison scheme
Effect test

example 1

[0163] Example 1 for the function Common high-order continued fraction rational interpolation is unstable, and Thiele continued fraction rational interpolation with parameters is used for calculation. Due to the symmetry of the function, only the interpolation interval [-1,0] is discussed.

[0164] Table 5 Interpolation comparison table

[0165]

[0166]

[0167]

[0168] It can be seen from Table 2 that the Thiele-type continued fraction rational interpolation with parameters has a good effect, and some new Thiele-type continued fraction rational interpolations can also be obtained by selecting parameters.

example 227

[0169] Example 2[27] Set the given point interpolation data {(0,0),(1,1),(2,0.5),(3,3),(4,-0.5),(5,5)}, find Rational interpolation that satisfies the condition.

[0170] After calculating the contrast quotient, if there is a situation where the contrast quotient does not exist, a rational interpolation function can be constructed by adjusting the two nodes (3,3), (4,-0.5) according to the method in the text.

[0171]

[0172] Easy to see R 1 (x) does not meet the interpolation conditions, use the method in this chapter to regard (0,0) as a double node, and introduce the parameter c (c≠0) to get

[0173]

[0174] It is easy to prove that the interpolation condition is met.

example 3

[0175] Example 3 Let the given interpolation data be as follows

[0176] Table 6 Interpolation data table

[0177]

[0178] The corresponding Thiele-type continued fraction interpolation deficit quotient table is shown in Table 8

[0179] Table 7 Deficit Quotient Table

[0180]

[0181] Thus its Thiele-type continued fraction interpolation is Since r(x 0 )=r(2)=0≠1, so (2,1) is an unreachable point of r(x). According to the algorithm in this chapter, increase the multiplicity of the node (2,1), construct a tangential interpolation with a first-order derivative at the point (2,1), introduce the parameter λ (λ≠0), and construct the deficit quotient shown in Table 4 above table, so as to obtain the corresponding Thiele-type tangent rational interpolation

[0182]

[0183] after verification,

[0184] R 2 (x i ) = f i (i=0,1,2)

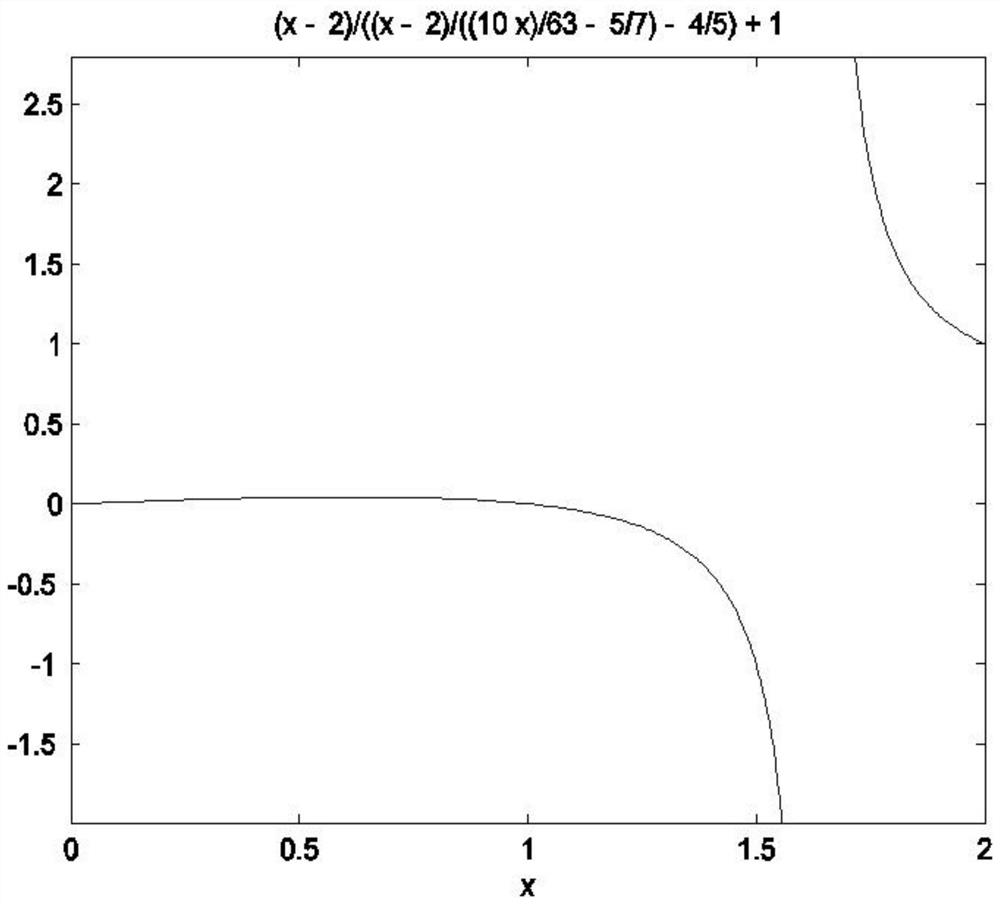
[0185] When λ=-0.8

[0186]

[0187] When λ=80

[0188]

[0189] When λ=-0.8, R 2 The image of (x) is attached figure 1 As ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present application discloses a safe access method and system using Thiele type continued fraction rational interpolation with parameters. The safe access method comprises the steps of: inputting a digital password to a mobile phone; the mobile phone transmits the digital password to a server; the server verifies the mobile phone number and the digital password, and for the verification of the mobile phone number and the digital password, the following steps are performed: Operation: The server takes the digits of the digital password as the corresponding given interpolation data, uses Thiele-type rational interpolation with parameters, randomly sets the parameters of Thiele-type rational interpolation, and generates the corresponding parameters. image, and send the image to the mobile phone; the unlocking device receives the image sent from the server as a standard image, and scans the image of the mobile phone, when the standard image and the scanned mobile phone When the images are consistent, the unlocking mechanism of the unlocking device starts an unlocking action.

Description

technical field [0001] The present disclosure generally relates to the technical field of secure access to secure resources, and in particular to a secure access method and system using Thiele-type rational interpolation with parameters. Background technique [0002] Typically, in secure resource systems such as doors, computers and other devices, the security device will be unlocked when a user's identity and access rights are verified by an authentication device physically connected to the door, computer and other device. When there are multiple users, if a unified password is provided, it is easy to cause a leakage problem; and if different passwords are provided for different users, it will bring a lot of inconvenience. Therefore, the existing encryption technology cannot meet the above-mentioned needs, which brings a lot of inconvenience. Contents of the invention [0003] In view of the above defects or deficiencies in the prior art, it is desired to provide a secur...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H04L9/32H04L9/08H04L29/06
CPCH04L9/0861H04L9/3226H04L9/3234H04L63/083H04L63/0853
Inventor 邹乐宋良图陈艳平王晓峰檀明张洁黄前静
Owner HEFEI UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com