Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for realizing quantum circuit design through quantum Fourier transform

A technology of Fourier transform and circuit design, applied in the field of circuit design, can solve the problem of high complexity of electronic circuit design

Inactive Publication Date: 2017-08-08
GUANGXI NORMAL UNIV
View PDF5 Cites 16 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0028] The invention provides a method for realizing quantum circuit design by quantum Fourier transform, which solves the problem of high complexity in realizing electronic circuit design by conventional classical fast Fourier transform

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for realizing quantum circuit design through quantum Fourier transform
  • Method for realizing quantum circuit design through quantum Fourier transform
  • Method for realizing quantum circuit design through quantum Fourier transform

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0070] A method for realizing quantum circuit design through quantum Fourier transform, comprising the steps of:

[0071] Step 1: Combine quantum computing with classical Fourier transform techniques to obtain quantum Fourier transform.

[0072] The specific process is: Step 1.1: A set of standard orthogonal basis |0>,...,|2 n -1> acts on the ground state |k> to obtain the discrete quantum Fourier transform where k∈{0,1,...,2 n -1}, i is an imaginary unit, n and j are integers;

[0073] Step 1.2: Take the discrete quantum Fourier transform Acting on the quantum state |ψ>, the action process is in is a complex number, i is the imaginary unit, n and j are integers, θ k is a real number;

[0074] Step 1.3: Simplify the result of the action in step 1.2 to obtain the iterative formula of the quantum Fourier transform

[0075]

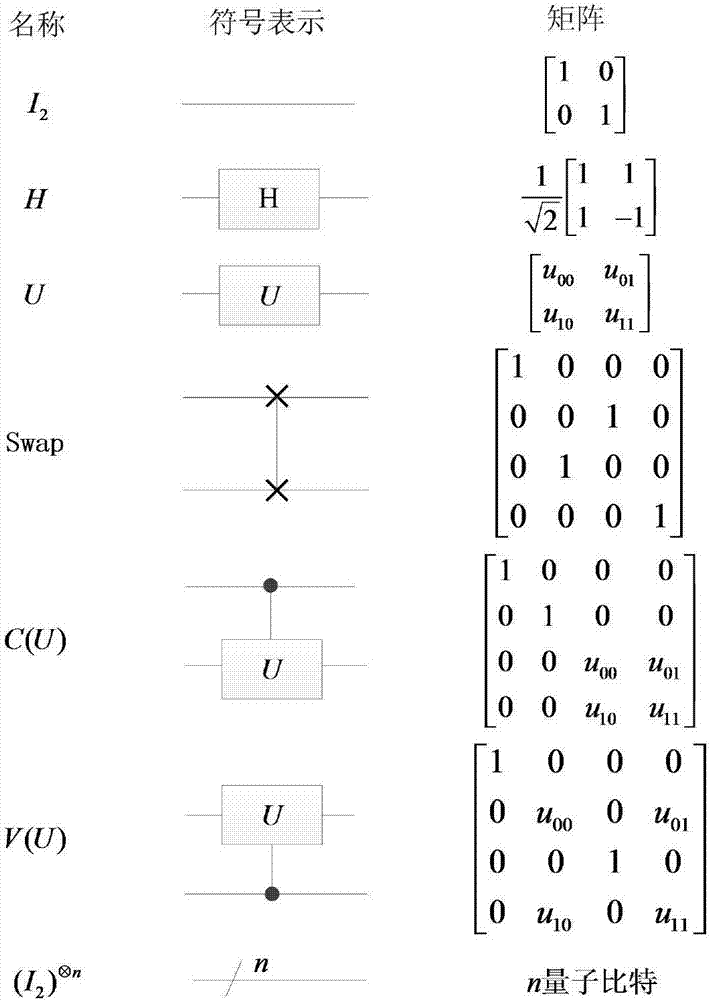
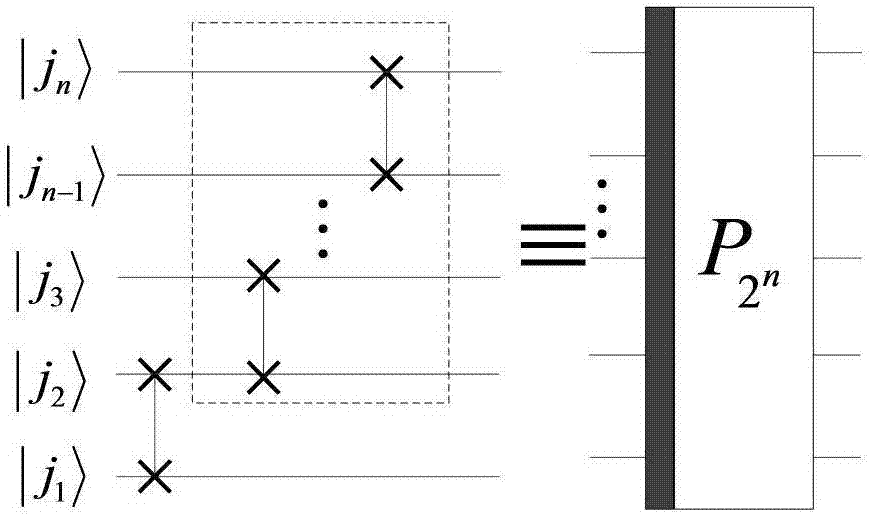
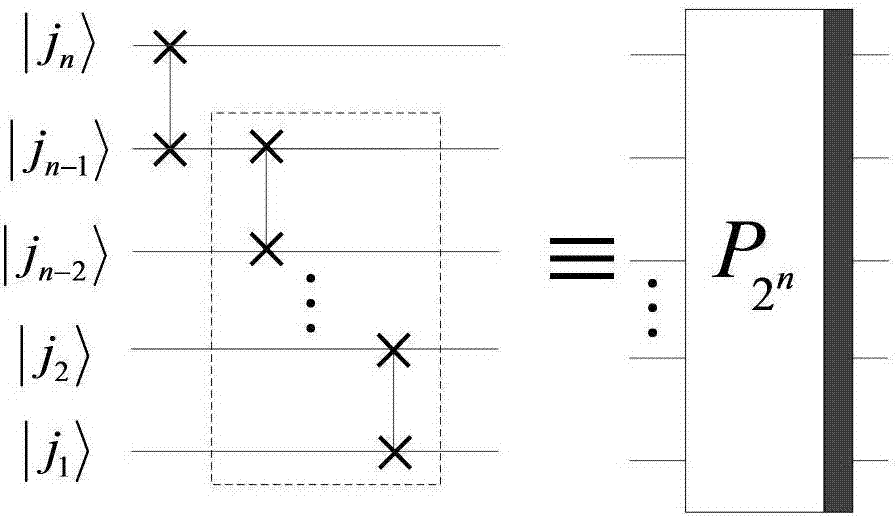
[0076] where H and I 2 is a single-qubit gate, is the tensor product operation symbol, is a uniform shuffling permutation matrix, ...

Embodiment 2

[0093] A method for realizing quantum circuit design through quantum Fourier transform, comprising the steps of:

[0094] Step 1: Combine quantum computing with classical Fourier transform techniques to obtain quantum Fourier transform.

[0095] The specific process is: Step 1.1: A set of standard orthogonal bases |0>,...,|2 n -1> acts on the ground state |k> to get the discrete quantum Fourier transform where k∈{0,1,…,2 n -1}, i is an imaginary unit, n and j are integers;

[0096] Step 1.2: Take the discrete quantum Fourier transform Acting on the quantum state |ψ>, the action process is in is a complex number, i is the imaginary unit, n and j are integers, θ k is a real number;

[0097] Step 1.3: Simplify the result of the action in step 1.2 to obtain the iterative formula of the quantum Fourier transform

[0098]

[0099] where H and I 2 is a single-qubit gate, is the tensor product operation symbol, is a uniform shuffling permutation matrix, and t...

Embodiment 3

[0125] A method for realizing quantum circuit design through quantum Fourier transform, comprising the steps of:

[0126] Step 1: Combine quantum computing with classical Fourier transform techniques to obtain quantum Fourier transform.

[0127] The specific process is: Step 1.1: A set of standard orthogonal bases |0>,...,|2 n -1> acts on the ground state |k> to obtain the discrete quantum Fourier transform where k∈{0,1,...,2 n -1}, i is an imaginary unit, n and j are integers;

[0128] Step 1.2: Take the discrete quantum Fourier transform Acting on the quantum state |ψ>, the action process is in is a complex number, i is the imaginary unit, n and j are integers, θ k is a real number;

[0129] Step 1.3: Simplify the result of the action in step 1.2 to obtain the iterative formula of the quantum Fourier transform

[0130]

[0131] where H and I 2 is a single-qubit gate, is the tensor product operation symbol, is a uniform shuffling permutation matrix, ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a method for realizing quantum circuit design through quantum Fourier transform and belongs to the field of circuit design. A conventional quantum Fourier transform implementation technology is perfected and improved with the method due to the fact that a Bit Reverse circuit is absent in conventional quantum Fourier transform implementation circuits. Four quantum Fourier transform implementation circuits are constructed by an extended tensor product and basic quantum bit gates including quantum bit controlled gates and single quantum bit gates; on the basis of analysis for complexity of the quantum Fourier transform implementation circuits, complexity of the four quantum Fourier transform implementation circuits is theta(n<2>) in terms of a data set comprising 2<n> elements, which cannot be achieved by any other classic fast Fourier transform. The method is suitable for many application fields of actual information processing, for instance, efficient Fourier transform is required for algorithms of image compression, denoising, encryption, decryption and the like, and the method has great significance in perfection of the quantum computing theory and popularization of application.

Description

technical field [0001] The invention relates to the field of circuit design, in particular to a method for realizing quantum circuit design through quantum Fourier transform. Background technique [0002] Quantum computing is the product of the combination of quantum mechanics and computer science. The parallelism, superposition and measurement uncertainty of quantum computing are fundamental to the superiority of quantum computers over classical computers. In the face of such advantages, the research on quantum information processing is very necessary. It has become the focus of strategic competition among countries in the world. Quantum Fourier transform is the core algorithm of quantum information processing. For example, in the quantum algorithm of large number prime factorization and Grover's quantum search algorithm, the quantum Fourier transform is at the key core. [0003] In classical computing, an information unit is represented by a bit (Bit), which has only two ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/14
CPCG06F17/14
Inventor 黎海生夏海英宋树祥范萍
Owner GUANGXI NORMAL UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com