A Best Consistent Approximation Approximation Method for Roll Ring Failure
A processing method and shape technology, applied in metal rolling, manufacturing tools, contour control, etc., can solve the problems of excessive deviation of absolute value, failure to guarantee the minimum absolute value, and failure to ensure the minimum range of local deviation absolute value, etc. To achieve the effect of increasing the yield rate and improving the quality of plate shape control
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0018] The present invention will be further described below in conjunction with accompanying drawing and specific embodiment:
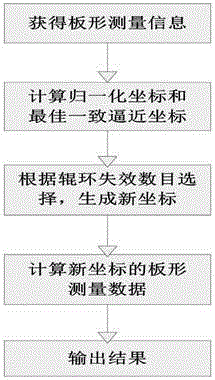
[0019] figure 1 It is a flow chart of the best uniform approximation processing method for a roll ring failure, and its flow is:
[0020] (1) Obtaining flatness measurement information: receiving flatness measurement information from the flatness meter, such as flatness measurement data s(n), number of roll rings n, number of roll ring failures nf, etc.
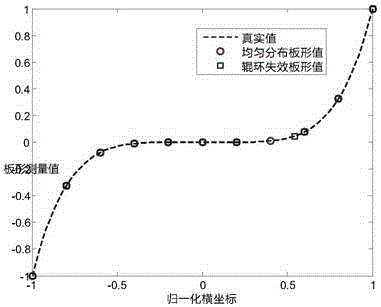
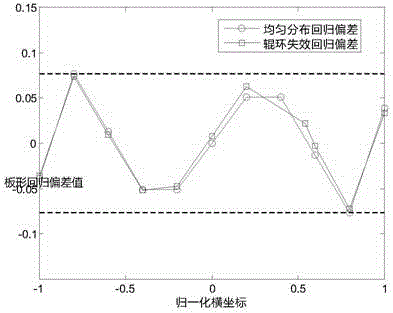
[0021] (2) Calculate the normalized coordinates and the best consistent approximation coordinates: perform normalized calculations according to the number n of roll rings, and calculate the abscissa x(n) of the plate shape, and x(n) is between [-1,1] , generally distributed uniformly with the width of the roll ring, and the spacing is equal; according to Chebyshev's principle and the best consistent approximation condition, the best shape abscissa x'(n) is calculated: x'(n)=cos[(2k- 1) π / 2n], k=1,...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com