Traveling salesman route planning method based on novel shuffled frog leaping algorithm
A hybrid leapfrog algorithm and route planning technology, applied in genetic models, calculations, calculation models, etc., can solve problems such as falling into local optimum, high requirement for step size adjustment accuracy, slow convergence speed, etc.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
[0094] In order to better understand the technical content of the present invention, specific embodiments are given together with the attached drawings for description as follows.
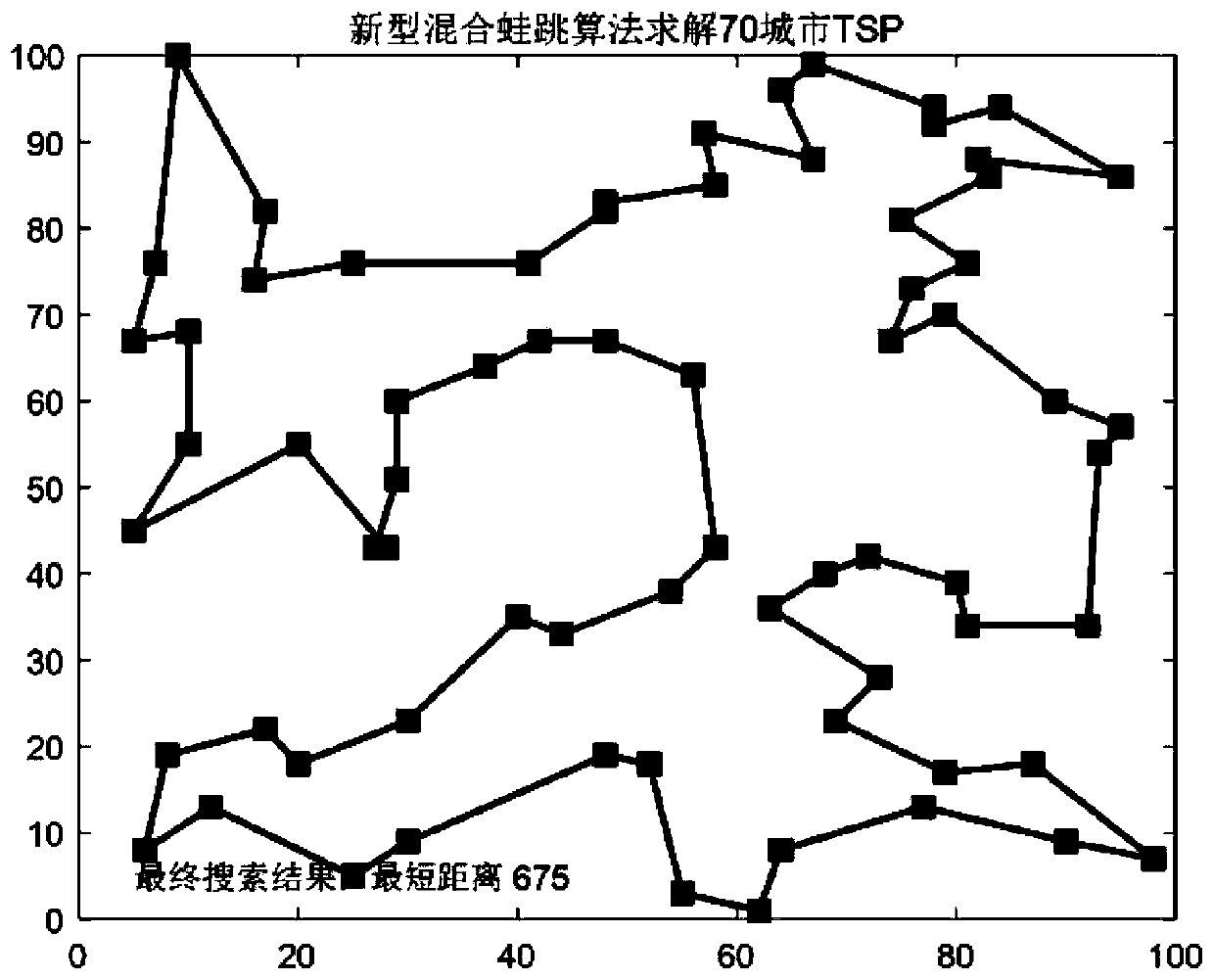
[0095] Select an instance St70 from TSPLIB. There is a traveling salesman who needs to visit 70 cities. The city coordinates (C xi ,C yi ),As shown in Table 1.
[0096] Table 1
[0097] serial number 1 2 3 4 5 6 7 8 9 10 coordinate (64,96) (80,39) (69,23) (72,42) (48,67) (58,43) (81,34) (79,17) (30,23) (42,67) serial number 11 12 13 14 15 16 17 18 19 20 coordinate (7,76) (29,51) (78,92) (64,8) (95,57) (57,91) (40,35) (68,40) (92,34) (62,1) serial number 21 22 23 24 25 26 27 28 29 30 coordinate (28,43) (76,73) (67,88) (93,54) (6,8) (87,18) (30,9) (77,13) (78,94) (55,3) serial number 31 32 33 34 35 36 37 38 39 40 coordinate (82,88) (73,28) (20,55) (27,43) (95,86) (67,99) (48,83) ...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com