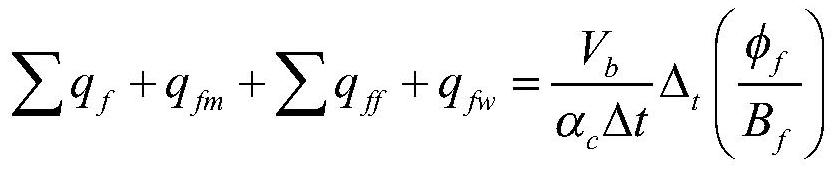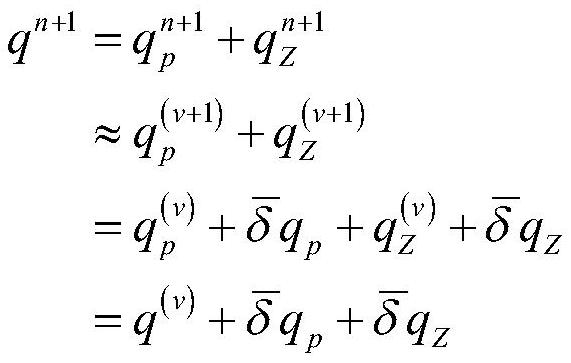Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Mathematical Derivation and Numerical Calculation Method of an Embedded Discrete Fracture Model

A discrete fracture model and numerical calculation technology, applied in the field of reservoir simulation, can solve the problems of different grid seepage equations and difficult mathematical derivation

Active Publication Date: 2020-10-30
SOUTHWEST PETROLEUM UNIV
View PDF7 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, when using the embedded discrete fracture model for numerical simulation research, due to the grids with matrix grids, fracture grids, and well grids, and various flow systems within and between various types of grids, Mass exchange occurs, so the seepage equation of each grid is different, which will cause great difficulties in the process of mathematical derivation and numerical calculation using the embedded discrete fracture model

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Mathematical Derivation and Numerical Calculation Method of an Embedded Discrete Fracture Model
  • A Mathematical Derivation and Numerical Calculation Method of an Embedded Discrete Fracture Model
  • A Mathematical Derivation and Numerical Calculation Method of an Embedded Discrete Fracture Model

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

[0134] In the fully implicit finite difference method, the seepage equations will be discretized and linearized into a polynomial equation system. The unknown of the equation system is the pressure difference between adjacent time steps of each grid. Each polynomial in the equation system is It consists of the mass exchange of a grid with other grids and the final mass accumulation of this grid. Usually the system of polynomial equations is rewritten in the form of matrix equations.

[0135] For the entire process of transforming the governing equations into matrix equations, it is conventional to write out the discretized difference equations for all grids in turn, then list their polynomial forms, and finally assemble them into a matrix. However, for the embedded discrete fracture model, there are two sets of grids, matrix and fracture, and the type and number of grids connected to each grid are unknown, so write directly or pass grid It is impossible to write the seepage e...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a mathematical derivation and numerical calculation method for an embedded discrete fracture model, and the method comprises the following steps: carrying out the derivation and discretization of a seepage differential equation through combining a connection pair theory and a full-implicit finite difference method; assigning and calculating the grid attributes and the basicparameters; based on a grid connection pair theory, establishing a grid connectivity table according to grid positions; in combination with a connectivity table, deriving and calculating a geometrical parameter part of the inter-grid conductivity according to an embedded discrete fracture model theory, and deriving and calculating a weak nonlinear part of the inter-grid conductivity according toa center weighting method; processing the mass exchange item and the mass accumulation item in combination with the connectivity table, and assembling a matrix equation of a seepage differential equation; according to the method, the calculation and derivation difficulty and workload of the embedded discrete fracture model are reduced, a universal method is formed, and the problem that the embedded discrete fracture model is high in calculation difficulty is solved.

Description

technical field [0001] The invention relates to the technical field of reservoir simulation, in particular to a mathematical derivation and numerical calculation method of an embedded discrete fracture model combined with connection pair theory. Background technique [0002] In the development of unconventional oil and gas resources, it is usually necessary to combine multi-stage fracturing horizontal well technology. Due to the extremely complex seepage law of fractured reservoirs, numerical simulation methods are usually used to study the seepage law of such multi-stage fractured horizontal wells. Multi-media numerical simulation methods are divided into continuum model and discrete fracture model, but since the continuum model is only suitable for reservoirs with a large number of micro-fractures connected, it is not suitable for hydraulically fractured reservoirs with strong anisotropy, so the discrete fracture model is often used Research it. The embedded discrete fra...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F30/23G06F111/10G06F119/14
Inventor 刘凌甫赵玉龙张烈辉谢军张芮菡吴建发
Owner SOUTHWEST PETROLEUM UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com