Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

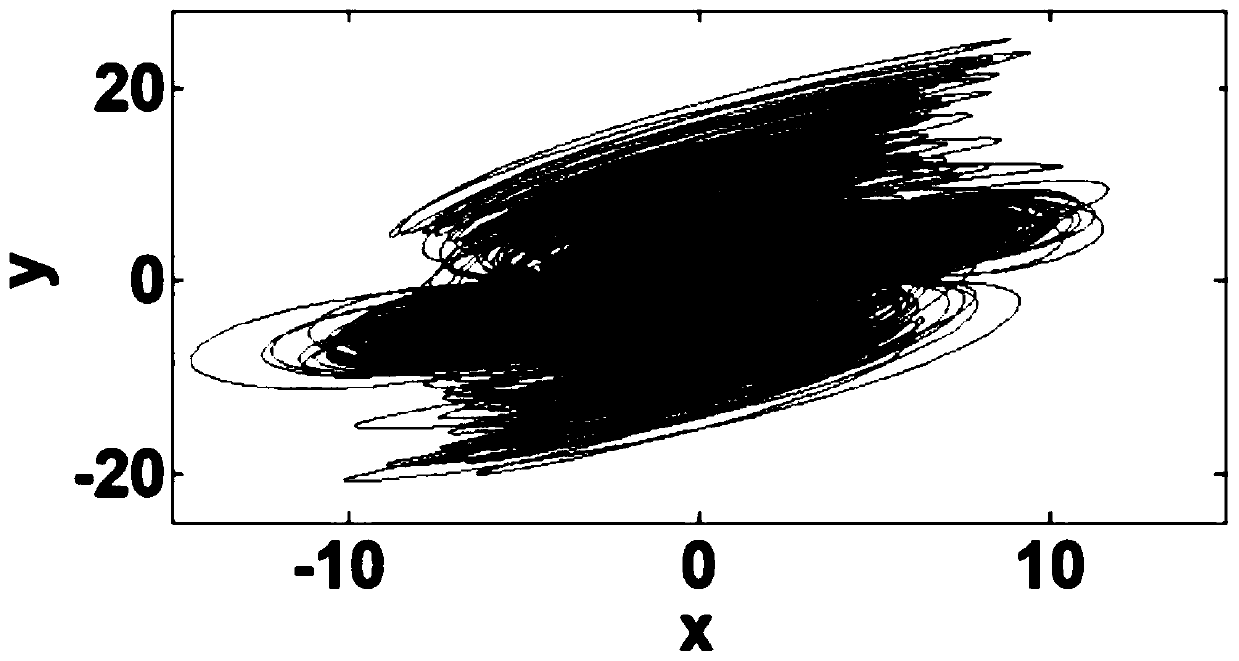
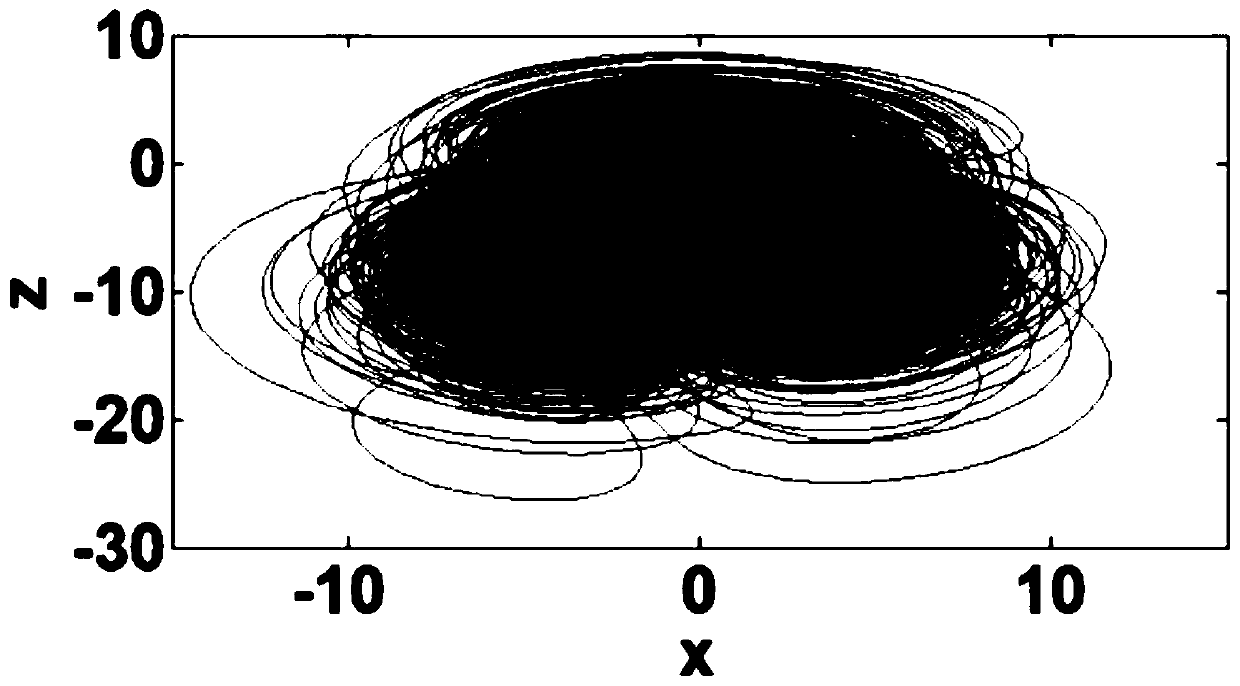
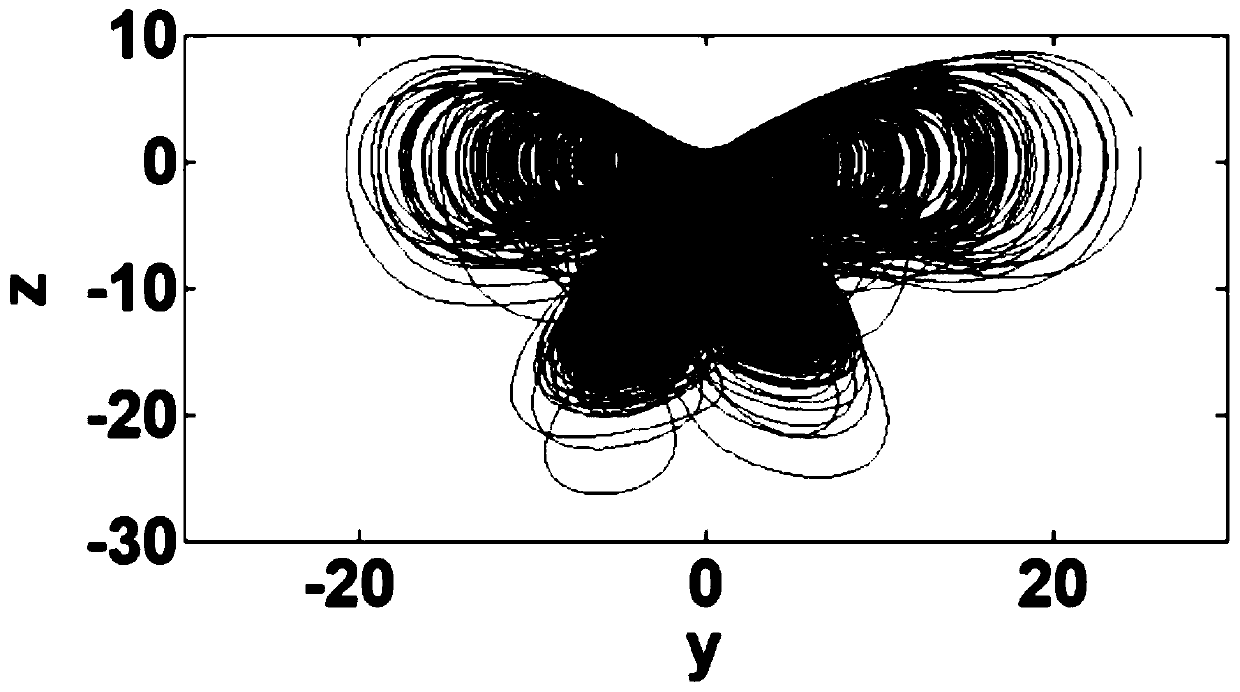
Five-dimensional four-wing memristor hyper-chaotic system and design, analysis and implementation method thereof

A technology of system design and implementation method, applied in computer-aided design, CAD circuit design, calculation, etc.

Active Publication Date: 2020-01-14
CHANGSHA UNIVERSITY OF SCIENCE AND TECHNOLOGY
View PDF3 Cites 4 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, FPGAs are rarely used to implement five-dimensional memristive hyperchaotic systems

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Five-dimensional four-wing memristor hyper-chaotic system and design, analysis and implementation method thereof
  • Five-dimensional four-wing memristor hyper-chaotic system and design, analysis and implementation method thereof
  • Five-dimensional four-wing memristor hyper-chaotic system and design, analysis and implementation method thereof

Examples

Experimental program
Comparison scheme
Effect test

no. 2 example

[0065]

[0066] 1. Balance point and stability analysis

[0067] The equilibrium point of the equation (1) of the five-dimensional four-wing memristive hyperchaotic system can be obtained by solving differential equations; specifically, the right part of the equation (1) of the five-dimensional four-wing memristive hyperchaotic system is zero, its equation expression is:

[0068]

[0069] Through equation (3), it is easy to conclude that the equilibrium point of system equation (1) is the multi-line equilibrium point where b is an integer and n is any real constant.

[0070] multiline balance point The Jacobian matrix at point O of the five-dimensional four-wing memristive hyperchaotic system can be obtained:

[0071]

[0072] According to the Jacobian matrix (4), the characteristic equation of the system equation (1) can be obtained as follows:

[0073]

[0074] Equation (5) can be written as (6)

[0075] λ(λ+1)[λ 3 +m 1 lambda 2 +m 2 λ+m 3 ] = 0 (6)

...

no. 3 example

[0102]

[0103] Designing chaotic systems using analog electronic circuits with discrete components is one of the most commonly used methods today, but the devices in analog circuits are prone to aging and inflexibility, so more and more researchers have begun to focus on digital devices FPGA. FPGA has the characteristics of high-speed computing, high integration, and free design, and can easily generate chaotic signals. Nowadays, many numerical algorithms are used to solve nonlinear differential equations of chaotic systems. Euler's algorithm is the simplest of all algorithms, but it is not very accurate. Heron's algorithm produces more sensitive results than Euler's algorithm. The Runge-Kutta algorithm has the characteristics of high precision, stable calculation process, and easy implementation. Its operation effect is better than other algorithms. The fourth-order Runge-Kutta algorithm is easier to implement than the fifth-order Runge-Kutta algorithm. The fourth-order ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention provides a five-dimensional four-wing memristor hyper-chaotic system and a design, analysis and implementation method thereof. The five-dimensional four-wing memristor hyper-chaotic system has a multi-line balance point and three positive Lyapunov indexes and shows complex dynamic characteristics such as chaos, hyper-chaos, a limit ring and a period. The dynamic behavior of the novelfive-dimensional four-wing memristor hyper-chaotic system is realized by using the balance point, the phase diagram, the Poincare mapping, the Lyapunov exponent diagram and the bifurcation diagram.

Description

technical field [0001] The present invention relates to a design method for a five-dimensional four-wing memristive hyperchaotic system, a method for analyzing a five-dimensional four-wing memristive hyperchaotic system, and a method for realizing a five-dimensional four-wing memristive hyperchaotic system, and also relates to the The designed five-dimensional four-wing memristive hyperchaotic system. Background technique [0002] Nonlinear science is a new interdisciplinary subject that studies the universality of nonlinear phenomena. It runs through almost all disciplines such as meteorology, mathematics, fluid mechanics, complex networks, electronic circuits and social sciences. Chaos is one of the most important achievements of nonlinear science. The quasi-randomness of chaos and its sensitivity to initial value conditions make it have good application prospects in the fields of random number generation, cryptosystem, image encryption and secure communication. In recen...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F30/367G06F30/30
Inventor 余飞刘莉蔡烁何彬永黄园媛
Owner CHANGSHA UNIVERSITY OF SCIENCE AND TECHNOLOGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com