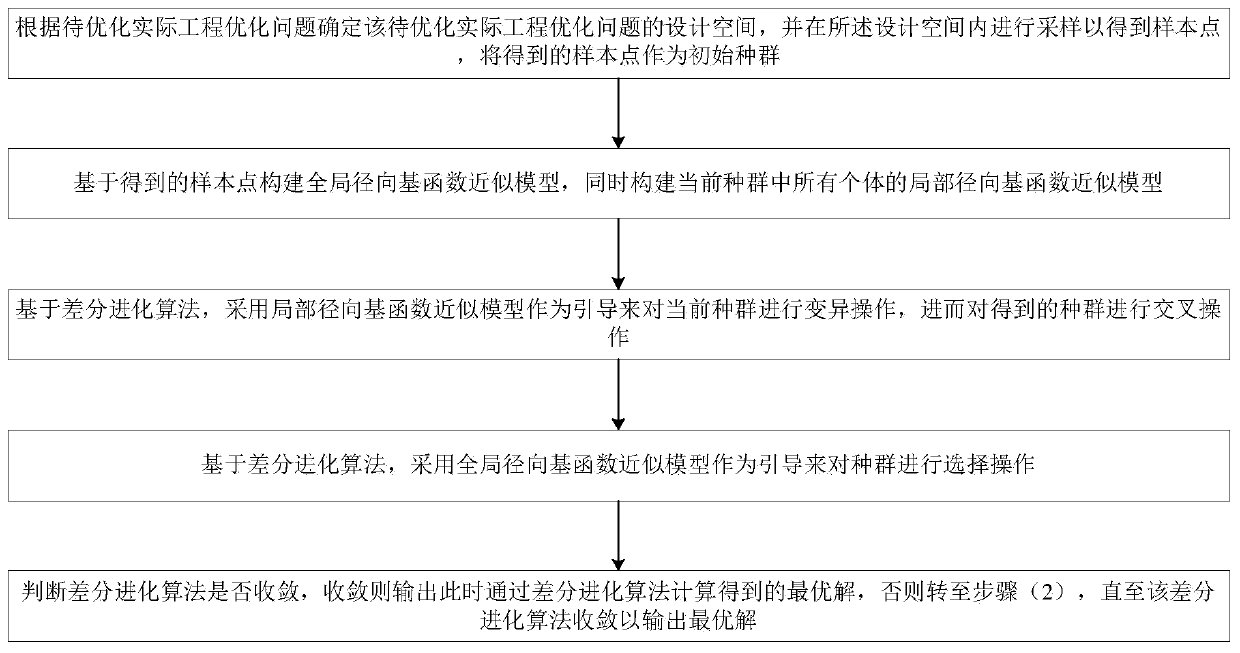
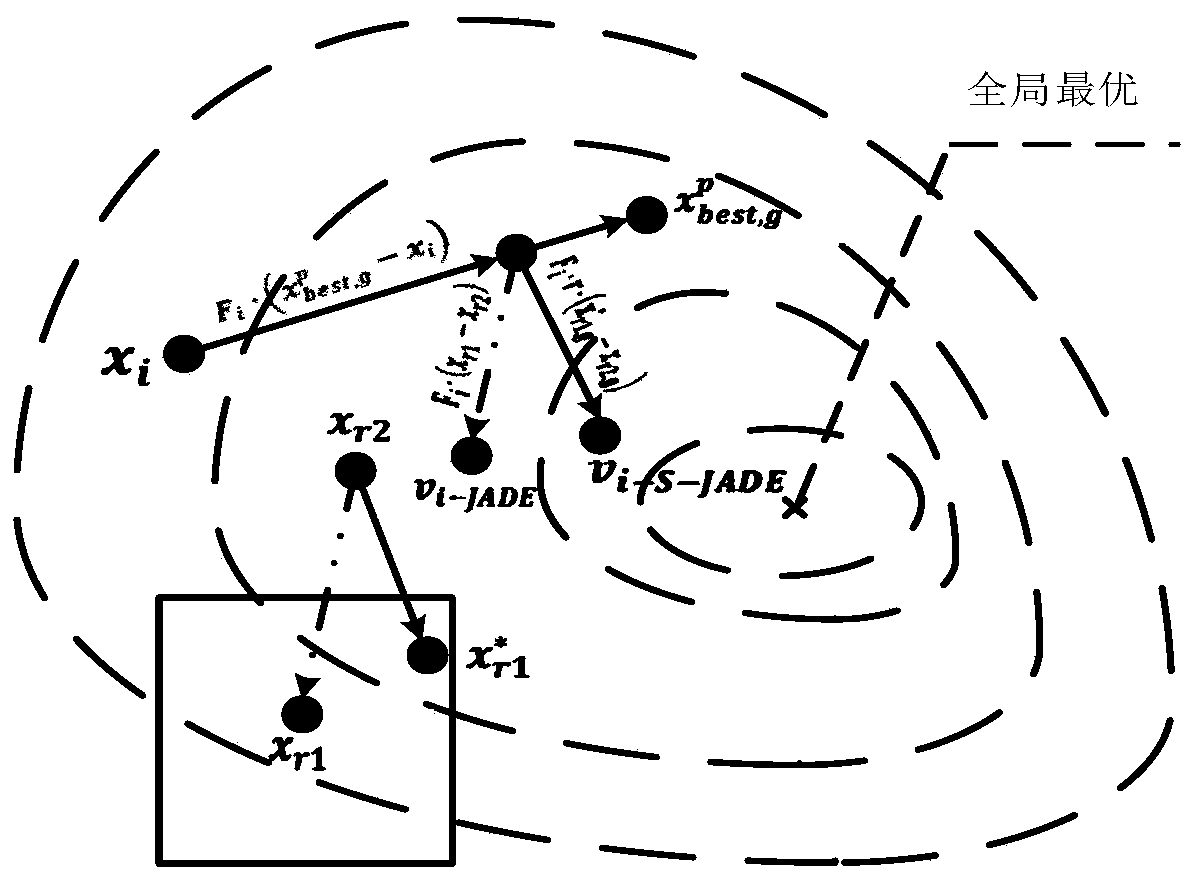
Method for solving high-dimensional optimization problem based on approximation model and differential evolution algorithm

Abstract

The invention belongs to the related technical field of design optimization, and discloses a method for solving a high-dimensional optimization problem based on an approximation model and a differential evolution algorithm. The method comprises the following steps: (1) determining a design space according to a to-be-optimized actual engineering optimization problem; (2) constructing a global radial basis function approximation model and a local radial basis function approximation model of all individuals in the current population based on the obtained sample points; (3) on the basis of a differential evolution algorithm, taking a local radial basis function approximation model as guidance to carry out mutation operation on the current population, and then carrying out crossover operation on the obtained population, and taking a global radial basis function approximation model as guidance to carry out selection operation on the population; and (4) judging whether the differential evolution algorithm converges or not, outputting an optimal solution calculated by the differential evolution algorithm if the differential evolution algorithm converges, otherwise, going to the step (2) until the differential evolution algorithm converges. The method improves the optimization precision, is high in the applicability, and is preferable in the flexibility.

Description

technical field [0001] The invention belongs to the technical field related to design optimization, and more specifically relates to a method for solving high-dimensional optimization problems based on an approximate model and a differential evolution algorithm. Background technique [0002] Engineering optimization problems usually involve computationally expensive simulations and a large number of design variables, although with the development of computing technology, simulation software on finite element analysis (FEA) and computational fluid dynamics (CFD) can alleviate the computational cost in the design process, However, excessive calculation time will still lead to some complex engineering design problems that cannot be optimized. How to solve these problems in an efficient manner remains a great challenge. [0003] In recent years, approximate model-assisted metaheuristic algorithms have been widely studied and are considered to have the potential to solve such en...

AI Technical Summary

Problems solved by technology

[0003] In recent years, approximate model-assisted metaheuristic algorithms have been widely studied and are considered to have the potential to solve such engineering optimization problems. Approximate models have considerable advantages in reducing computational costs, but the usual approximate model-assisted metaheuristics The algorithm cannot meet the accuracy requirements of high-dimensional problems with large-scale variables

Images