MSVL (modeling, simulation and verification language) linear constraint system and implementation method thereof
A linear constraint and execution method technology, applied in data processing applications, prediction, calculation, etc., can solve the problems of insufficient expression ability of linear constraint language
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment 1
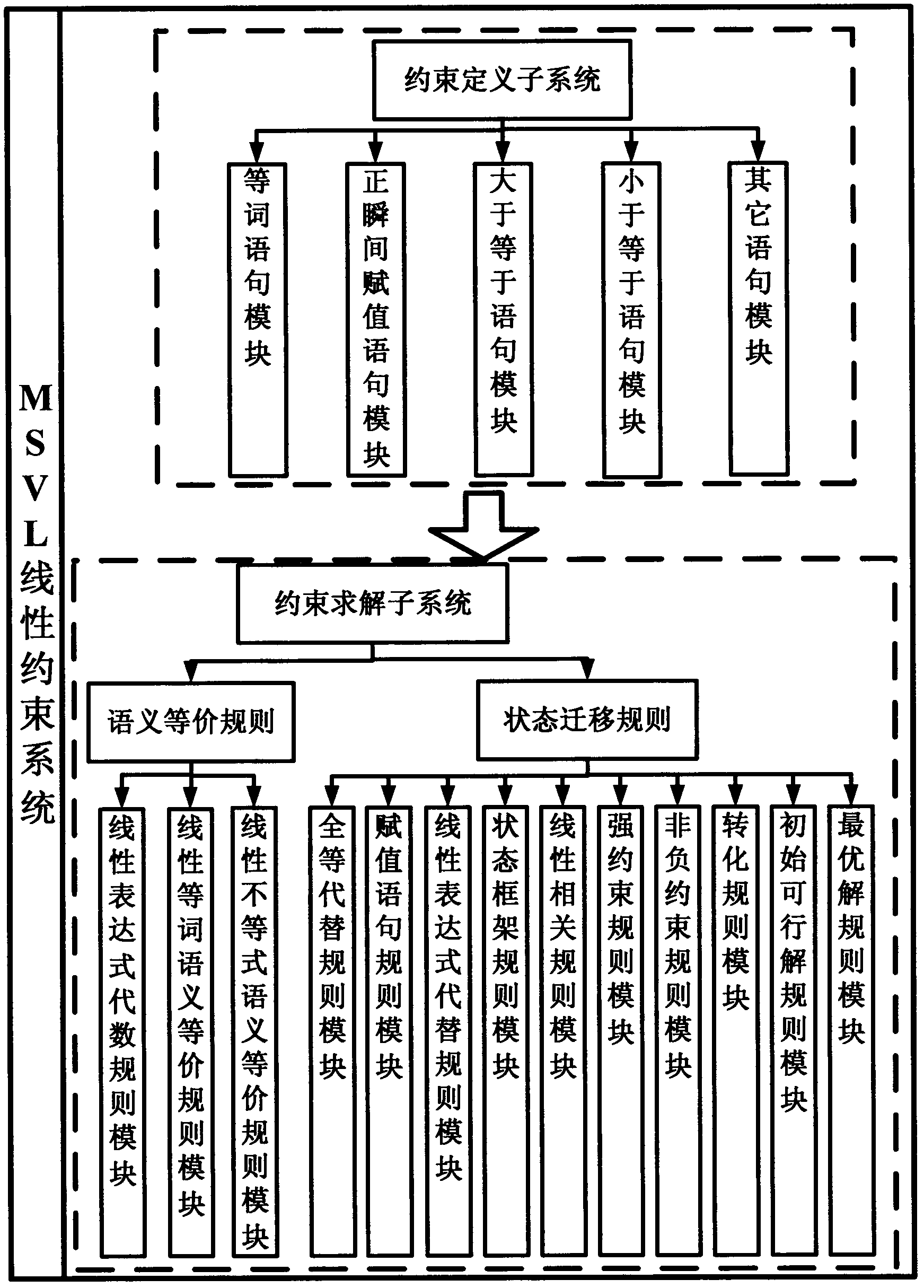
[0082] The invention is an MSVL linear constraint system, which is a modeling and solving system proposed for problems with linear constraints in scientific research and industrial applications. MSVL has been used in software and hardware modeling, simulation and verification, but MSVL lacks a grammatical structure that can describe linear constraints, which widely exist in practical problems, so it is necessary to extend the linear constraint structure in the MSVL system. see figure 1 , the system includes a constraint definition subsystem and a constraint solution subsystem; the constraint definition subsystem is a linear constraint statement module defined on the basis of a linear expression, including an equal word statement module (=), a positive instantaneous assignment statement module Greater than or equal statement module (≥), less than or equal to statement module (≤) and other statement modules; the constraint solving subsystem includes a semantic equivalence rule ...
Embodiment 2
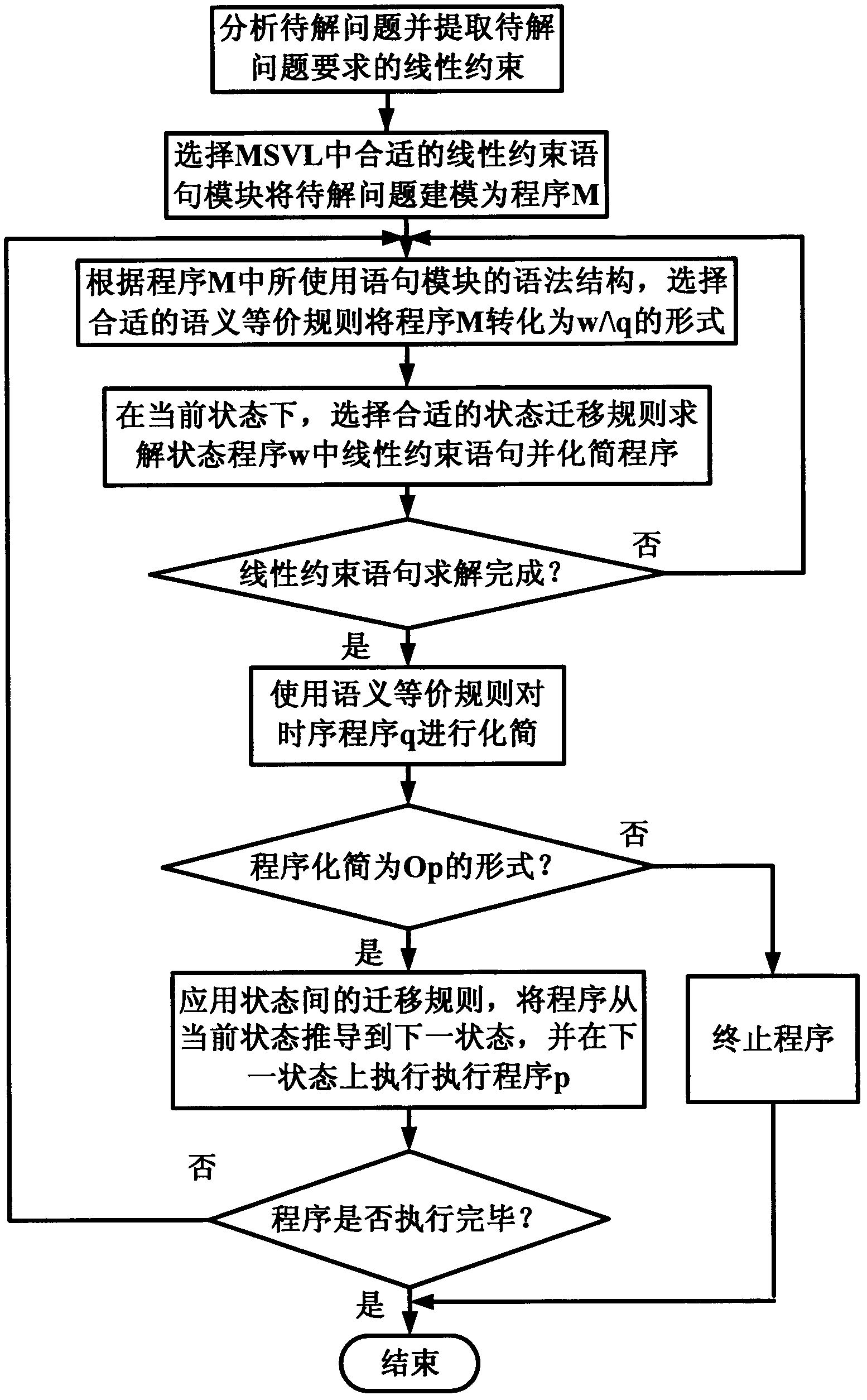
[0101] The present invention is also a method for executing the MSVL linear constraint system. The MSVL linear constraint system in Embodiment 1 is used, and each module in the MSVL linear constraint system is applied in the execution steps. refer to figure 2 , the execution method steps include:
[0102] Step A first analyzes the problem to be solved and extracts the linear constraints required in the problem to be solved. The linear constraint is the main solution aspect of the problem to be solved. Analyzing the problem to be solved and extracting the problem to be solved need to be done manually.
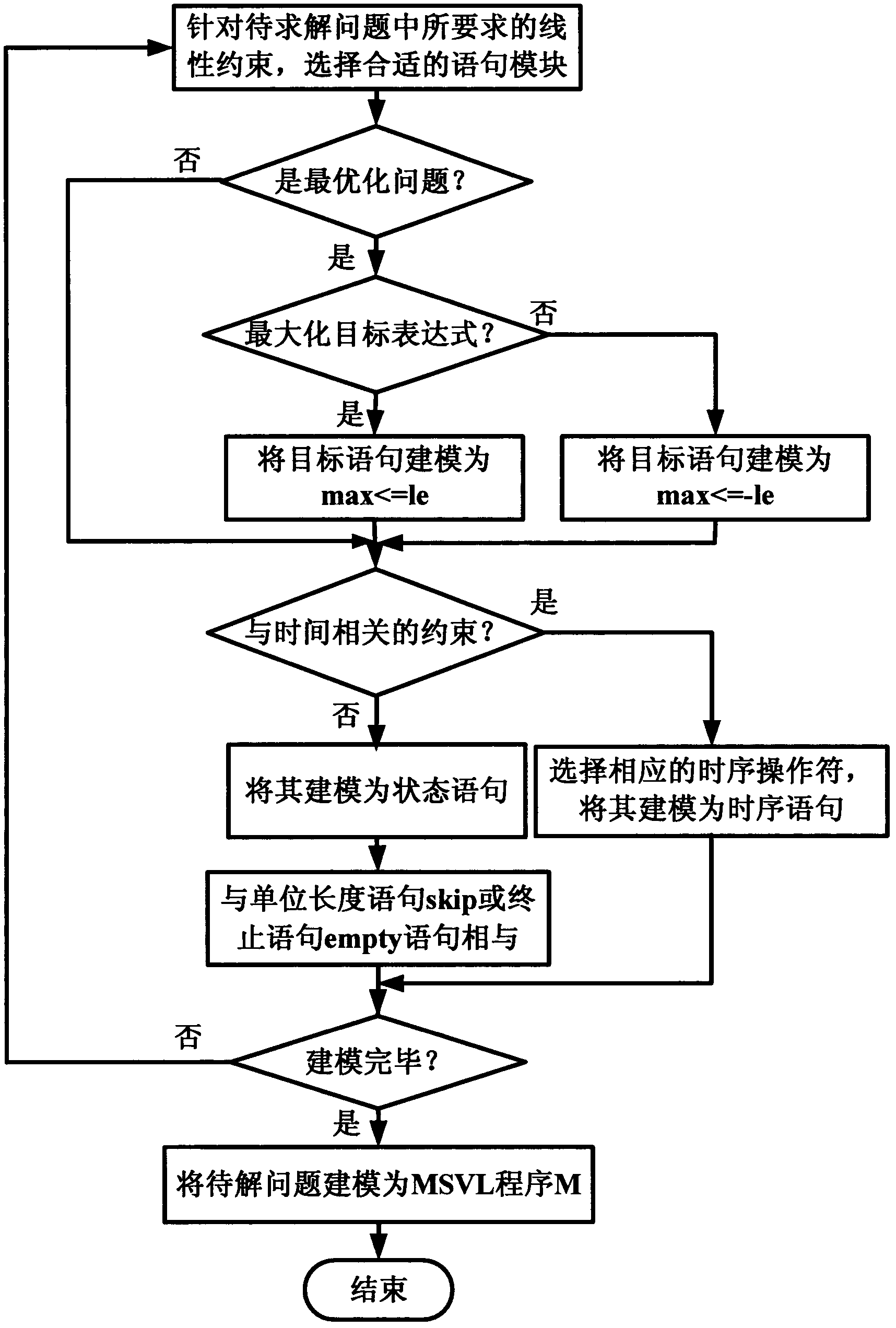
[0103] Step B selects the linear constraint statement module corresponding to the problem to be solved in MSVL, such as linear and other words Non-strict inequality (≥, ≤), etc., and other sentence modules model the problem to be solved as an MSVL program M, that is to say, the problem to be solved is abstracted into an MSVL program that faithfully reflects the behavior of th...
Embodiment 3
[0144] The MSVL linear constraint system is the same as in Embodiment 1, and the execution method of the MSVL linear constraint system is the same as in Embodiment 2. The semantic equivalence rules and state transition rules in the linear constraint solving subsystem involved are described and implemented as follows:
[0145] Semantic equivalence rules: MSVL programs can be converted into equivalent forms through semantic equivalence rules, which lay the foundation for further solving linear constraints.
[0146] Algebraic properties of linear expressions: (where le 1 ,le 2 represents a linear expression, c 1 , c 2 Represents a constant, b represents a static variable whose value remains constant over the entire interval)
[0147] AEqu1: 0+le 1 ≈le 1 AEqu2: (le 1 +le 2 )+le 3 ≈le 1 +(le 2 +le 3 )
[0148] AEqu3:le 1 +le 2 ≈le 2 +le 1 AEqu4: -le 1 ≈le 1
[0149] AEqu5:le 1 +(-le 1 )≈0 AEqu6: -(le 1 +le 2 )≈-le 1 -le 2
[0150]...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com