Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method for infinity point representation under affine coordinate system in elliptic curve cryptosystem

A technology of elliptic curve cryptography and affine coordinate system, which is applied in the field of representation of infinity point in affine coordinate system in elliptic curve cryptography, and can solve the inability of infinity point and the inability of affine coordinate point addition and multiplication process Realization, representation, etc.

Inactive Publication Date: 2011-06-22
SHANGHAI HUAHONG INTEGRATED CIRCUIT
View PDF4 Cites 7 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

But in affine coordinates, since the representation of affine coordinates is (x, y), there is no z component, so the point at infinity cannot be represented in affine coordinates
This will make the point addition and multiplication process involving affine coordinates impossible or incorrectly calculated

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method for infinity point representation under affine coordinate system in elliptic curve cryptosystem
  • Method for infinity point representation under affine coordinate system in elliptic curve cryptosystem

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

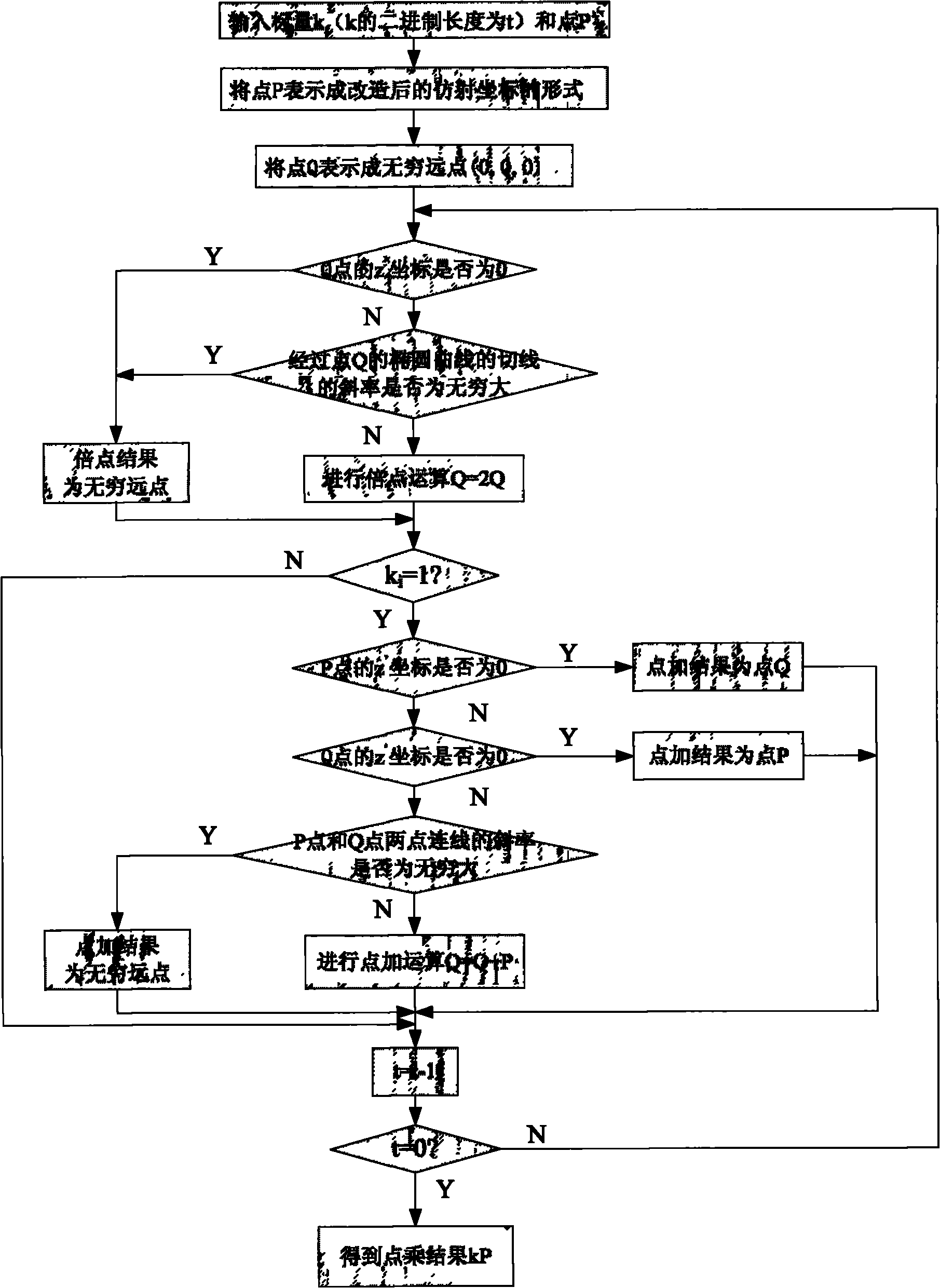
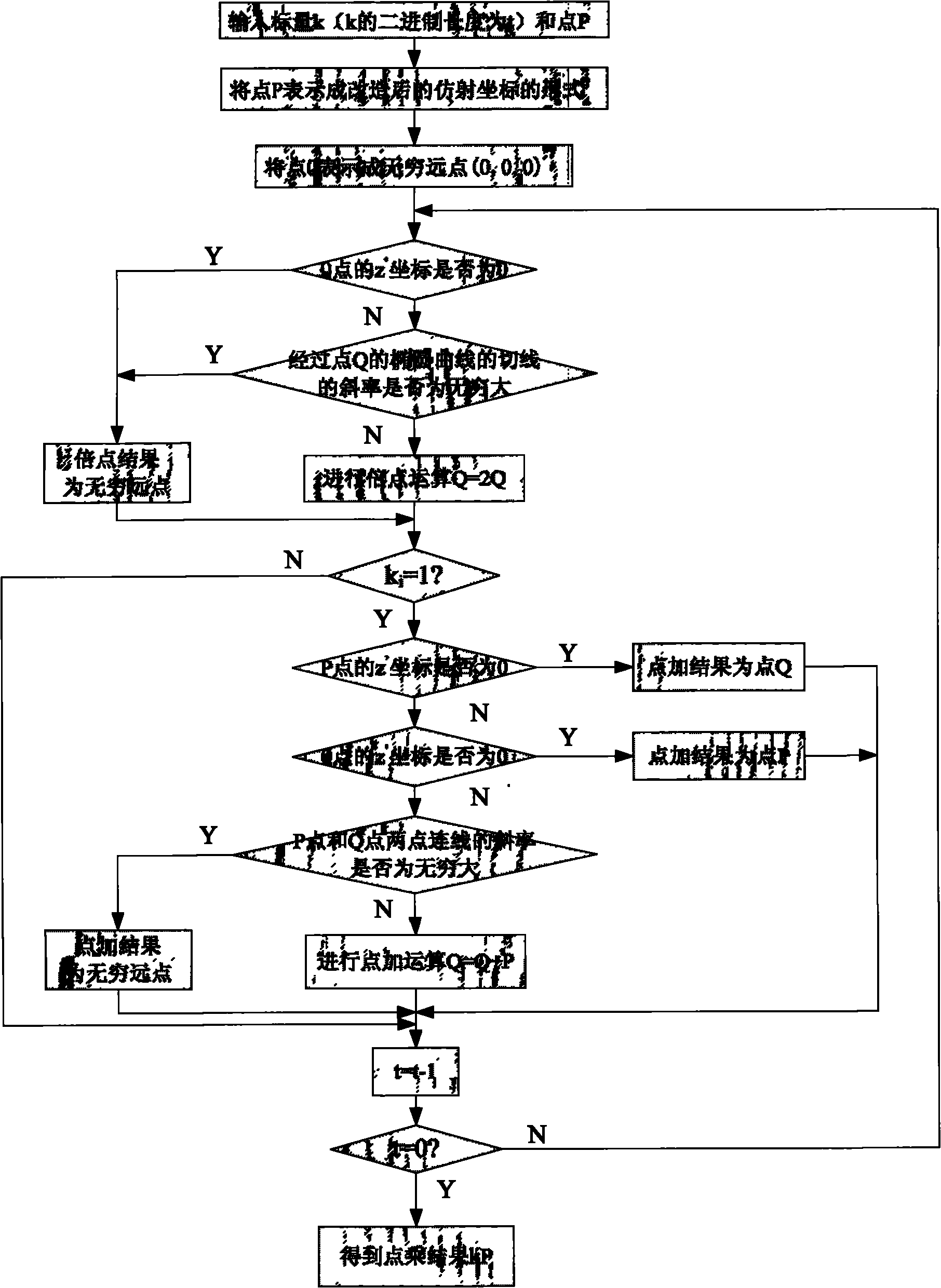
[0021] The existing ordinary affine coordinates only have two components x and y, which cannot represent a point at infinity. Add a component z' to the improved new affine coordinate system, and use this component to distinguish the ordinary point from the infinite point. The z' coordinate of an ordinary point is 1, while the z' coordinate of an infinite point is 0. When adding points or doubling points, judging the z' coordinate of the input point can determine whether the point is an infinite point, and then perform different processing.

[0022] In the process of point multiplication, the generation of infinity points can be divided into two cases:

[0023] 1. Initial variable assignment; generally, before the calculation of the point multiplication main loop, it is necessary to set a certain point as the point at infinity, and then perform the cycle operation of point addition and point multiplication on this point.

[0024] 2. During the operation of dot addition and do...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The present invention discloses a method for infinity point representation under an affine coordinate system in an elliptic curve cryptosystem, including the step of adding a component z' in an existing affine coordinate system having two components, x and y, to form a new affine coordinate system. An ordinary point on an elliptical curve is represented as (x, y, 1) in the new affine coordinate system, i.e., coordinate point z'=1, wherein the ordinary point is represented as (x, y) in the existing affine coordinate system; and an infinity point on the elliptic curve is represented as (0, 0, 0) in the new affine coordinate system, i.e., coordinate point z'=0. The method for infinity point representation under the affine coordinate system in the elliptic curve cryptosystem enables an infinity point originally unable to be represented in the affine coordinate system, to be represented in the improved affine coordinate system, thereby being capable of distinguishing the infinity point from the ordinary point in the affine coordinate system, and enables the point operation of addition and multiplication relating to the affine coordinate system to be correctly realized.

Description

technical field [0001] The invention relates to the field of Elliptic Curve Cryptosystem (ECC, Elliptic Curve Cryptosystem), in particular to a method for expressing a point at infinity in an affine coordinate system in the Elliptic Curve Cryptosystem. Background technique [0002] In 1985, Neil Koblitz, Victor Muller and others applied elliptic curves to cryptography and made a major breakthrough in the research of public key cryptosystems. This is the cryptosystem on elliptic curves - ECC. Its security is built on the difficulty of the Elliptic Curve Discrete Logarithm Problem (ECDLP). The elliptic curve cryptosystem can provide the same function as the RSA cryptosystem, but because of its powerful "short key" advantage, it has become the development direction of the public key cryptosystem. [0003] The main operation of ECC is point multiplication (Scalar Multiplication), which is to calculate kP, where P is a point on the elliptic curve, and k is a positive integer. D...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): H04L9/30
Inventor 柴佳晶
Owner SHANGHAI HUAHONG INTEGRATED CIRCUIT
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com