Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Orthogonalization algorithm for solving satisfiability problem

A satisfying and orthogonal technology, applied in the field of formal verification of VLSI, which can solve the problem of excessively increasing the scale of learning clauses, and achieve the effect of high speed, high efficiency, and speeding up the simplification process.

Inactive Publication Date: 2008-10-29
FUDAN UNIV
View PDF0 Cites 3 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, the DPLL algorithm still has the problem that the size of the learning clause increases too fast, which is inherent in the DPLL algorithm itself, so new algorithms still need to be studied

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Orthogonalization algorithm for solving satisfiability problem
  • Orthogonalization algorithm for solving satisfiability problem
  • Orthogonalization algorithm for solving satisfiability problem

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

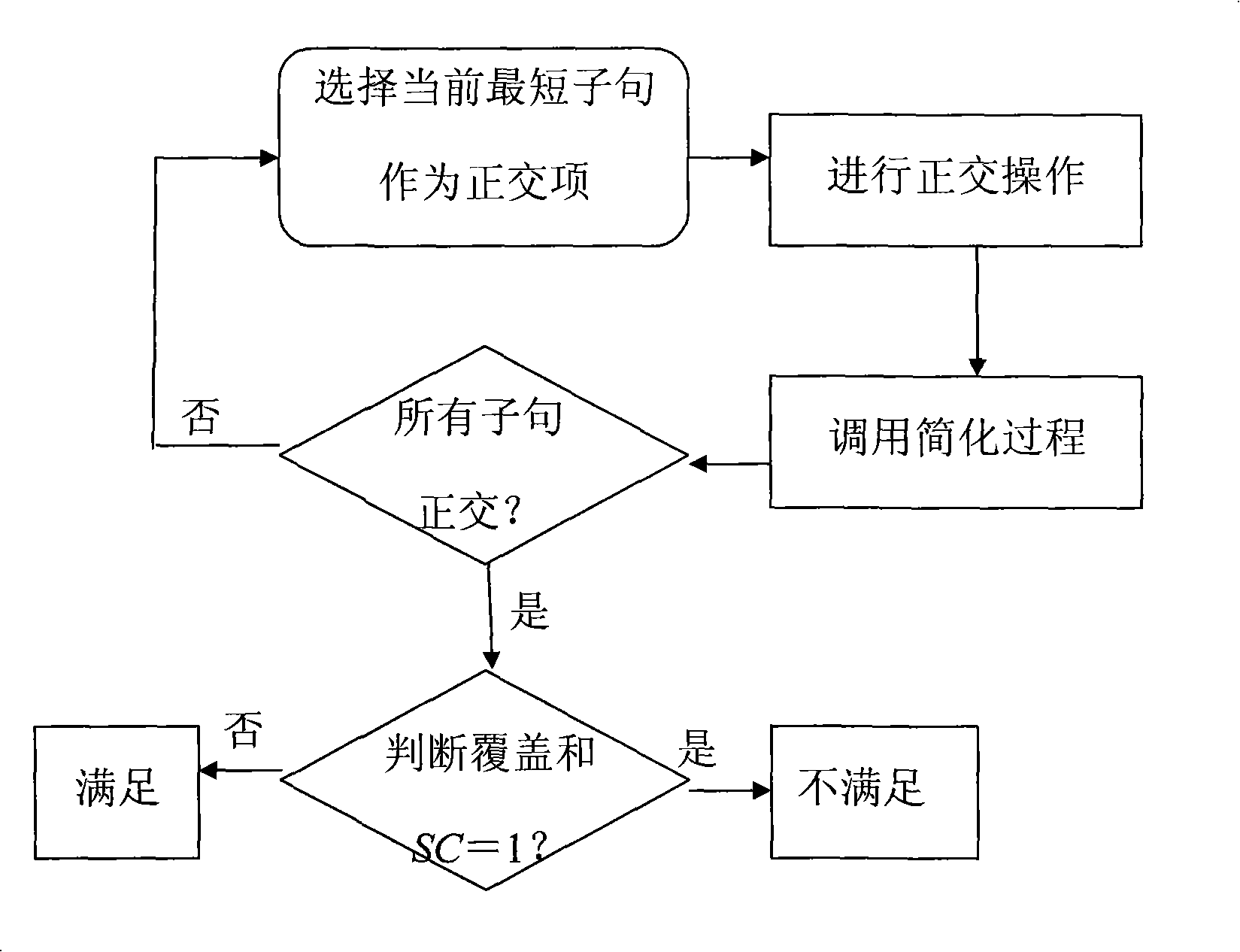
[0043] Combining the clause orthogonalization process and 4 kinds of simplification techniques, the present invention provides a new algorithm utilizing the orthogonal method to solve the SAT problem, and its flow chart is as attached figure 2 shown.

[0044] In order to illustrate the implementation process of the algorithm of the present invention, an example is given below.

[0045] F= (x 1 ∨x 3 ) ∧ (x 1 ∨x 2 ∨x 3 ) ∧ (x 1 ∨x 3 ∨x 4 ) ∧

[0046] (x 1 ∨x 3 ∨x 4 ) ∧ (x 1 ∨x 2 ∨x 3 ∨x 4 ) ∧ (x 3 ∨x 4 ) ∧ (x 3 ∨x 4 )

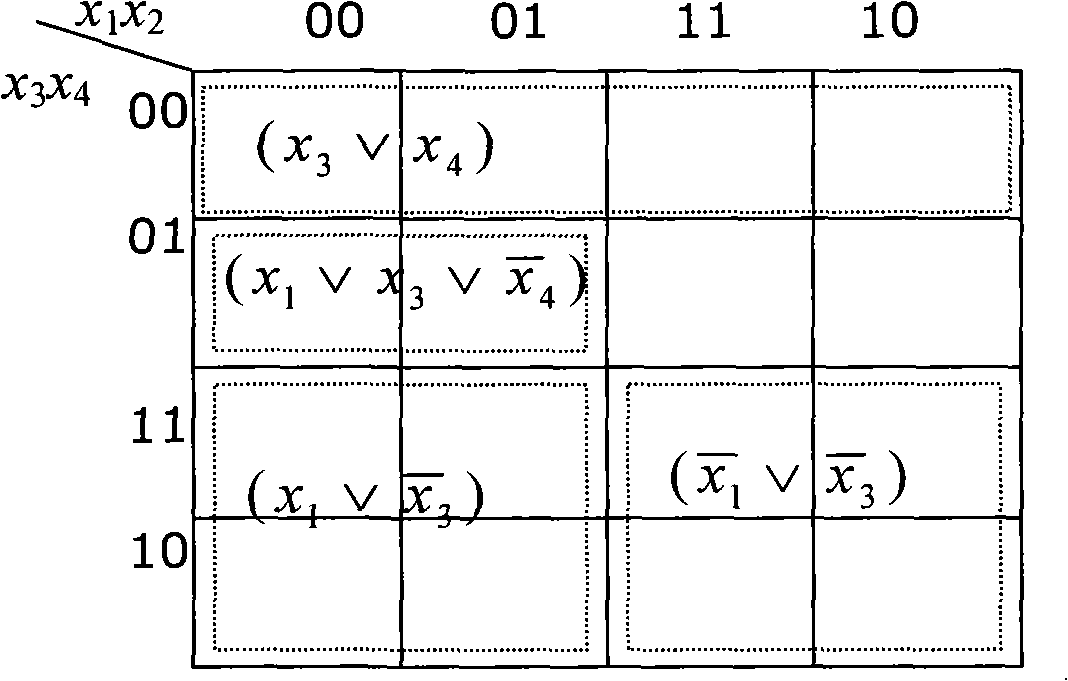
[0047] The SAT question consists of 4 variables and 7 clauses, and the coverage of each clause on the Karnaugh map is as attached image 3 shown. It can be seen that they have many overlapping parts.

[0048] Next, it is orthogonalized using equation (2). First select the shortest clause as an orthogonal item for orthogonal operation. Here the first clause x is selected 1 ∨...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention pertains to the technical field of formal verification of an ultra-large-scale integrated circuit, in particular to an orthogonal algorithm for solving the SAT problem. The algorithm firstly defines an orthogonal relationship among the clauses, then utilizes the features of the orthogonal clauses from the point of eliminating the overlapping information in the clauses, combines the effective simplification technology and gradually simplifies the problem into a group of orthogonal clauses which are fully equivalent to the original problem; finally, whether the SAT is met or not is judged according to the coverage situation on the whole assignment space by the group of the orthogonal clauses. The method of the invention is highly efficient and practical, which can accelerate the simplification process of the problem, improve the calculation speed of solving the problem and be applicable to automatic test vector generation, a timing analysis, logic verification and equivalence verification, etc. during the design of the ultra-large-scale integrated circuit.

Description

technical field [0001] The invention belongs to the technical field of formal verification of ultra-large-scale integrated circuits, and in particular relates to a new method for solving satisfiability problems. technical background [0002] Given a propositional formula, the Boolean satisfiability problem (SAT) determines whether there exists a set of variable assignments that make the formula true. If such an assignment exists, the formula is satisfiable, otherwise the formula is not. Usually satisfiability problems are expressed in conjunctive normal form (CNF). The conjunction paradigm is composed of several clauses "xiangand" (∧), and each clause is composed of several words "xiangand" (∨). The number of words contained in a clause is called the length of the clause. Each literal is either the positive phase (referred to as positive literal) or the reversed phase (referred to as inverse literal) of the variable. For example: (1) formula is a conjunction normal form....

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/50
Inventor 荆明娥赵长虹周电唐璞山
Owner FUDAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com