Eureka AIR delivers breakthrough ideas for toughest innovation challenges, trusted by R&D personnel around the world.

Method and system for quickly generating deep-space small-thrust flying-over orbit

A small thrust and orbital technology, applied in special data processing applications, instruments, electrical digital data processing, etc., can solve problems such as slow calculation speed, large calculation amount, and reduce calculation amount, and achieve the effect of avoiding the global optimization process

Active Publication Date: 2019-12-13
湖南航升卫星科技有限公司
View PDF3 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] The present invention provides a method and system for quickly generating low-thrust flyover orbits in deep space, which are used to overcome the defects of large calculation amount and slow calculation speed in the global optimization low-thrust flyover orbit design method in the prior art, and can realize large-scale task window search, And reduce the amount of calculation, quickly generate overflying orbit

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method and system for quickly generating deep-space small-thrust flying-over orbit
  • Method and system for quickly generating deep-space small-thrust flying-over orbit
  • Method and system for quickly generating deep-space small-thrust flying-over orbit

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

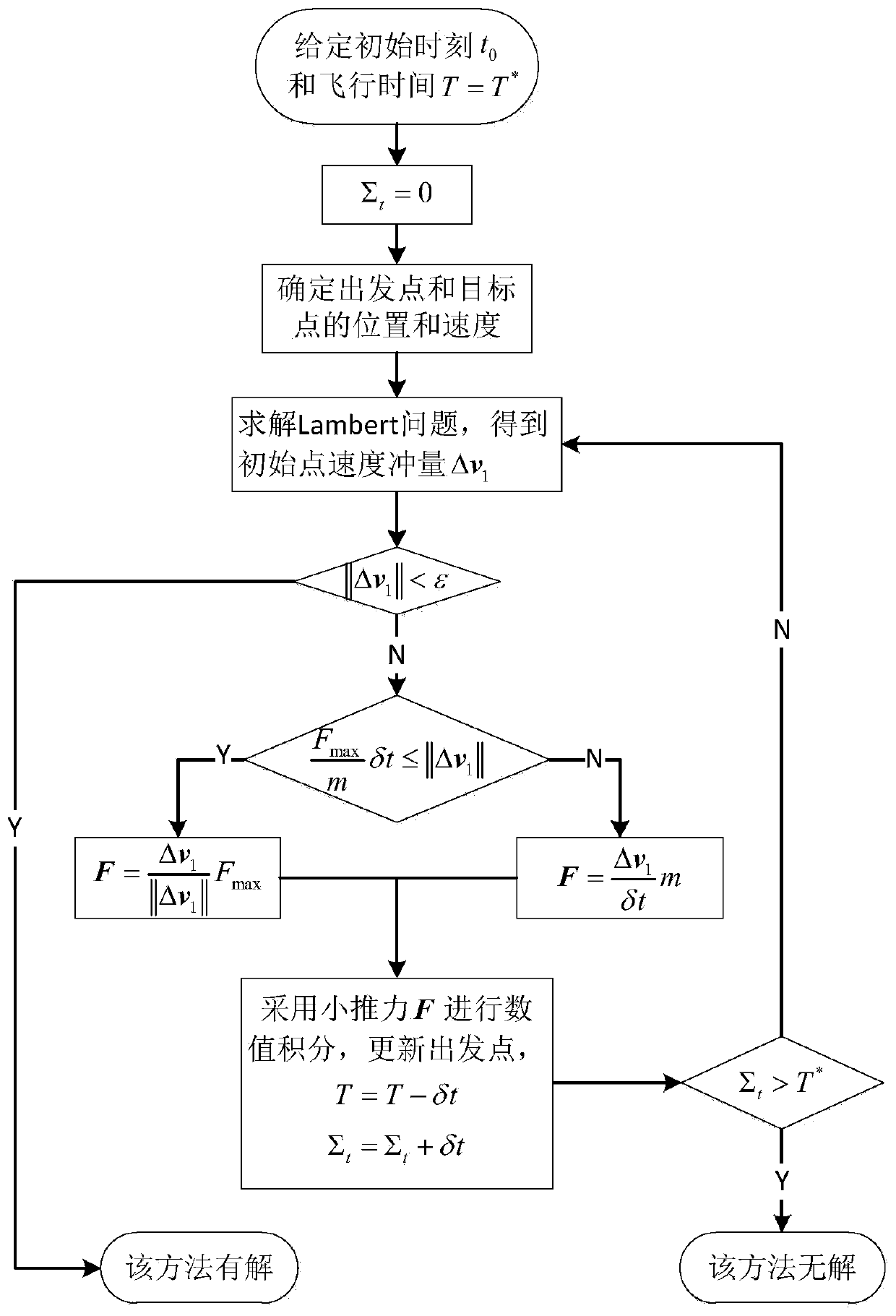
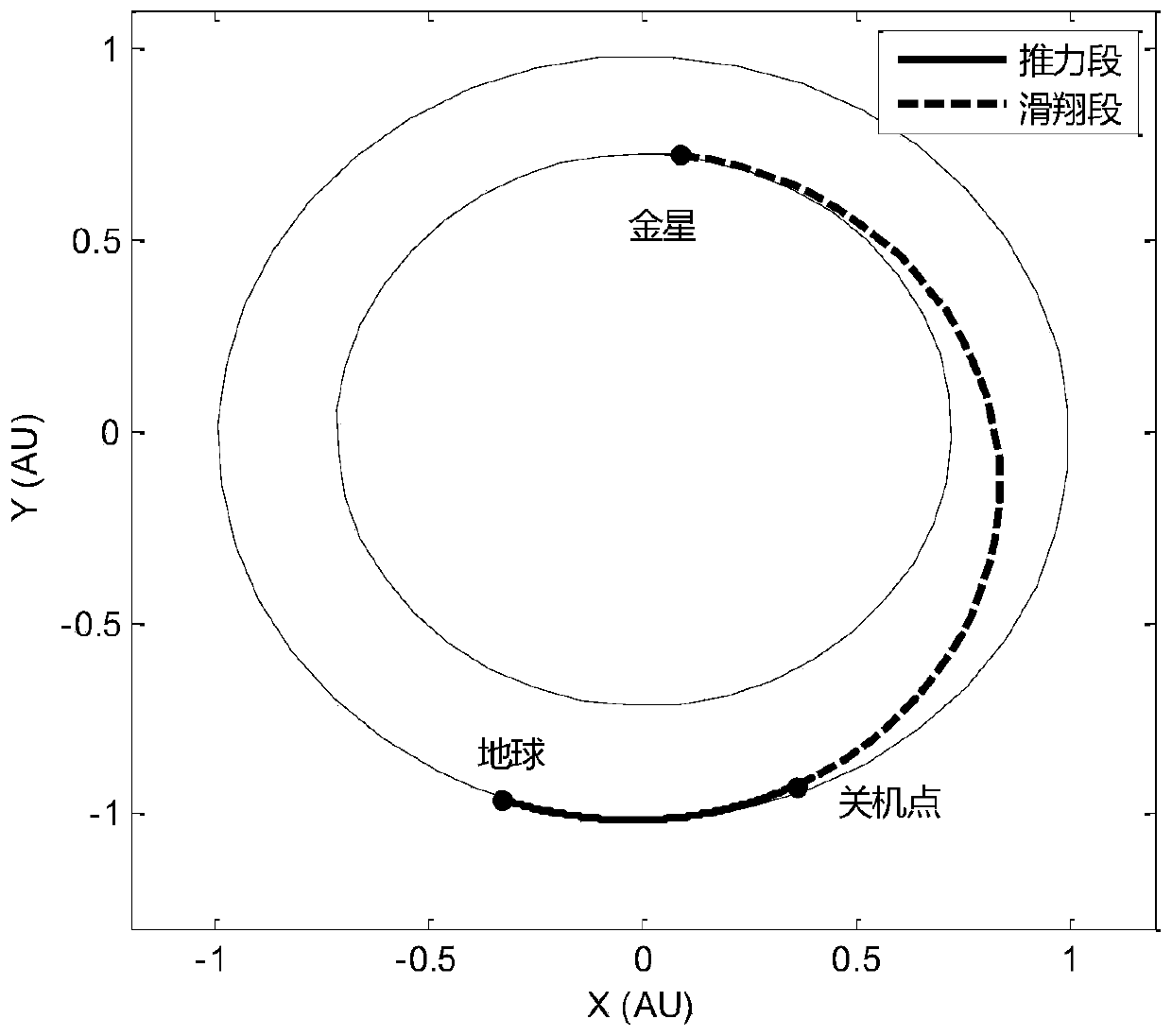
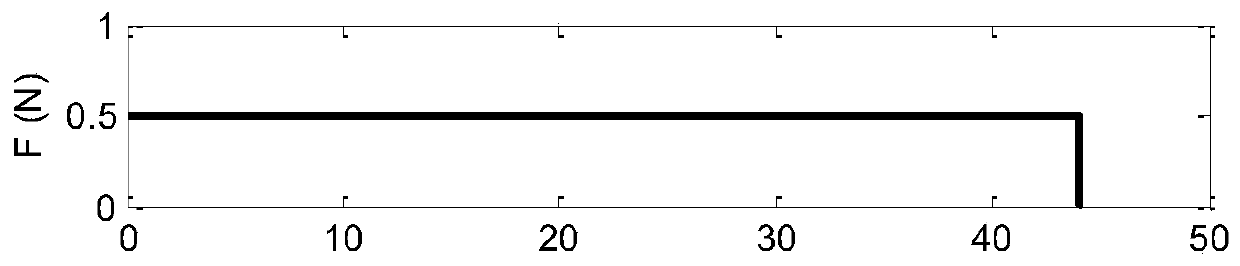
[0027] as attached figure 1 As shown, the embodiment of the present invention provides a method for quickly generating a low-thrust flyover orbit in deep space, including the following steps:

[0028] S1, given starting point position r 0 and the target point position r f and the starting point velocity v 0 , the flight time from the starting point to the target point T=T * , and initialize the current time t 0 and the integrated time variable Σ t ;

[0029] S2, by solving the Lambert problem, the velocity increment Δv is obtained 1 ;

[0030] S301, in the speed increment amplitude ||Δv 1 When || is less than the impulse threshold ε, the speed increment Δv 1 It is transformed into a small thrust vector F; when the above-mentioned speed increment amplitude meets the set impulse threshold ε, it means that the calculation procedure of this scheme has a solution, and the small thrust vector can be obtained according to Newton’s second law, and can be obtained according to...

Embodiment 2

[0036] As a further improvement of Embodiment 1, continue to refer to figure 1 :

[0037] S1, given starting point position r 0 and the target point position r f and the starting point velocity v 0 , the flight time from the starting point to the target point T=T * , and initialize the current time t 0 and the integrated time variable Σ t ;

[0038] S2, by solving the Lambert problem, the velocity increment Δv is obtained 1 ;

[0039] S302, in the speed increment amplitude ||Δv 1 || is greater than or equal to the impulse threshold ε, and satisfies When , output a small thrust vector:

[0040] Among them, F max is the maximum and minimum thrust that the propulsion system can output, m is the mass of the spacecraft, and δt is the integration time;

[0041] S4. Perform a numerical integration of the time length δt on the first-order dynamic equations of the classic two-body orbit of a classic spacecraft under the action of a small thrust vector, and update the sta...

Embodiment 3

[0046] As a further improvement of Embodiment 1, continue to refer to figure 1 :

[0047] S1, given starting point position r 0 and the target point position r f and the starting point velocity v 0 , the flight time from the starting point to the target point T=T * , and initialize the current time t 0 and the integrated time variable Σ t ;

[0048] S2, by solving the Lambert problem, the velocity increment Δv is obtained 1 ;

[0049] S303, in the speed increment amplitude ||Δv 1 ||When greater than or equal to the impulse threshold ε, and not satisfied When , output a small thrust vector:

[0050] Among them, F max is the maximum and minimum thrust that the propulsion system can output, m is the mass of the spacecraft, and δt is the integration time;

[0051] S4. Perform a numerical integration of the time length δt on the first-order dynamic equations of the classic two-body orbit of a classic spacecraft under the action of a small thrust vector, and update th...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method and a system for quickly generating a deep-space small-thrust flying-over orbit, and the method comprises the following steps: 1), giving an initial moment and flighttime, and determining the position speeds of a starting point and a target point; 2) solving a Lambert problem to obtain an initial speed increment; 3) converting the speed increment into a small thrust vector; 4) carrying out numerical integration on the orbit by utilizing a small thrust vector; and 5) updating the starting point position and the flight time, solving the Lambert problem again, and repeating the steps 3), 4) and 5) until the integral time is greater than the given flight time. According to the method, a global optimization process with a huge calculation amount can be avoided,the existence of the low-thrust orbit can be quickly judged, and a given feasible solution can provide a very good initial value for further numerical optimization.

Description

technical field [0001] The invention relates to the technical field of spacecraft track design, in particular to a method and system for quickly generating a low-thrust flyover track in deep space. Background technique [0002] The low-thrust propulsion system has the remarkable characteristics of high specific impulse and low propellant mass consumption, and has unique advantages and good development prospects in the field of deep space exploration. However, small thrust also has the characteristics of small thrust value and continuous action, which brings great challenges to the design of low-thrust orbits. The vast majority of existing literature adopts global optimization methods, which are divided into three categories: indirect methods, direct methods and hybrid methods. The indirect method does not have high requirements for the estimation of the initial value of the orbit, but the calculation amount is very large and the calculation speed is slow; the direct method ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/50
CPCY02T90/00
Inventor 项军华
Owner 湖南航升卫星科技有限公司
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com