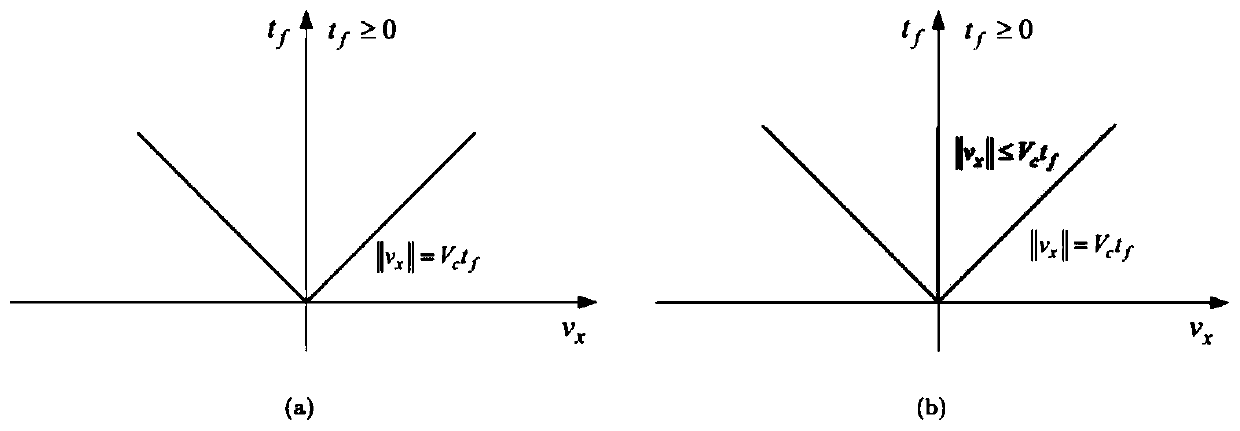Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Time optimal rapid three-dimensional obstacle avoidance path planning method

A time-optimized and path-planning technology, applied in three-dimensional position/channel control, etc., can solve problems such as unguaranteed convergence and solution efficiency, and achieve the effect of improving task response ability and realizing online planning.

Active Publication Date: 2019-05-31
BEIJING INSTITUTE OF TECHNOLOGYGY
View PDF7 Cites 23 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

It is often not feasible to blindly solve this non-convex problem through violent methods (such as nonlinear programming algorithms), because the convergence and solution efficiency of such methods cannot be guaranteed

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Time optimal rapid three-dimensional obstacle avoidance path planning method
  • Time optimal rapid three-dimensional obstacle avoidance path planning method
  • Time optimal rapid three-dimensional obstacle avoidance path planning method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

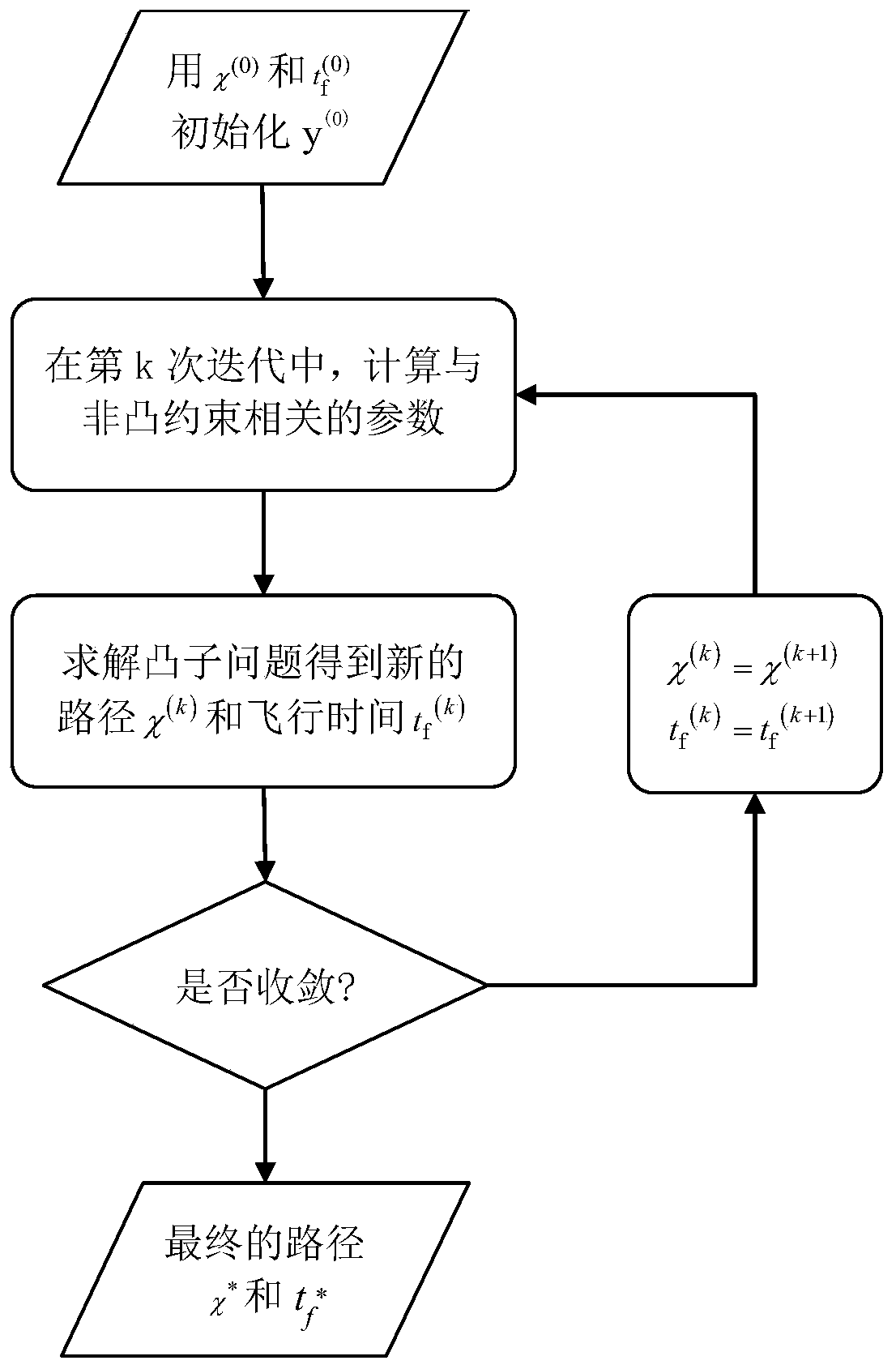
[0154] A method for time-optimal path planning considering obstacle constraints disclosed in this embodiment, the specific steps are as follows:

[0155] Step 1: UAV kinematics modeling. based on figure 1 As shown, the dimensionless motion equation of UAV three-dimensional obstacle avoidance is expressed as:

[0156]

[0157] where [x, y, z] T is the spatial position of the UAV, z is the height, x, y are the coordinates in the orthogonal direction of the horizontal plane; Vc is the speed of the UAV, which is assumed to be a known quantity; ψ and ϕ are the flight path angle and heading angle, respectively. In equation (1), in addition to ψ and φ, the distance variable [x, y, z] T Using the Euclidean distance L of the initial and end positions 0 to normalize, the velocity is V c Normalized. Both time and specific impulse use L 0 / V c Normalized.

[0158] Step 2: Establish an optimal control problem model for obstacle avoidance path planning:

[0159] The control qua...

Embodiment A

[0275] Embodiment A Barrier-free path planning

[0276] For the special two-dimensional case, that is, the Dubins problem with z=0, the initial and end conditions are detailed in Table 1. For convenience, the maximum turning radius is set to 120m (the maximum curvature is 1 / 120), a max =V c *1 / 120=0.83m / s 2 . Convergent solutions are obtained in 3 iterations, and each iteration only takes 0.01-0.02 seconds to solve SOCP problem P3. Since the values ​​z and ψ are always zero (consistent with the numerical solution), they do not show up in the plot for 2D problems.

[0277] Table 1 Initial and terminal conditions of two-dimensional path planning without obstacle avoidance constraints

[0278]

[0279] The calculation convergence process under the Dubins task is as follows Figure 6 and Figure 7 . It can be seen that after the second iteration, the continuous solution of the path and flight time has little difference in the scale of the figure, and the error between e...

Embodiment B

[0283] Embodiment B Three-dimensional path planning considering obstacles

[0284] In this case, set up a path planning task with two obstacle avoidance constraints. As a comparison, this case also gives the solution without obstacle avoidance constraints under the same endpoint conditions and overload constraints. The maximum acceleration is set to 0.8m / s 2 , the initial and termination conditions are shown in Table 3. The radius of the obstacle ball is 80m, centered at [250, 220, 280]m, the radius of the obstacle cylinder is 60m, and its center line passes through the x-y plane at [100, 150, 0]m with and without avoidance. obstacle limit, the minimum flight time is 71.41 seconds and 70.34 seconds respectively. Figure 11-17 The converged solution plotted in shows that the initial, terminal, and acceleration constraints are all satisfied. Figure 11 The optimal paths with and without obstacle avoidance constraints are plotted in . exist Figure 12 In , the top represent...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a time optimal rapid three-dimensional obstacle avoidance path planning method, particularly relates to an unmanned aerial vehicle obstacle avoidance path planning method, andbelongs to the field of unmanned aerial vehicle path planning. According to the invention, the method comprises the steps: establishing an unmanned optimal control model which takes the acceleration in each direction as a control variable and contains the flight time sum through considering the maximum acceleration and obstacle constraint conditions; loosening an original non-convex nonlinear optimization problem into a second-order cone programming problem; and finally, solving a series of second-order cone programming problems through iteration to obtain a solution of an original problem andobtain an optimal change strategy in the speed direction. In other words, the obstacle avoidance path planning with the optimal time is realized by coordinating the flight time and the flight speed direction, the online planning of the obstacle avoidance path and the related control quantity can be realized, and the task response capability of the unmanned aerial vehicle can be further improved through the optimized flight path with the optimal time.

Description

technical field [0001] The invention belongs to the field of unmanned aerial vehicle path planning, and in particular relates to an obstacle avoidance path planning method for an unmanned aerial vehicle, in particular to a time-optimal fast three-dimensional obstacle avoidance path planning method based on online convex optimization. Background technique [0002] In the past few years, UAV technology has penetrated into all aspects of production and life, and path planning plays a key role in UAV monitoring, payload delivery, agricultural plant protection, target search and other tasks. [0003] The time-optimal path planning problem is a typical optimization problem. In order to improve the flexibility and rapidity of UAV missions, it is necessary to solve the corresponding optimal control model in real time to obtain the flight path with the least time consumption. It is often not feasible to blindly solve this non-convex problem through violent methods (such as nonlinear ...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G05D1/10
Inventor 姜欢刘新福
Owner BEIJING INSTITUTE OF TECHNOLOGYGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com