Spectral unmixing scheme based on abundance sparse and endmember orthogonal constraint NMF(Non-negative Matrix Factorization)
An orthogonality and sparsity technology, applied in the field of hyperspectral remote sensing image unmixing, which can solve the problem of easily falling into local extreme values, and achieve the effect of ensuring independence.
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
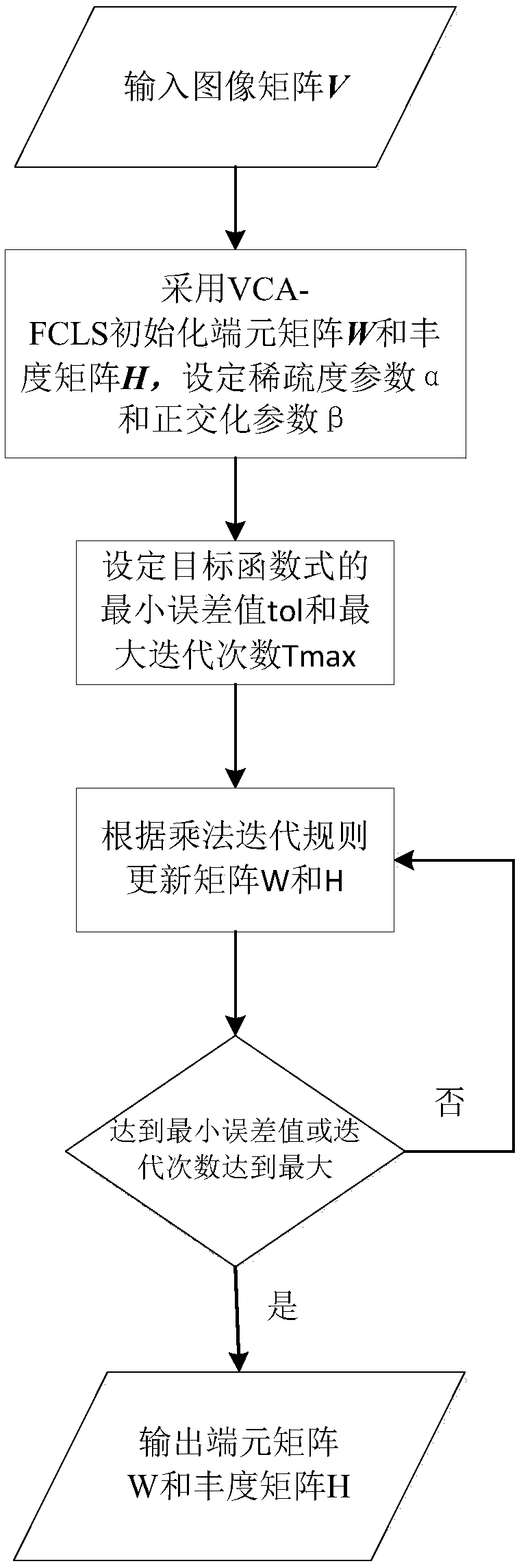
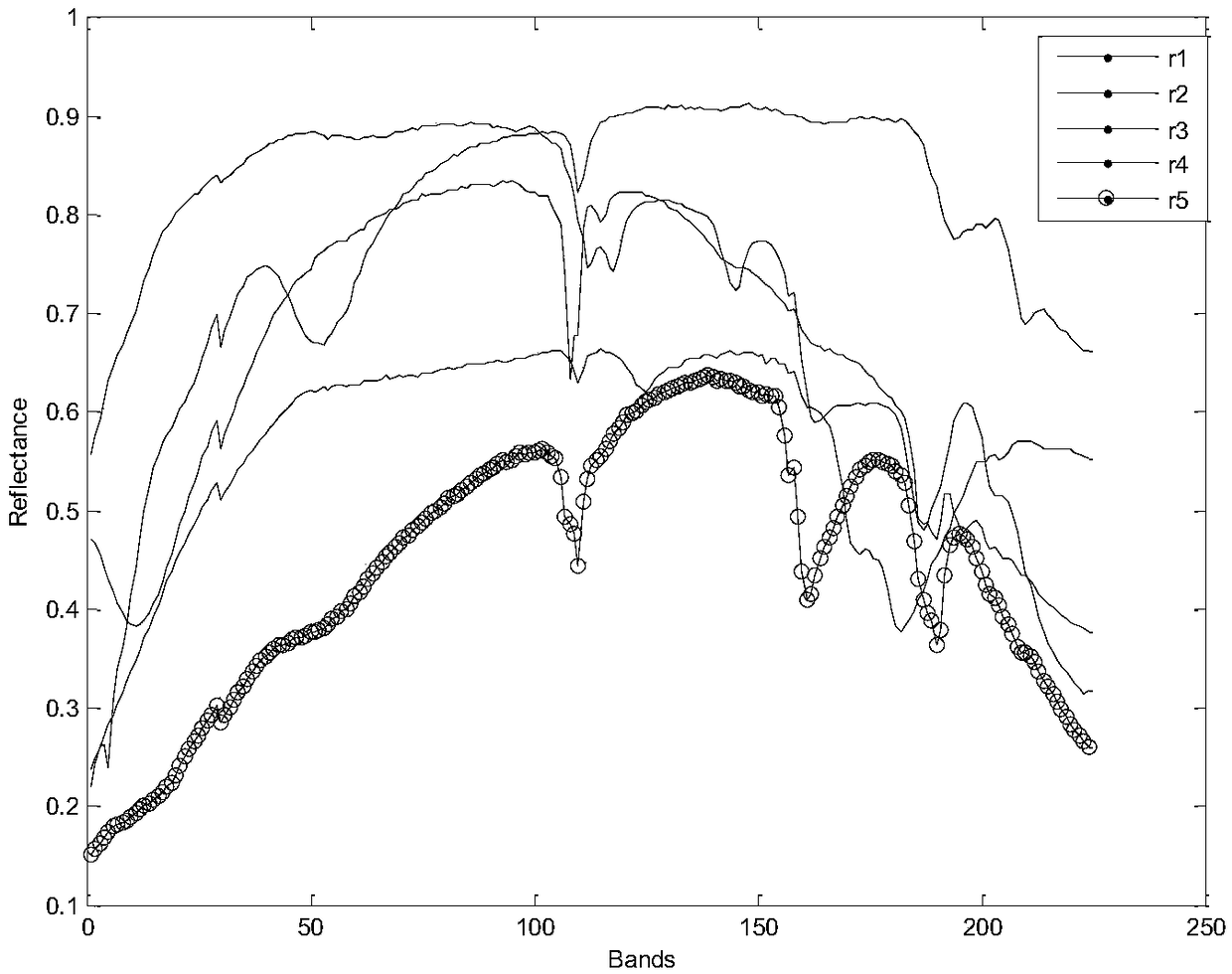
[0029] A hyperspectral image unmixing method based on the orthogonality of endmembers and abundance sparsity constrained NMF, according to the linear spectral mixing model R=EA+N in step 1, R=[r i ,...,r n ]∈R d×n Represents the n pixels and d bands of the hyperspectral image, the end member spectrum matrix E=[e 1 ,e 2 ,...,E p ], the end member spectrum matrix E contains p end member vectors, and the end member abundance matrix A=[a 1 ,a 2 ,...A n ] T , Each component in the abundance matrix A represents the abundance of the corresponding end-member, and abundance refers to the proportion of an end-member in the pixel, which satisfies the conditions of "sum is one" and "non-negative"
[0030]
[0031] 3. Step 2: Perform constrained NMF based on the orthogonality of endmembers and abundance sparsity: use the NMF algorithm to establish an objective function based on the Euclidean distance based on the linear spectral mixing model
[0032]
[0033] among them Represents the Frobenius...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com