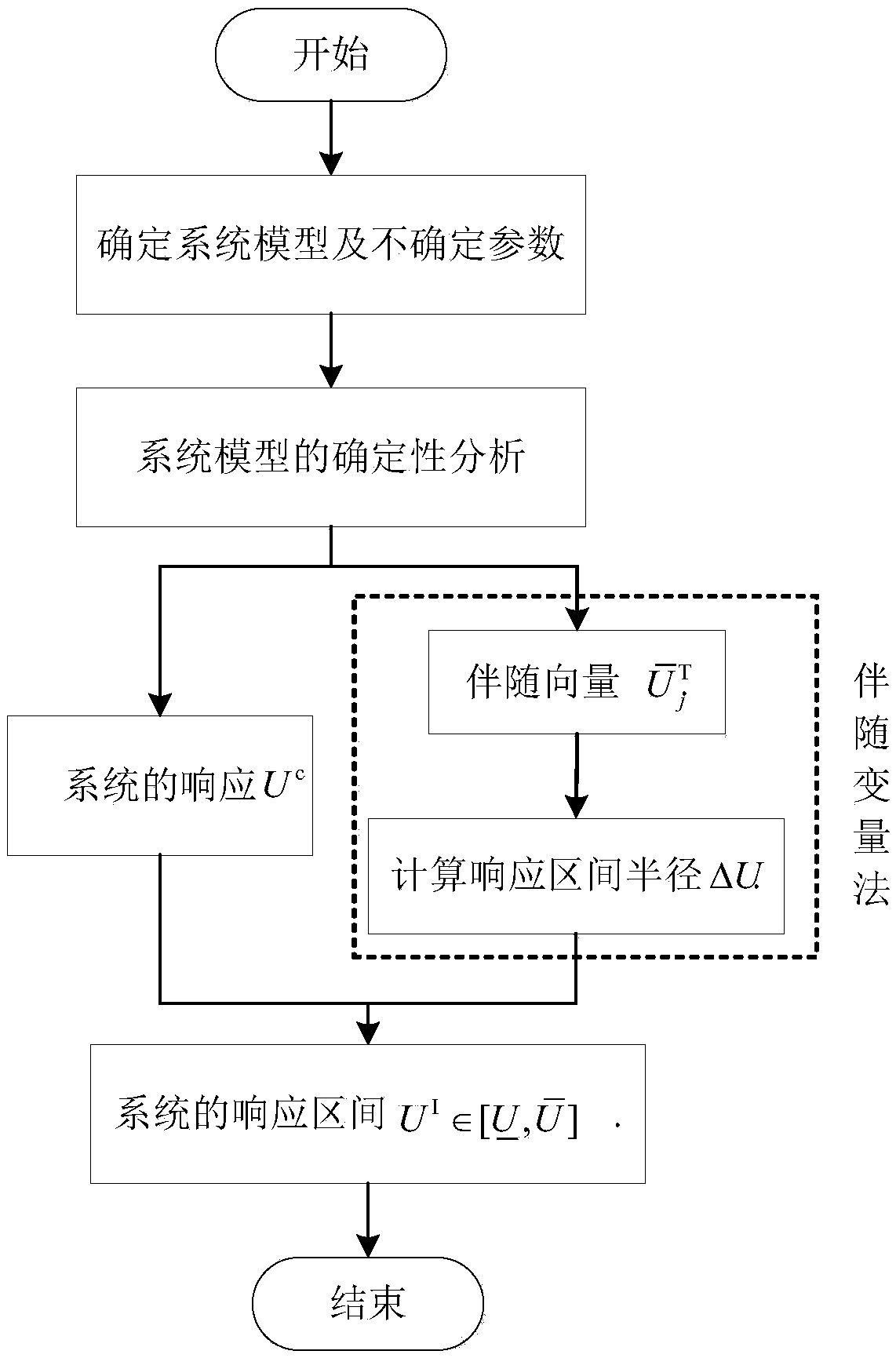
Structural interval response propagation analysis method with multiple uncertain parameters based on adjoint variable method
A technology for determining parameters and accompanying variables. It is used in special data processing applications, electrical digital data processing, instruments, etc. It can solve the problems of affecting the derivation accuracy, increasing the calculation cost of the difference method, and not having display expressions, so as to improve the calculation efficiency. Efficiency, increased computation, and the effect of efficient response boundaries
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment
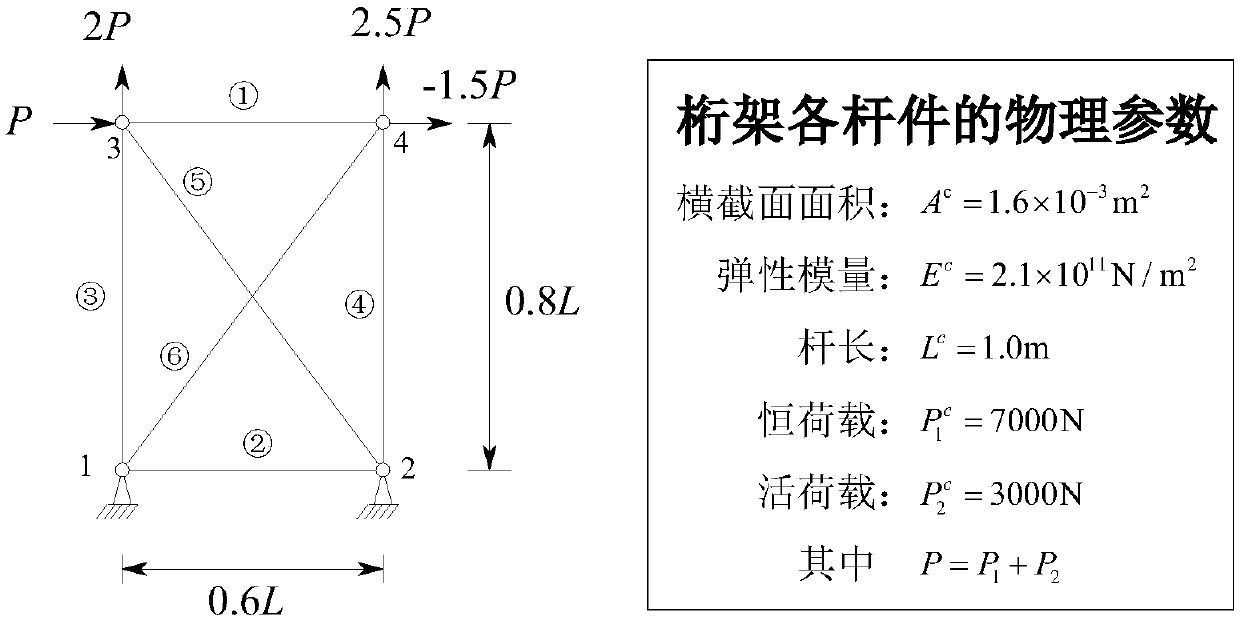
[0077] In order to fully understand the characteristics of the present invention and its applicability to engineering practice, the present invention establishes as figure 2 The shown six-bar truss structure contains uncertain parameters such as elastic modulus, member cross-sectional area and load, and the structural displacement propagation is analyzed. The truss structure and related physical parameters such as figure 2 As shown, in order to fully consider the influence of uncertainty parameters on structural displacement and consider the symmetry of the structure, the uncertainty parameters are introduced as follows: the elastic modulus of rod ①②, the cross-sectional area is E 1 and A 1 ; The modulus of elasticity of the rod ③ ④, the cross-sectional area is E 2 and A 2 ; The modulus of elasticity of the rod ⑤ ⑥, the cross-sectional area is E 3 and A 3 . The loads on the structure are asymmetrical loads, and the four loads are F 1 , F 2 , F 3 and F 4 . Therefor...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D Engineer
- R&D Manager
- IP Professional
- Industry Leading Data Capabilities
- Powerful AI technology
- Patent DNA Extraction
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com