Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Elastic modulus test method based on virtual pure bending material

A technology of elastic modulus and testing method, which is applied in the field of elastic modulus testing based on virtual pure bending materials, can solve problems such as the inability to achieve modulus measurement, achieve short test time, long time-consuming, and avoid tediousness Effect

Active Publication Date: 2019-07-23
SHAOXING UNIVERSITY
View PDF5 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

This test method is a static test, which has standard restrictions on the cross-sectional shape and size of the component, and can only be carried out in the laboratory. Moreover, due to the influence of size effects, the elastic modulus measured in the laboratory and the actual component There may be some differences in the true elastic modulus. In addition, for components that have been in service for a long time, their elastic modulus will have a greater change than the original state. If you want to obtain the true elastic modulus of these components that have been in service for a long time, you need new measurement method
And existing known method can not realize the measurement of above-mentioned modulus

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Elastic modulus test method based on virtual pure bending material
  • Elastic modulus test method based on virtual pure bending material
  • Elastic modulus test method based on virtual pure bending material

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

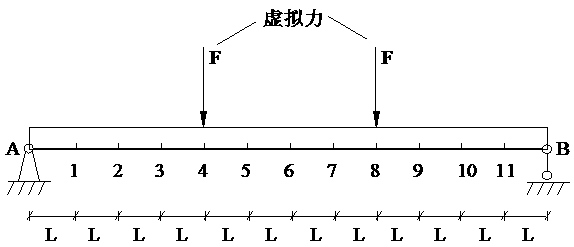
[0029] Example 1: simply supported beam member

[0030] combine figure 1 For the slender simply supported beam member shown, the procedure for measuring the elastic modulus of the material is as follows:

[0031] (1) Install 11 sensors at equal intervals at the bottom of the beam member, conduct a free vibration modal test, and obtain the first m-order modal parameters of the free vibration of the member, that is, the circular frequency ω j and mode shape φ j , the approximate flexibility matrix F of the component is calculated from the obtained data using the formula (1), and the calculation formula of the approximate flexibility matrix F of the component is:

[0032] (2) Construct the corresponding virtual force vector l according to the support constraints of the component v ,for figure 1 For the simply supported beam member shown, for the section between nodes 4 and 8, the constructed virtual force vector is l v =[0,0,0,F,0,0,0,F,0,0,0] T , that is, a virtual conce...

Embodiment 2

[0035] Example 2: Cantilever beam member

[0036] combine figure 2 For the slender cantilever beam member shown, the procedure for measuring the elastic modulus of the material is as follows:

[0037] (1) Install 12 sensors at equal intervals at the bottom of the beam member, conduct a free vibration modal test, and obtain the first m-order modal parameters of the free vibration of the member, that is, the circular frequency ω j and mode shape φ j , the approximate flexibility matrix F of the component is calculated from the obtained data using the formula (1), that is, the calculation formula of the approximate flexibility matrix F of the component is:

[0038] (2) Construct the corresponding virtual force vector l according to the support constraints of the component v ,for figure 2 For the straight-bar cantilever beam member of constant section shown, for the section between nodes A and 8, the constructed virtual force vector is lv =[0,0,0,0,0,0,0,F,0,0,0,-F] T , t...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an elasticity modulus testing method based on a virtual pure bent material, and belongs to the technical field f test or analysis of materials by applying stable tension or pressure to test physical or chemical shapes such as strength character of the solid material. A long and thin component made of the material is used for carrying out a free vibration mode test, a corresponding virtual force vector is constructed according to support constraint conditions of components, a flexibility matrix of the component and the virtual force vector are multiplied to obtain a displacement parameter under a virtual pure bent state, then the curvature of the virtual pure bent section is calculated, and finally, the equation is listed according to balance conditions of the crosssection of the virtual pure bent section to obtain elasticity modulus. The elasticity modulus testing method based on the virtual pure bent material is applied to existing components which have various support constraint conditions and cross section types and have been used for a long time, and has the advantages of simplicity in operation, short time required for test, zero damage, zero limitation to an operation environment and the like.

Description

technical field [0001] The application relates to a method for testing elastic modulus based on virtual pure bending materials, which belongs to the technical field of testing or analyzing materials by applying stable tension or pressure to test physical or chemical shapes such as strength properties of solid materials. Background technique [0002] The elastic modulus of a material is one of its basic mechanical parameters, and the rapid and accurate measurement of the elastic modulus of a material is of great significance for engineering design. Most of the current methods for measuring elastic modulus use uniaxial compression or tensile deformation tests to obtain the compressive elastic modulus and tensile elastic modulus of materials. This test method is a static test, which has standard restrictions on the cross-sectional shape and size of the component, and can only be carried out in the laboratory. Moreover, due to the influence of size effects, the elastic modulus m...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G01M5/00
CPCG01M5/005G01M5/0066
Inventor 杨秋伟王伟李娜
Owner SHAOXING UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com