Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Method of constructing cigarette cut tobacco quality evaluation model based on analytic hierarchy process (AHP)

An analytic hierarchy process and quality evaluation technology, applied in the field of cigarette shredded quality evaluation model construction based on analytic hierarchy process, can solve the problems of insufficient objective and accurate evaluation, inability to effectively promote shredded quality level, and single evaluation index setting

Inactive Publication Date: 2018-01-09
CHINA TOBACCO YUNNAN IND
View PDF0 Cites 20 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Subjective evaluation methods generally use expert experience to judge, and the evaluation results are easily affected by the experience, level and human subjective factors of experts. The evaluation is not objective and accurate enough, and the evaluation index setting is relatively simple.
The qualification rate evaluation method refers to the method of judging whether the shredded tobacco production is qualified according to the production technology requirements through the detection of quality index values. Although the collection and processing of data are simple and clear, this evaluation method cannot accurately indicate the level of physical quality and cannot effectively Promote the improvement of the quality level of silk production

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Method of constructing cigarette cut tobacco quality evaluation model based on analytic hierarchy process (AHP)
  • Method of constructing cigarette cut tobacco quality evaluation model based on analytic hierarchy process (AHP)
  • Method of constructing cigarette cut tobacco quality evaluation model based on analytic hierarchy process (AHP)

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0184] Embodiment 1 Calculate the weight of each evaluation index

[0185] S1: Determine the silk quality evaluation index, build the evaluation index hierarchical structure model, and form an evaluation index system composed of the target layer, the criterion layer and the index layer, such as figure 2 shown;

[0186] S2: According to the relative importance of the evaluation index, establish a relative importance judgment matrix, and calculate the weight of each evaluation index;

[0187] Step S2 specifically includes:

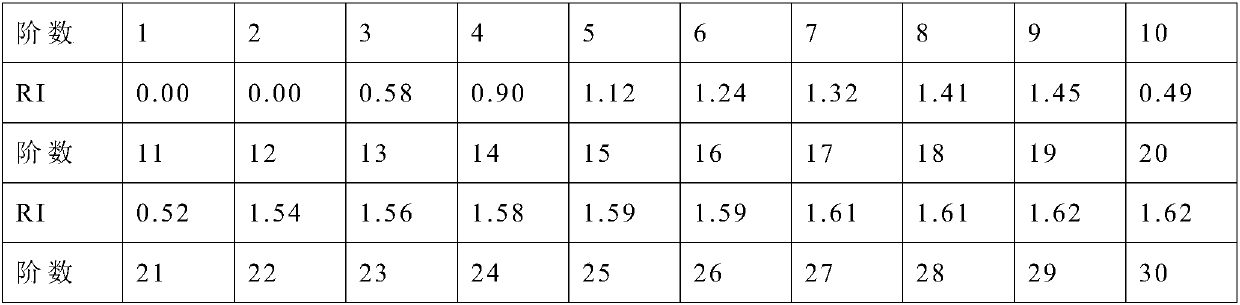
[0188] S21: Use the AHP to quantify the relative importance scale of the abstract indicators into 9 scales of 1-9;

[0189] The so-called 1-9 scale method reflects the relative importance of the two evaluation indicators. The specific principle is: the comparison score of the evaluation index i relative to the evaluation index j is a. ij , then the comparison score of evaluation index j relative to evaluation index i is: a ji =1 / a ij .

[0190] Table ...

Embodiment 2

[0232] Example 2 Calculation of discrete evaluation index variable scores

[0233] S31: The discrete evaluation index variables are divided into large and small variables, which are characterized by the degree of change between the actual measured value and the set value; the quantitative representation of the discrete evaluation index variable is calculated as follows:

[0234] "+" is the evaluation index of Wangliang, "-" is the evaluation index of Wangda, Z x is the degree of change between the measured value of the non-steady-state discrete evaluation index variable and the set value of the index; x pv Set the value for the evaluation index variable or take the value under normal circumstances; x best is the expected optimal value of the evaluation index variable; x is the measured value of the evaluation index;

[0235] (1) Wangda evaluation index—the criterion layer evaluation index and the index layer cumulative cut tobacco weight index included in flavoring

[023...

Embodiment 3

[0248] Embodiment 3 Calculate continuous evaluation index variable score

[0249] S31: Evaluation index variables are divided into discrete evaluation index variables and continuous evaluation index variables; continuous evaluation index variables are characterized by deviation and dispersion;

[0250] The formula for calculating the deviation degree Z of the continuous evaluation index variable is:

[0251] Z is the deviation of the index to be evaluated; μ is the actual mean value of the index to be evaluated; σ Spec Design standard deviation for the indicators to be evaluated;

[0252] The calculation formula of the dispersion degree ρ of the continuous evaluation index variable is:

[0253] ρ is the dispersion of the index to be evaluated; σ Measured is the standard deviation of the actual control of the index to be evaluated; σ Spec Design standard deviation for the index variable to be evaluated;

[0254] Data collection was carried out on the instantaneous frag...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a method for constructing a cigarette cut tobacco quality evaluation model based on the analytic hierarchy process (AHP), and belongs to the technical field of cigarette technology evaluation. The method comprises the steps of firstly, determining cut tobacco quality evaluation indexes, constructing an evaluation index hierarchical structure model, and forming an evaluationindex system composed of a target layer, a criterion layer and an index layer; secondly, establishing a relative importance judgment matrix according to the relative importance of the evaluation indexes and the inter-layer structure relationship, and calculating the weight of each evaluation index by an AHP judgment matrix; thirdly, adopting different calculation methods for different types of index scores; and fourthly, constructing a cigarette cut tobacco quality evaluation model by using a statistical weighting method to make a comprehensive evaluation of the cut tobacco quality. Comparedwith the prior art, the method of the invention establishes a cigarette cut tobacco quality evaluation model based on the AHP, and can trace the causes of the cut tobacco quality and overcome the shortcomings that evaluation results are easily influenced by the experts' experience, level and subjective factors. The evaluation results are more scientific.

Description

technical field [0001] The invention belongs to the technical field of cigarette process evaluation, and in particular relates to a method for constructing a cigarette shred quality evaluation model based on the analytic hierarchy process. Background technique [0002] Analytic hierarchy process (AHP) is a multi-criteria decision-making method that combines qualitative and quantitative analysis proposed by the famous American operations researcher T.L.Satty et al. in the 1970s. The characteristic of this method is that after in-depth analysis of the essence, influencing factors and internal relations of complex decision-making problems, a hierarchical structure model is constructed, and then the thinking process of decision-making is mathematicized by using less quantitative information, so as to provide It provides a simple decision-making method for solving complex decision-making problems with multi-objective, multi-criteria or unstructured characteristics. Its main idea...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06Q10/06G06Q50/04
CPCY02P90/30
Inventor 张超杨双艳李善莲易斌李雯琦龚荣岗冯伟博端凯
Owner CHINA TOBACCO YUNNAN IND
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com