Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Reduced-order kernel function-based high-order polynomial phase signal parameter estimation method

A high-order polynomial and phase signal technology, applied in the direction of electrical digital data processing, calculation, complex mathematical operations, etc., can solve the problem of low estimation accuracy, achieve the effects of reducing nonlinearity, reducing complexity, and eliminating high estimation thresholds

Active Publication Date: 2017-08-22
XIDIAN UNIV
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] The purpose of the present invention is to overcome the above-mentioned defects in the prior art, and propose a high-order polynomial phase signal parameter estimation method based on a reduced-order kernel function, which is used to solve the existing high-order polynomial phase signal parameter estimation method. Technical issues with low precision

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Reduced-order kernel function-based high-order polynomial phase signal parameter estimation method
  • Reduced-order kernel function-based high-order polynomial phase signal parameter estimation method
  • Reduced-order kernel function-based high-order polynomial phase signal parameter estimation method

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

[0032] The present invention will be described in further detail below in conjunction with the accompanying drawings and specific embodiments.

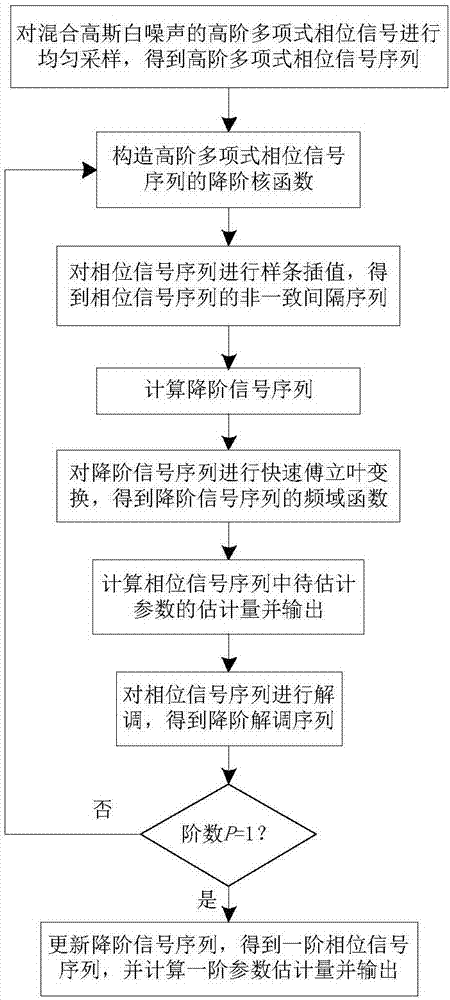
[0033] refer to figure 1 , a high-order polynomial phase signal parameter estimation method based on a reduced-order kernel function, including the following steps:

[0034] Step 1. Uniformly sample the high-order polynomial phase signal x(t) of mixed Gaussian white noise to obtain the high-order polynomial phase signal sequence x(n):

[0035]

[0036] Among them, n is the discrete time variable of the phase signal sequence x(n), w(n) is the Gaussian white noise sequence, Δ is the sampling interval of the phase signal x(t), A 0 is the magnitude of the phase signal x(t), a 1 ,...,a r ,...,a P is the phase parameter to be estimated corresponding to the order r, and P=8 is the highest order number of the phase signal sequence x(n);

[0037] Step 2, use the highest order P of the high-order polynomial phase signal sequence x(n) to...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a reduced-order kernel function-based high-order polynomial phase signal parameter estimation method, and aims at solving the technical problem that the existing high-order polynomial phase signal parameter estimation method is low in estimation precision. The method is realized through the following steps of: uniformly sampling white Gaussian noise-mixed high-order polynomial phase signals to obtain a phase signal sequence; constructing a reduced-order kernel function of the phase signal sequence; carrying out spline interpolation on the phase signal sequence to obtain a non-uniform interval sequence; calculating a reduced-order signal sequence; carrying out fast Fourier transform on the reduced-order signal sequence; calculating estimators of to-be-estimated parameters in the phase signal sequence and outputting the estimators; demodulating the phase signal sequence to obtain a reduced-order demodulated sequence; updating the phase signal sequence, circularly constructing the reduced-order kernel function, calculating estimators of the to-be-estimated parameters in the updated phase signal sequence in sequence and outputting the estimators; and updating the reduced-order signal sequence to obtain a first-order phase signal sequence, calculating estimators of first-order parameters and outputting the estimators.

Description

technical field [0001] The invention belongs to the technical field of non-stationary signal analysis, and relates to a parameterized estimation method of non-stationary signals, in particular to a high-order polynomial phase signal parameter estimation method based on a reduced-order kernel function, which can be used for radar echo signals of maneuvering targets Detection and estimation and ISAR imaging technology and other fields. Background technique [0002] Polynomial phase signals (PPS) have been widely used in modeling non-stationary signals such as radar (Pulse Doppler radar, SAR and ISAR), sonar, communication, biomedicine, seismic analysis and animal acoustics applications. Linearity, Gaussian and stationary are the main aspects of traditional signal processing. Modern signal processing is characterized by nonlinear, non-Gaussian and non-stationary signals. In the study of non-stationary signals, polynomial phase signals are relatively common. The problem of ti...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06F17/14G06F17/15G01S7/40
CPCG01S7/40G06F17/142G06F17/156
Inventor 李明孙浩曹润清左磊吴艳
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com